What Is 1 1 2 Cups Divided By 4
Kalali
Aug 26, 2025 · 5 min read
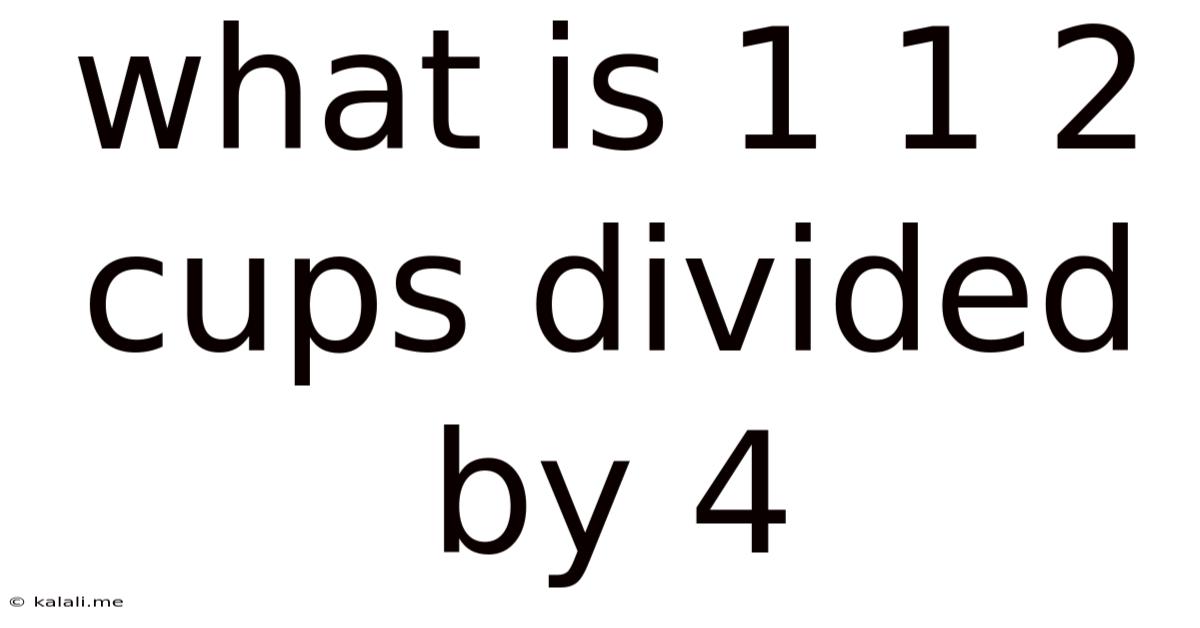
Table of Contents
What is 1 1/2 Cups Divided by 4? A Comprehensive Guide to Fraction Division in Baking and Beyond
This seemingly simple question – "What is 1 1/2 cups divided by 4?" – actually touches upon several important mathematical concepts relevant to everyday life, particularly in cooking and baking. Understanding how to solve this problem not only provides the answer but also reinforces fundamental skills in fraction manipulation and division. This guide will delve into the various methods of solving this problem, exploring the underlying principles and offering practical applications beyond the realm of culinary arts.
Meta Description: Learn how to divide fractions with ease! This comprehensive guide explains how to solve "1 1/2 cups divided by 4," detailing various methods and highlighting practical applications in baking and beyond. Master fraction division and improve your culinary skills.
Understanding the Problem: 1 1/2 Cups ÷ 4
The problem presented, 1 1/2 cups divided by 4, requires us to divide a mixed number (1 1/2) by a whole number (4). This is a common scenario in baking recipes where you need to scale down a recipe to yield fewer servings. Understanding how to accurately divide fractions is crucial for maintaining the correct proportions and achieving desired results.
Method 1: Converting to Improper Fractions
The most straightforward method involves converting the mixed number (1 1/2) into an improper fraction. An improper fraction has a numerator larger than or equal to its denominator.
-
Convert the mixed number: To convert 1 1/2 to an improper fraction, we multiply the whole number (1) by the denominator (2) and add the numerator (1). This sum becomes the new numerator, while the denominator remains the same.
1 1/2 = (1 * 2 + 1) / 2 = 3/2
-
Divide the fractions: Now, we have the problem 3/2 ÷ 4. To divide fractions, we multiply the first fraction by the reciprocal of the second fraction. The reciprocal of a number is simply 1 divided by that number. The reciprocal of 4 is 1/4.
3/2 ÷ 4 = 3/2 * 1/4
-
Multiply the numerators and denominators: Multiply the numerators together and the denominators together.
(3 * 1) / (2 * 4) = 3/8
Therefore, 1 1/2 cups divided by 4 is 3/8 of a cup.
Method 2: Dividing the Whole Number and Fraction Separately
This method is particularly intuitive and helpful for visualizing the process. We will divide the whole number and the fractional part separately and then combine the results.
-
Divide the whole number: Divide the whole number part of the mixed number (1) by 4.
1 ÷ 4 = 1/4
-
Divide the fractional part: Divide the fractional part (1/2) by 4. This is equivalent to multiplying 1/2 by 1/4.
1/2 ÷ 4 = 1/2 * 1/4 = 1/8
-
Combine the results: Add the results from steps 1 and 2.
1/4 + 1/8 = 2/8 + 1/8 = 3/8
Again, we arrive at the answer: 3/8 of a cup.
Method 3: Using Decimal Representation
While fractions are generally preferred in baking recipes for accuracy, we can also solve this using decimal representation.
-
Convert to decimals: Convert 1 1/2 to its decimal equivalent: 1.5
-
Divide the decimals: Divide 1.5 by 4.
1.5 ÷ 4 = 0.375
-
Convert back to a fraction (optional): To convert 0.375 back to a fraction, we can write it as 375/1000. Simplifying this fraction by dividing both the numerator and denominator by their greatest common divisor (125) gives us 3/8.
This method confirms our previous answer: 3/8 of a cup.
Practical Applications in Baking and Cooking
Understanding fraction division is vital for scaling recipes up or down. Imagine you have a cake recipe that calls for 1 1/2 cups of flour but you only want to bake half the recipe. You would divide 1 1/2 cups by 2 (not 4, in this case), resulting in 3/4 cup of flour. This precise measurement ensures the baked good retains its desired texture and flavor.
Beyond baking, this skill is useful in various culinary situations:
- Adjusting recipes for different serving sizes: Scaling a recipe for a smaller or larger group of people often involves dividing or multiplying ingredient quantities, frequently requiring fraction manipulation.
- Working with smaller measuring cups: If you don't have a measuring cup that precisely measures 3/8 of a cup, you can use a smaller measuring cup and repeat the measurement several times (e.g., using a 1/8 cup measuring cup three times).
- Understanding ingredient ratios: Many recipes express ingredients in ratios, and understanding how to divide and manipulate fractions helps to calculate the exact amounts needed.
Beyond the Kitchen: Real-World Applications
The ability to divide fractions isn't limited to cooking. It finds applications in numerous real-world scenarios:
- Construction and engineering: Calculating material quantities for projects often involves dividing fractions to determine precise amounts.
- Sewing and crafting: Adjusting patterns or calculating fabric requirements might necessitate dividing fractional measurements.
- Finance and budgeting: Dividing fractional shares of stocks or calculating portions of expenses frequently utilizes fraction division.
- Data analysis and statistics: Many statistical calculations and data representations involve fractions and their manipulation.
Mastering Fraction Division: Tips and Tricks
- Practice regularly: The best way to improve your skills is through consistent practice. Start with simple problems and gradually increase the complexity.
- Use visual aids: Drawing diagrams or using manipulatives (like fraction circles) can help visualize the division process.
- Utilize online calculators and resources: Many online tools can help you check your work and provide additional practice problems.
- Understand the underlying principles: Focusing on the fundamental concepts of fractions and reciprocal numbers will enhance your understanding and problem-solving abilities.
In conclusion, while seemingly simple, the problem of dividing 1 1/2 cups by 4 demonstrates the importance of understanding fraction division. This skill is not only valuable in the kitchen but also applicable to various aspects of life. By mastering the methods outlined above and practicing regularly, you can confidently tackle fraction division problems and apply this essential skill to various situations. Remember, understanding the "why" behind the mathematical processes is as important as knowing the "how," allowing for better problem-solving and a deeper appreciation of mathematics' relevance in our daily lives.
Latest Posts
Latest Posts
-
How Much Is 80 Kilometers In Miles
Aug 26, 2025
-
What Number Is One Hundred More Than 890
Aug 26, 2025
-
Which Of The Following Best Describes A Plane
Aug 26, 2025
-
How To Do Negative Exponents On Ti 30xa
Aug 26, 2025
-
What Is The Clasp Of A Necklace Called Boob
Aug 26, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 1 2 Cups Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.