What Is 1 1/4 + 1 1/4
Kalali
Aug 05, 2025 · 5 min read
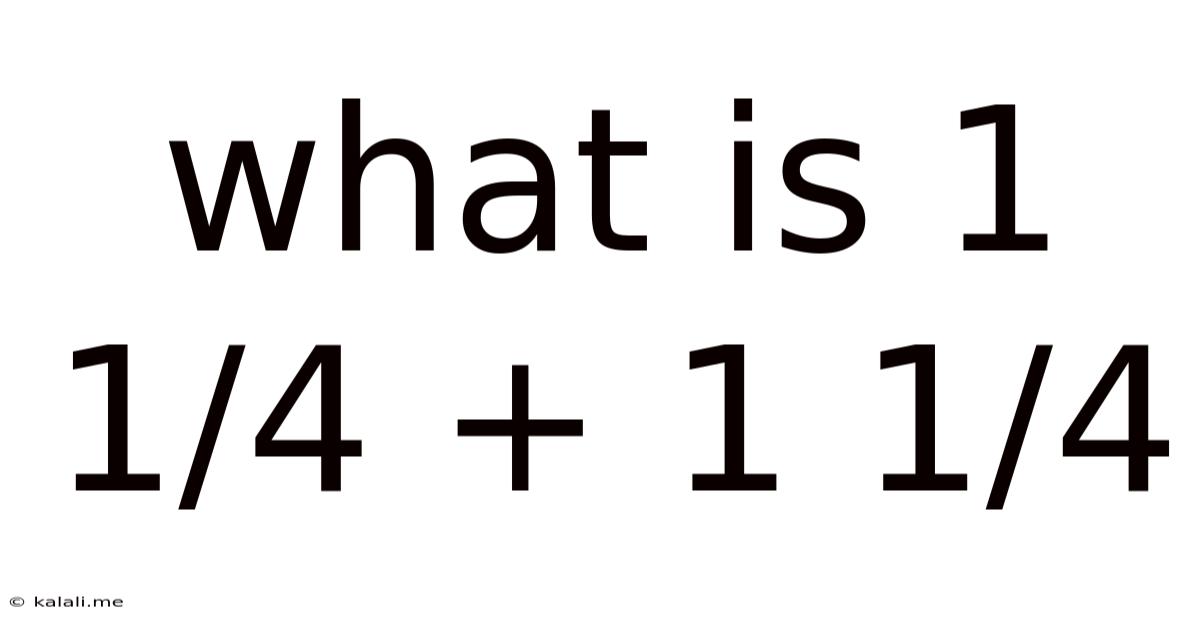
Table of Contents
Decoding 1 1/4 + 1 1/4: A Deep Dive into Fraction Addition and its Real-World Applications
This seemingly simple addition problem, 1 1/4 + 1 1/4, serves as a gateway to understanding fundamental mathematical concepts. While the answer might seem obvious at first glance, exploring the methods of solving it unlocks a broader understanding of fractions, mixed numbers, and their practical applications in everyday life. This article will not only provide the solution but also delve into the various approaches to solving this problem, highlighting the importance of fractional arithmetic and its relevance in various fields.
Meta Description: Learn how to solve 1 1/4 + 1 1/4, understanding the process of adding mixed numbers, and exploring practical applications of fraction addition in everyday scenarios. Discover multiple methods and gain a deeper understanding of fractional arithmetic.
Understanding Fractions and Mixed Numbers
Before tackling the problem, let's establish a firm understanding of the components: fractions and mixed numbers. A fraction represents a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many parts make up the whole. For example, in the fraction 1/4, the numerator is 1 and the denominator is 4, representing one out of four equal parts.
A mixed number combines a whole number and a fraction. In our problem, 1 1/4 is a mixed number, indicating one whole unit plus one-quarter of another unit. Understanding mixed numbers is crucial for solving addition problems involving fractions.
Method 1: Converting Mixed Numbers to Improper Fractions
One common method for adding mixed numbers involves converting them into improper fractions. An improper fraction has a numerator larger than or equal to its denominator. To convert 1 1/4 to an improper fraction, we multiply the whole number (1) by the denominator (4), add the numerator (1), and keep the same denominator. This gives us:
(1 * 4) + 1 = 5
Therefore, 1 1/4 is equivalent to 5/4.
Now, we can easily add the improper fractions:
5/4 + 5/4 = 10/4
This improper fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 2:
10/4 = 5/2
Finally, we convert the improper fraction 5/2 back into a mixed number:
5 divided by 2 is 2 with a remainder of 1. Therefore, 5/2 = 2 1/2.
Therefore, 1 1/4 + 1 1/4 = 2 1/2.
Method 2: Adding the Whole Numbers and Fractions Separately
Another approach involves adding the whole numbers and the fractions separately. This method can be more intuitive for some individuals.
First, add the whole numbers: 1 + 1 = 2
Next, add the fractions: 1/4 + 1/4 = 2/4
Since 2/4 can be simplified to 1/2, we combine the whole number sum and the simplified fraction:
2 + 1/2 = 2 1/2
This method demonstrates the same result, highlighting the flexibility in approaching fraction addition problems.
Method 3: Visual Representation with Diagrams
Visual aids can be particularly helpful in understanding fraction addition, especially for beginners. Imagine two circles, each divided into four equal quarters. One circle has one quarter shaded, and the other circle also has one quarter shaded. In addition to these, each circle is completely shaded representing the whole number 1. Combining the shaded areas of both circles shows that we have two whole circles completely shaded plus two quarters shaded which is 2 1/2. This visual representation reinforces the concept of adding fractions and provides a concrete understanding of the result.
Real-World Applications of Fraction Addition
The ability to add fractions is not limited to theoretical mathematical exercises. It finds practical applications in numerous everyday situations:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Adding fractions is essential for accurately calculating the total quantity of ingredients needed when adjusting recipes or combining ingredients from multiple sources. For example, if a recipe calls for 1 1/4 cups of flour and you need to double the recipe, you'll need to calculate 1 1/4 + 1 1/4.
-
Construction and Measurement: Construction projects rely heavily on precise measurements. Carpenters, plumbers, and electricians frequently encounter situations where they need to add fractional measurements of lengths, widths, or volumes. Accurate calculations using fractions ensure that projects are completed according to specifications.
-
Finance and Budgeting: Understanding fractions is crucial for managing personal finances. Calculating portions of budgets, interest rates, or discounts often involves working with fractions. For instance, if you spend 1/4 of your income on rent and 1/4 on groceries, you need to add these fractions to understand the total portion of your income allocated to these expenses.
-
Time Management: Time is often measured in fractions of an hour or a day. Calculating total time spent on tasks or projects frequently involves adding fractions. For instance, if you spend 1 1/4 hours studying and 1 1/4 hours working, understanding fraction addition helps determine the total time spent.
-
Data Analysis: In many fields, data is presented in fractional or percentage forms. Adding fractions is essential for interpreting and analyzing this data effectively.
Beyond the Basics: Expanding on Fraction Addition
While this article focused on the simple addition of 1 1/4 + 1 1/4, understanding this fundamental operation opens doors to more complex calculations. This includes:
-
Adding fractions with different denominators: This requires finding a common denominator before adding the numerators.
-
Adding more than two fractions: The same principles apply; you can add multiple fractions by either converting to improper fractions or finding a common denominator.
-
Subtracting fractions: Similar methods are used for subtraction, with the main difference being the subtraction of numerators instead of addition.
-
Multiplying and dividing fractions: These operations have different rules and are essential for a comprehensive understanding of fractional arithmetic.
Conclusion
The seemingly simple problem of 1 1/4 + 1 1/4 provides a valuable foundation for understanding fractions, mixed numbers, and their applications in real-world scenarios. Mastering these basic concepts is crucial for success in various academic and professional fields. By employing different methods of calculation and understanding the underlying principles, one can confidently tackle more complex fractional arithmetic problems and apply this knowledge to solve practical challenges in everyday life. Remember that a solid grasp of fractional arithmetic is a fundamental building block for more advanced mathematical concepts and their applications.
Latest Posts
Latest Posts
-
How Many Square Feet In A Lot
Aug 07, 2025
-
Should I Wash My Hair Before A Perm
Aug 07, 2025
-
The Most Diverse Classical Music Period Was
Aug 07, 2025
-
1996 Chevy Silverado Radio Wiring Harness Diagram
Aug 07, 2025
-
How Many Eighths Are In A Quarter
Aug 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 1/4 + 1 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.