What Is 1 2 Of 1 5
Kalali
Jul 06, 2025 · 5 min read
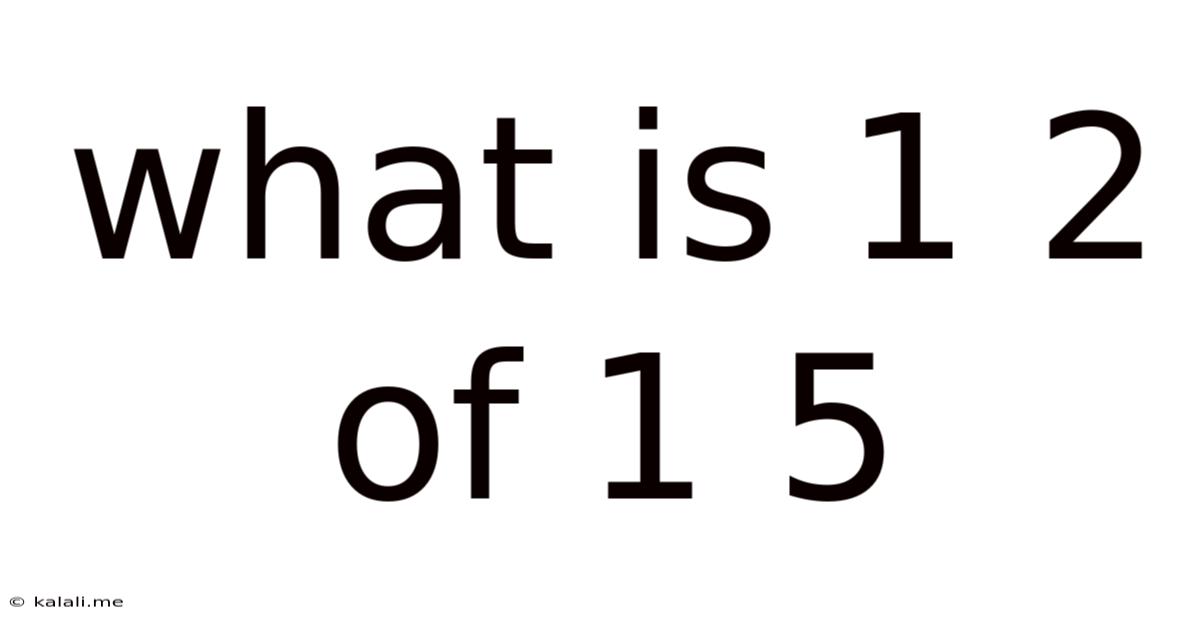
Table of Contents
What is 1/2 of 1/5? A Deep Dive into Fraction Multiplication and its Real-World Applications
This seemingly simple question, "What is 1/2 of 1/5?", opens the door to a deeper understanding of fraction multiplication, a fundamental concept in mathematics with widespread applications in various fields. This article will not only answer the question directly but also explore the underlying principles, provide practical examples, and delve into the reasoning behind the calculations. We'll even look at how this basic fractional operation finds its way into more complex scenarios. Understanding fraction multiplication is crucial for success in algebra, geometry, and even everyday tasks like cooking and construction.
Understanding Fractions: A Quick Refresher
Before we tackle the problem at hand, let's briefly review the concept of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 1/2, the numerator is 1, and the denominator is 2, representing one out of two equal parts.
Multiplying Fractions: The "Of" Means Multiplication
The phrase "1/2 of 1/5" directly translates into a multiplication problem: (1/2) * (1/5). Multiplying fractions is a straightforward process:
- Multiply the numerators: Multiply the top numbers together. In this case, 1 * 1 = 1.
- Multiply the denominators: Multiply the bottom numbers together. In this case, 2 * 5 = 10.
- Combine the results: The resulting fraction is the product of the numerators over the product of the denominators. Therefore, (1/2) * (1/5) = 1/10.
Therefore, 1/2 of 1/5 is 1/10.
Visualizing Fraction Multiplication
Visual representations can make abstract concepts like fraction multiplication easier to grasp. Imagine a rectangular cake. If we divide the cake into five equal pieces, then 1/5 of the cake represents one of those pieces. Now, if we take half (1/2) of that 1/5 piece, we're left with a smaller portion. This smaller portion represents 1/10 of the original cake.
Real-World Applications of Fraction Multiplication
Fraction multiplication isn't just an abstract mathematical concept; it's frequently used in everyday life:
- Cooking: If a recipe calls for 1/2 a cup of flour, and you want to make only 1/5 of the recipe, you'll need to calculate 1/2 * 1/5 = 1/10 of a cup of flour.
- Construction: If a project requires 1/5 of a roll of wire, and you only need 1/2 of that amount, you'll use 1/10 of a roll.
- Finance: Calculating interest, discounts, or portions of a budget often involves fraction multiplication. For example, if you receive 1/5 of your annual bonus in each quarter, and you want to save 1/2 of one quarterly payment, you will save 1/10 of your total bonus.
- Gardening: If you need to use 1/5 of a bag of fertilizer for your garden, and you decide to use only 1/2 of that amount today, you will use 1/10 of the bag today.
Extending the Concept: Multiplying Fractions with Larger Numbers
The principle remains the same even when dealing with larger numbers in the numerator and denominator. For example, let's calculate 3/4 of 2/7:
- Multiply the numerators: 3 * 2 = 6
- Multiply the denominators: 4 * 7 = 28
- Combine the results: The answer is 6/28.
This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator, which is 2. Dividing both the numerator and denominator by 2, we simplify 6/28 to 3/14.
Simplifying Fractions: A Crucial Step
Simplifying fractions is essential for presenting results in their most concise and understandable form. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator and divide both by the GCD. This process ensures that the fraction is expressed in its lowest terms.
Mixed Numbers and Fraction Multiplication
A mixed number combines a whole number and a fraction (e.g., 1 1/2). To multiply fractions involving mixed numbers, first convert the mixed numbers into improper fractions. An improper fraction is one where the numerator is greater than or equal to the denominator. For example, 1 1/2 is converted to 3/2 (by multiplying the whole number by the denominator and adding the numerator, keeping the same denominator).
Let's calculate 1 1/2 * 2/5:
- Convert to improper fractions: 1 1/2 becomes 3/2.
- Multiply the fractions: (3/2) * (2/5) = 6/10
- Simplify the fraction: 6/10 simplifies to 3/5.
Therefore, 1 1/2 of 2/5 is 3/5.
Solving More Complex Problems Involving Fractions
The principles discussed above can be extended to solve more complex problems involving multiple fractions and operations. For example, consider the following problem:
(1/2 + 1/4) * (2/3 - 1/6)
First, solve the operations within the parentheses:
- 1/2 + 1/4 = 3/4 (finding a common denominator)
- 2/3 - 1/6 = 3/6 = 1/2 (finding a common denominator and simplifying)
Now, multiply the resulting fractions:
(3/4) * (1/2) = 3/8
Therefore, (1/2 + 1/4) * (2/3 - 1/6) = 3/8.
Applications in Advanced Mathematics
Fraction multiplication is a foundational concept that extends into more advanced mathematical areas:
- Algebra: Solving equations and simplifying algebraic expressions often involves manipulating fractions.
- Calculus: Derivatives and integrals frequently involve operations with fractions and fractional exponents.
- Geometry: Calculating areas, volumes, and proportions of shapes often requires the use of fractions.
- Probability and Statistics: Calculating probabilities and interpreting statistical data frequently involves working with fractions and ratios.
Conclusion
The simple question "What is 1/2 of 1/5?" has provided a springboard for a comprehensive exploration of fraction multiplication. This fundamental mathematical operation, seemingly straightforward at first glance, underpins a vast array of applications across numerous disciplines, from everyday tasks to advanced mathematical concepts. Mastering fraction multiplication is not just about memorizing procedures but also about understanding the underlying principles and visualizing the concept to build a strong mathematical foundation. By understanding and practicing these concepts, you can confidently tackle more complex mathematical problems and apply this knowledge to solve real-world challenges. The ability to work fluently with fractions is a valuable skill that will serve you well throughout your academic and professional life.
Latest Posts
Latest Posts
-
How Many Laps Is 500 Yards In A Pool
Jul 31, 2025
-
What Is A 17 Out Of 23
Jul 31, 2025
-
3 Liter Of Water How Many Glasses
Jul 31, 2025
-
5 Letter Words With 2nd Letter I
Jul 31, 2025
-
What Is The Color Of A Starfish
Jul 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2 Of 1 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.