What Is 1 3 Of 100
Kalali
Apr 13, 2025 · 5 min read
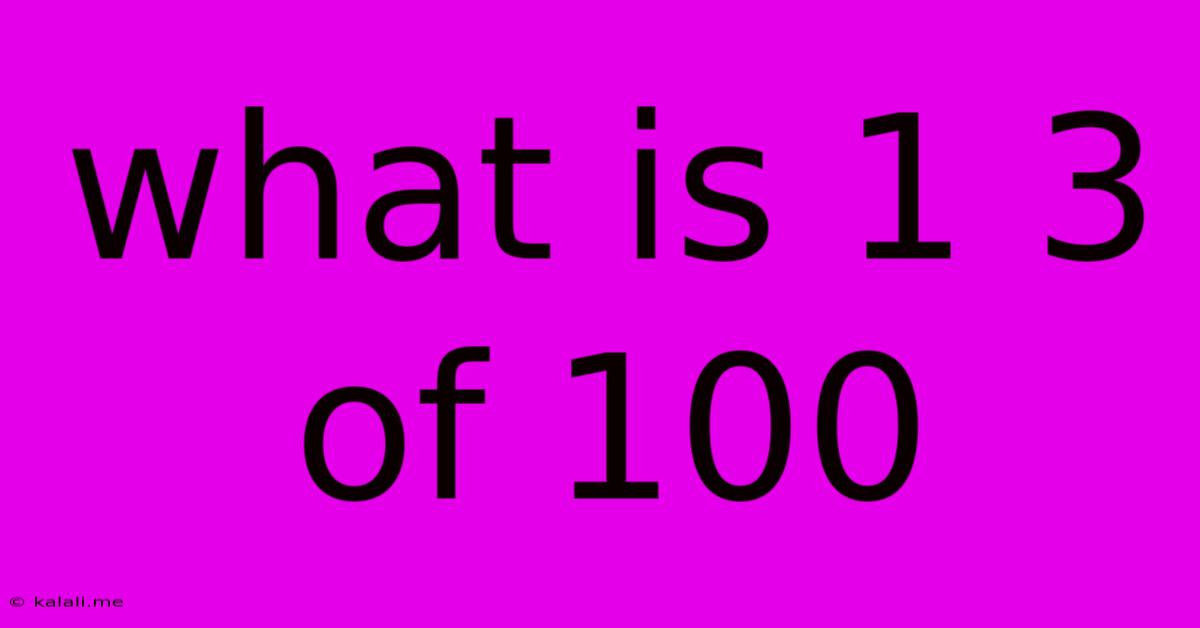
Table of Contents
What is 1/3 of 100? A Comprehensive Guide to Fractions and Their Applications
Finding one-third of 100 might seem like a simple arithmetic problem, but understanding the underlying concepts of fractions and their applications can unlock a world of mathematical possibilities. This comprehensive guide dives deep into solving this seemingly simple question, exploring the various methods, underlying principles, and real-world applications of fractional calculations. We'll cover everything from basic fraction arithmetic to more advanced concepts, ensuring you gain a thorough understanding of this fundamental mathematical operation.
Meta Description: Learn how to calculate 1/3 of 100 and explore the world of fractions. This comprehensive guide covers various methods, applications, and related concepts, making fraction calculations easy to understand.
What is 1/3 of 100? The Simple Solution
The most straightforward way to calculate 1/3 of 100 is to perform the following calculation:
(1/3) * 100 = 100/3 = 33.333...
Therefore, one-third of 100 is approximately 33.33. The result is a recurring decimal, meaning the '3' after the decimal point repeats infinitely. For practical purposes, rounding to two decimal places is usually sufficient.
However, this simple answer only scratches the surface. Let's delve deeper into the world of fractions to understand the "why" behind the calculation.
Understanding Fractions: A Building Block of Mathematics
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into. In our case, 1/3 represents one part out of three equal parts.
Methods for Calculating 1/3 of 100
While simple multiplication provides the direct answer, let's explore other methods to reinforce understanding:
-
Division: Dividing 100 by 3 achieves the same result: 100 ÷ 3 ≈ 33.33. This method highlights the relationship between fractions and division; a fraction can be interpreted as a division problem.
-
Long Division: Performing long division manually provides a step-by-step understanding of how the decimal value is derived. This reinforces the concept of dividing the whole (100) into equal parts (3).
-
Visual Representation: Imagine a circle divided into three equal parts. Shading one of those parts visually represents 1/3. Scaling this representation to represent 100 units total can help visualize the approximate value of 1/3 of 100.
-
Percentage Conversion: Converting the fraction 1/3 to a percentage provides an alternative perspective. 1/3 is approximately 33.33%, so finding 33.33% of 100 yields the same answer. This method highlights the interconnectedness between fractions, decimals, and percentages.
Real-World Applications of Fractional Calculations
Understanding fractions isn't just about solving math problems; it's crucial for numerous real-world applications:
-
Cooking and Baking: Recipes often involve fractional measurements. Calculating 1/3 of a cup of flour or 2/3 of a teaspoon of baking powder requires understanding fractional proportions.
-
Construction and Engineering: Precise measurements and calculations are essential. Fractions are used in blueprint readings, material estimations, and the precise cutting of materials.
-
Finance and Budgeting: Fractions are used extensively in finance. Calculating interest rates, understanding loan payments, and analyzing investment returns all involve fractional calculations.
-
Data Analysis and Statistics: Fractions are fundamental to statistical calculations, such as calculating proportions, percentages, and probabilities. Understanding fractions is essential for interpreting data effectively.
-
Science and Measurement: Scientific measurements often involve fractions and decimals. Precision and accuracy in scientific calculations depend on a solid understanding of fractional relationships.
Beyond the Basics: Expanding Our Understanding of Fractions
While calculating 1/3 of 100 provides a foundational understanding, let's explore some related concepts:
-
Improper Fractions and Mixed Numbers: An improper fraction is where the numerator is larger than the denominator (e.g., 100/3). A mixed number combines a whole number and a proper fraction (e.g., 33 1/3). Understanding the conversion between these forms is essential for more complex calculations.
-
Equivalent Fractions: Different fractions can represent the same value (e.g., 1/3, 2/6, 3/9). Identifying equivalent fractions simplifies calculations and allows for easier comparisons.
-
Adding and Subtracting Fractions: Combining or subtracting fractions requires finding a common denominator. This skill is essential for more intricate fractional calculations.
-
Multiplying and Dividing Fractions: These operations have unique rules that differ from whole-number arithmetic. Mastering these rules is crucial for solving complex problems.
Addressing Common Mistakes and Challenges
Many common mistakes arise when working with fractions. Addressing these proactively ensures accurate calculations:
-
Incorrectly applying the order of operations: Remember PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction).
-
Errors in simplifying fractions: Always simplify fractions to their lowest terms to make calculations easier and results clearer.
-
Confusing numerator and denominator: Always double-check that you're using the correct numbers in the correct positions.
-
Rounding errors: Be mindful of rounding errors, especially when dealing with recurring decimals.
Advanced Applications and Extensions
The concept of finding a fraction of a number extends to more complex scenarios:
-
Finding fractions of larger numbers: The same principles apply when dealing with larger numbers. Understanding the underlying logic remains consistent.
-
Calculating fractions of fractions: This involves multiplying fractions, requiring understanding of fraction multiplication rules.
-
Using fractions in algebraic equations: Fractions appear in various algebraic expressions and equations, requiring an understanding of algebraic manipulation.
Conclusion: Mastering Fractions for a Brighter Future
While the seemingly simple question, "What is 1/3 of 100?" might appear trivial at first glance, it serves as a gateway to understanding the broader world of fractions. Mastering fraction calculations is not only essential for academic success but also invaluable in navigating the complexities of the real world. From everyday tasks like cooking to complex calculations in engineering and finance, understanding fractions empowers you with the tools to solve problems effectively and efficiently. By grasping the underlying concepts and practicing regularly, you can confidently tackle any fractional calculation that comes your way, paving the path for future mathematical success and a deeper understanding of the world around you. Remember that continued practice and exploration of related concepts are key to truly mastering this fundamental aspect of mathematics.
Latest Posts
Latest Posts
-
40 Oz Of Water Is How Many Cups
Jul 18, 2025
-
How Many Eighths In A Quarter Pound
Jul 18, 2025
-
Can The Sine Of An Angle Ever Equal 2
Jul 18, 2025
-
How Many Months Is A Hundred Days
Jul 18, 2025
-
Mother And I Or Mother And Me
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 3 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.