What Is 1.4 As A Percent
Kalali
Apr 01, 2025 · 5 min read
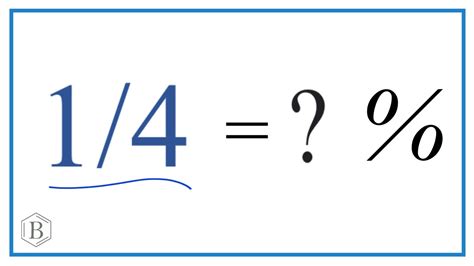
Table of Contents
What is 1.4 as a Percent? A Comprehensive Guide
Converting decimals to percentages is a fundamental skill in mathematics with wide-ranging applications in various fields, from finance and statistics to everyday life. Understanding this conversion process is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This article provides a comprehensive guide on how to convert 1.4 to a percentage, explores the underlying concepts, and offers practical examples to solidify your understanding.
Understanding Decimals and Percentages
Before diving into the conversion of 1.4, let's briefly revisit the definitions of decimals and percentages.
-
Decimals: Decimals represent fractional parts of a whole number. They use a decimal point to separate the whole number part from the fractional part. For example, in 1.4, '1' represents the whole number, and '.4' represents four-tenths (4/10).
-
Percentages: Percentages represent a fraction of 100. The symbol "%" denotes "per cent," meaning "out of one hundred." Therefore, 50% signifies 50 out of 100, which is equivalent to 50/100 or 0.5 as a decimal.
Converting 1.4 to a Percentage: The Method
The conversion from a decimal to a percentage involves multiplying the decimal by 100 and adding the percentage symbol. Here's how it works for 1.4:
-
Multiply by 100: 1.4 x 100 = 140
-
Add the Percentage Symbol: 140%
Therefore, 1.4 as a percent is 140%.
Why is 1.4 More Than 100%?
The result of 140% might seem counterintuitive at first glance. Most people associate percentages with values between 0% and 100%. However, percentages can exceed 100%. This simply means that the value represents more than the whole. In this case, 1.4 signifies 140% of 1. It's 100% of 1 (which is 1) plus an additional 40% of 1 (which is 0.4).
Think of it like this: If you had 100 apples and you increased your number of apples by 40%, you would now have 140 apples. This demonstrates how percentages can easily exceed 100%.
Real-World Applications of Percentages Exceeding 100%
Percentages greater than 100% frequently appear in various contexts:
-
Finance: Investment growth, return on investment (ROI), and profit margins often exceed 100%. For instance, a 150% return on investment indicates that the investment doubled and generated an additional 50% profit.
-
Economics: Economic growth rates, population increases, and inflation rates can also exceed 100%. A 120% increase in GDP implies that the gross domestic product grew by more than double its original size.
-
Statistics: Data analysis sometimes uses percentages exceeding 100% to show significant changes or trends. For example, comparing the present value to a past value might yield a percentage greater than 100%.
-
Science: Scientific measurements and calculations often involve percentages that surpass 100%, particularly in areas like chemical reactions and population studies.
Further Examples of Decimal to Percentage Conversions
To enhance your understanding, let's explore a few more examples of decimal-to-percentage conversions:
- 0.5: 0.5 x 100 = 50%
- 0.75: 0.75 x 100 = 75%
- 2.5: 2.5 x 100 = 250%
- 0.05: 0.05 x 100 = 5%
- 10.2: 10.2 x 100 = 1020%
Converting Percentages to Decimals: The Reverse Process
The reverse process, converting percentages to decimals, is equally important. This involves dividing the percentage by 100 and removing the percentage symbol.
For example, to convert 140% back to a decimal:
-
Remove the Percentage Symbol: 140
-
Divide by 100: 140 / 100 = 1.4
This confirms our initial conversion.
Practical Applications and Problem Solving
Let's consider a few practical problems to illustrate the application of decimal-to-percentage conversion:
Problem 1: A company's revenue increased from $1 million to $1.4 million. What is the percentage increase in revenue?
Solution: The increase in revenue is $1.4 million - $1 million = $0.4 million. To express this as a percentage of the original revenue, we divide the increase by the original revenue and multiply by 100: ($0.4 million / $1 million) x 100 = 40%. Therefore, the company's revenue increased by 40%.
Problem 2: A student scored 1.4 times the average score on a test. Express this as a percentage.
Solution: 1.4 x 100 = 140%. The student scored 140% of the average score.
Problem 3: A product's price increased by 140%. If the original price was $50, what is the new price?
Solution: The increase in price is 140% of $50 = (140/100) x $50 = $70. The new price is the original price plus the increase: $50 + $70 = $120.
Mastering Percentage Conversions: Tips and Tricks
Here are some helpful tips for mastering decimal-to-percentage conversions:
-
Practice Regularly: Consistent practice is key to developing fluency in converting decimals to percentages and vice versa.
-
Use Visual Aids: Diagrams, charts, and other visual aids can make the concept more intuitive and easier to grasp.
-
Real-world Application: Apply your knowledge to real-world scenarios to reinforce understanding and improve problem-solving skills.
-
Check your Work: Always double-check your calculations to ensure accuracy.
-
Utilize Online Resources: Numerous online calculators and tutorials are available to help you practice and learn.
Conclusion: The Significance of Percentage Conversions
Understanding how to convert decimals to percentages is a fundamental skill with far-reaching applications in numerous fields. The ability to accurately and efficiently perform these conversions is essential for interpreting data, making informed decisions, and effectively communicating numerical information. This article has explored the concept comprehensively, providing practical examples and techniques to solidify your understanding of this crucial mathematical skill. Mastering percentage conversions will empower you to analyze data more effectively and navigate numerical information with greater confidence. Remember that percentages exceeding 100% are perfectly valid and represent values greater than the whole. By understanding this, you can confidently interpret and apply this knowledge in various real-world contexts.
Latest Posts
Latest Posts
-
105 Out Of 120 As A Percentage
Apr 02, 2025
-
How Many Ml Is 1 4 Oz
Apr 02, 2025
-
How Many Centimeters Is 23 Inches
Apr 02, 2025
-
How Many Gallons Is 10 Cups
Apr 02, 2025
-
What Is 62 Degrees Celsius In Fahrenheit
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 1.4 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
