What Is 1 4 Divided By 1 3
Kalali
Jul 22, 2025 · 5 min read
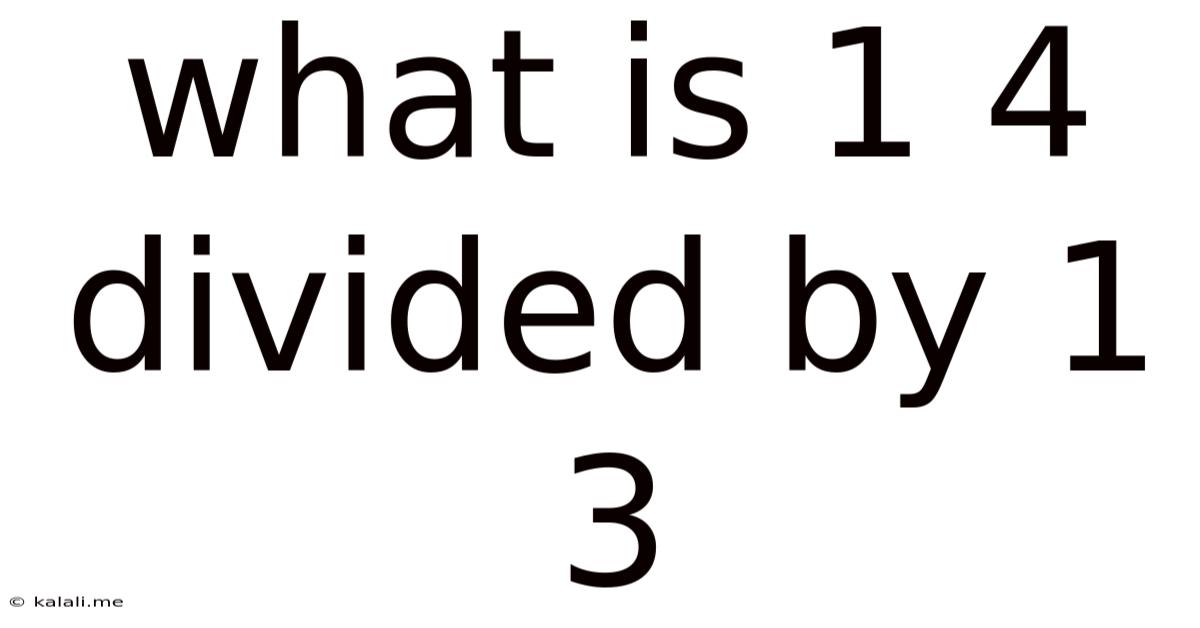
Table of Contents
What is 1 ¼ Divided by 1 ⅓? A Deep Dive into Fraction Division
This article will comprehensively explore the seemingly simple question: "What is 1 ¼ divided by 1 ⅓?". While the calculation itself is straightforward, understanding the underlying principles of fraction division offers valuable insights into mathematical operations and problem-solving. We'll not only solve the problem but also delve into the various methods for tackling fraction division, emphasizing the importance of understanding the "why" behind the calculations. This will help you confidently handle similar problems in the future, enhancing your mathematical skills and understanding.
Understanding Fractions: A Quick Refresher
Before jumping into the division, let's briefly refresh our understanding of fractions. A fraction represents a part of a whole, consisting of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction ⅓, the numerator is 1 and the denominator is 3, meaning we have 1 out of 3 equal parts.
Converting Mixed Numbers to Improper Fractions
Our problem involves mixed numbers (numbers containing both a whole number and a fraction), specifically 1 ¼ and 1 ⅓. To simplify the division process, it's crucial to convert these mixed numbers into improper fractions. An improper fraction has a numerator larger than or equal to its denominator.
-
Converting 1 ¼: To convert 1 ¼ to an improper fraction, we multiply the whole number (1) by the denominator (4) and add the numerator (1). This result becomes the new numerator, while the denominator remains the same. Therefore, 1 ¼ becomes (1 x 4) + 1 / 4 = ⁵⁄₄.
-
Converting 1 ⅓: Similarly, for 1 ⅓, we calculate (1 x 3) + 1 / 3 = ⁴⁄₃.
Now our problem becomes: ⁵⁄₄ ÷ ⁴⁄₃.
Methods for Dividing Fractions
There are two primary methods for dividing fractions:
-
The "Keep, Change, Flip" Method: This is the most common and arguably the easiest method. It involves:
- Keeping the first fraction as it is (⁵⁄₄).
- Changing the division sign (÷) to a multiplication sign (x).
- Flipping (or finding the reciprocal of) the second fraction (⁴⁄₃ becomes ³⁄₄).
Therefore, the problem becomes: ⁵⁄₄ x ³⁄₄.
-
The Common Denominator Method: This method involves finding a common denominator for both fractions, converting them to equivalent fractions with the same denominator, and then dividing the numerators. While less commonly used for simple divisions, understanding this method provides a deeper understanding of fraction manipulation.
Let's apply both methods to solve our problem:
Method 1: Keep, Change, Flip
⁵⁄₄ x ³⁄₄ = (5 x 3) / (4 x 4) = ¹⁵⁄₁₆
Therefore, 1 ¼ divided by 1 ⅓ equals ¹⁵⁄₁₆.
Method 2: Common Denominator
This method requires a slightly more complex approach for this specific problem, making the "Keep, Change, Flip" method more efficient. However, let's illustrate the principle:
-
Find the least common denominator (LCD): The LCD of 4 and 3 is 12.
-
Convert the fractions to equivalent fractions with the LCD:
- ⁵⁄₄ = ¹⁵⁄₁₂ (multiply numerator and denominator by 3)
- ⁴⁄₃ = ¹⁶⁄₁₂ (multiply numerator and denominator by 4)
-
Rewrite the division problem: ¹⁵⁄₁₂ ÷ ¹⁶⁄₁₂
-
Divide the numerators: This step is where the confusion might arise. When dividing fractions with the same denominator, we can divide the numerators, but the result is not intuitive for beginners.
-
Interpreting the result: The result of ¹⁵⁄₁₂ ÷ ¹⁶⁄₁₂ is not directly obvious like in the "Keep, Change, Flip" method. It's more helpful to think of it in terms of how many times ¹⁶⁄₁₂ goes into ¹⁵⁄₁₂ which logically isn't a whole number. To resolve it using the common denominator method directly would require additional steps to convert this back into a fraction and then simplify. It's this complexity that makes the "Keep, Change, Flip" method preferable for most fraction division problems.
Simplifying the Result and Understanding the Answer
Our answer, ¹⁵⁄₁₆, is an improper fraction. While it's perfectly acceptable to leave the answer in this form, we can also convert it back to a mixed number for better understanding:
15 divided by 16 is 0 with a remainder of 15. Therefore, ¹⁵⁄₁₆ can be expressed as 0 ¹⁵⁄₁₆. This means that 1 ¼ is slightly less than 1 ⅓, hence the result is less than 1.
Real-World Applications of Fraction Division
Understanding fraction division isn't just about solving textbook problems; it has numerous practical applications in various fields:
-
Cooking and Baking: Scaling recipes up or down requires dividing or multiplying fractions. For example, if a recipe calls for 1 ¼ cups of flour and you want to make half the recipe, you would divide 1 ¼ by 2.
-
Construction and Engineering: Precise measurements in construction often involve fractions, and division is crucial for calculating material quantities or dividing spaces.
-
Sewing and Tailoring: Cutting fabric accurately necessitates working with fractions, and division is essential for pattern adjustments.
-
Data Analysis and Statistics: Many statistical calculations involve fractions, and understanding fraction division is crucial for interpreting data.
Beyond the Basics: Extending Your Knowledge
While we've focused on a specific problem, the principles discussed extend to more complex fraction division involving multiple fractions, decimals, and even algebraic expressions. Mastering the fundamentals of fraction division is the cornerstone of further mathematical exploration. To solidify your understanding, practice solving various fraction division problems, experimenting with both methods.
Conclusion: Mastering Fraction Division for Mathematical Fluency
This article has provided a thorough exploration of how to solve 1 ¼ divided by 1 ⅓, highlighting the importance of converting mixed numbers to improper fractions and the efficiency of the "Keep, Change, Flip" method. Understanding fraction division is fundamental to mathematical fluency, extending beyond simple calculations to real-world applications in various fields. By mastering these concepts, you equip yourself with valuable problem-solving skills applicable across numerous disciplines. Remember to practice regularly and don't hesitate to explore more complex problems to deepen your understanding and build confidence in your mathematical abilities. The more you practice, the more intuitive and effortless fraction division will become.
Latest Posts
Latest Posts
-
What Company Has Most 6 Figure Earners
Jul 22, 2025
-
How Many Ounces Are In 2 Tons
Jul 22, 2025
-
How Many Slices Of Ham In A Pound
Jul 22, 2025
-
How Many Popcorn Kernels In A Cup
Jul 22, 2025
-
What Channels Are The Music Channels On Dish Network
Jul 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 4 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.