What Is 1 Percent Of 12
Kalali
Apr 10, 2025 · 5 min read
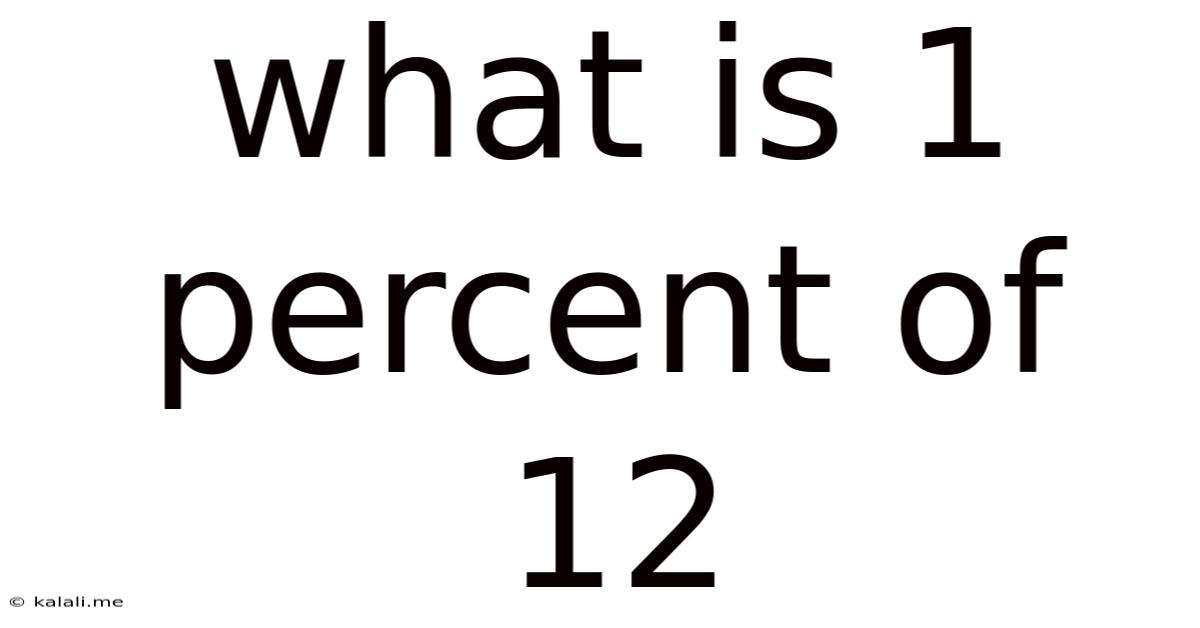
Table of Contents
What is 1 Percent of 12? A Deep Dive into Percentages and Their Applications
What is 1 percent of 12? The answer is simple: 0.12. But this seemingly straightforward calculation opens the door to a world of mathematical concepts, practical applications, and even surprising real-world implications. This article delves beyond the simple answer, exploring the fundamental principles of percentages, demonstrating various methods for calculating 1% of 12, and showcasing the relevance of percentage calculations in diverse fields. We'll also touch upon common pitfalls and provide practical tips to improve your understanding and application of percentages.
Understanding Percentages: A Foundation for Calculation
Before diving into the specifics of calculating 1% of 12, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The term "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 1% represents 1 part out of 100 equal parts. This fundamental understanding is crucial for accurately interpreting and utilizing percentages in various contexts.
Methods for Calculating 1% of 12
There are several approaches to calculating 1% of 12, each offering a slightly different perspective on the underlying mathematical principles.
1. The Direct Method: Using the Percentage Formula
The most straightforward method involves using the basic percentage formula:
(Percentage/100) * Whole Number = Result
In our case:
(1/100) * 12 = 0.12
This method is highly intuitive and easily applicable to various percentage calculations. It emphasizes the direct relationship between the percentage, the whole number, and the resulting part.
2. The Decimal Method: Converting Percentage to Decimal
This method involves converting the percentage into its decimal equivalent before performing the calculation. Since 1% is equal to 0.01, the calculation becomes:
0.01 * 12 = 0.12
This method highlights the equivalence between percentages and decimals, which is essential for advanced calculations and working with spreadsheets or programming languages.
3. The Fraction Method: Representing Percentage as a Fraction
We can also represent 1% as a fraction: 1/100. The calculation then becomes:
(1/100) * 12 = 12/100 = 0.12
This method underscores the fundamental relationship between percentages, decimals, and fractions, reinforcing the underlying mathematical concepts.
4. The Proportion Method: Setting up a Proportion
This method involves setting up a proportion to solve for the unknown value. We can set up the following proportion:
1/100 = x/12
Solving for x, we get:
x = (1 * 12) / 100 = 0.12
This method showcases the proportional relationship between the percentage and the whole number, providing a more formal mathematical approach to the calculation.
Applications of Percentage Calculations: Beyond the Basics
While the calculation of 1% of 12 might seem trivial, the underlying principles of percentage calculations have far-reaching applications across numerous fields:
-
Finance: Percentages are fundamental in finance, used for calculating interest rates, returns on investments (ROI), profit margins, discounts, taxes, and much more. Understanding percentage calculations is crucial for making informed financial decisions. For example, calculating the interest accrued on a loan or the discount on a sale item requires a solid grasp of percentage calculations. Analyzing financial statements also relies heavily on interpreting percentages, such as profit margins or debt-to-equity ratios.
-
Statistics: Percentages are extensively used in statistics to represent proportions, probabilities, and frequencies. For example, expressing survey results, analyzing data distributions, or calculating confidence intervals all rely on percentage calculations. Understanding these statistical concepts empowers us to critically evaluate information and make data-driven decisions.
-
Science: Scientific research utilizes percentages to represent experimental results, error margins, and changes in quantities. Reporting experimental outcomes often involves calculating percentage changes or representing data as percentages of a whole.
-
Everyday Life: Percentage calculations are integrated into our daily lives in various ways. Calculating tips in restaurants, understanding sales discounts, determining the nutritional content of food, or interpreting weather forecasts all involve working with percentages.
-
Business: Businesses use percentages for various purposes, including pricing strategies, calculating sales tax, determining profit margins, assessing market share, and analyzing performance metrics. Accurate percentage calculations are essential for effective business decision-making and financial planning.
-
Education: Percentages are a cornerstone of mathematics education, building a foundation for more advanced concepts and problem-solving skills. Mastering percentage calculations enhances analytical and problem-solving skills, applicable in various academic disciplines.
Common Pitfalls and Tips for Accuracy
Despite their apparent simplicity, percentage calculations can be prone to errors if not approached carefully. Common pitfalls include:
-
Incorrect Decimal Placement: Mistakes in converting percentages to decimals are a frequent source of error. Always double-check your decimal placement before performing any calculation.
-
Confusion with Whole Numbers and Parts: Understanding the distinction between the whole number and the part represented by the percentage is crucial. Misinterpreting which number represents the whole can lead to inaccurate results.
-
Using Incorrect Formulas: There are various formulas for different percentage calculations (e.g., calculating percentage increase or decrease). Using the wrong formula leads to incorrect results.
Tips for Accurate Percentage Calculations:
-
Double-check your calculations: Always verify your work to ensure accuracy.
-
Break down complex problems: For complex problems, break them down into smaller, manageable steps.
-
Use a calculator: Using a calculator reduces the chance of manual calculation errors.
-
Understand the context: Pay close attention to the context of the problem to ensure you are using the correct formula and interpreting the results correctly.
-
Practice regularly: The more you practice, the more comfortable and accurate you will become.
Conclusion: The Significance of a Simple Calculation
While the answer to "What is 1 percent of 12?" is a simple 0.12, the implications of understanding percentage calculations are far-reaching. Mastering these fundamental mathematical concepts provides the tools for navigating a wide range of situations, from personal finance to complex scientific research. By understanding the different methods of calculation and avoiding common pitfalls, you can confidently tackle percentage problems and utilize this crucial mathematical tool in various aspects of your life. The seemingly straightforward calculation of 1% of 12 serves as a gateway to a deeper appreciation of the power and versatility of percentages in our world.
Latest Posts
Latest Posts
-
Spoon Gets Hot In A Bowl Of Soup
Jul 02, 2025
-
How Many Cups In A 16 Oz Sour Cream
Jul 02, 2025
-
How Many 1 4 Teaspoons Are In 1 Teaspoon
Jul 02, 2025
-
How Many Tbsp In A Dry Ounce
Jul 02, 2025
-
How Do You Say Grandparents In Spanish
Jul 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 Percent Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.