What Is 1 To The Power Of 2
Kalali
Apr 12, 2025 · 5 min read
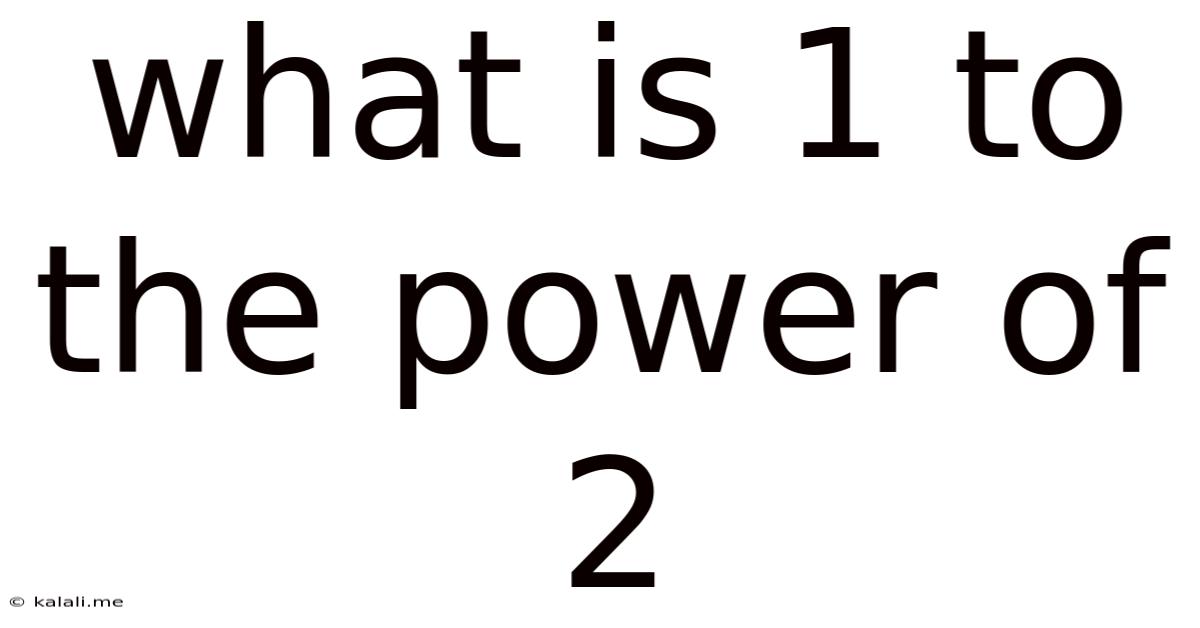
Table of Contents
What is 1 to the Power of 2? A Deep Dive into Exponents and Their Applications
This seemingly simple question, "What is 1 to the power of 2?", opens the door to a fascinating exploration of exponents, their properties, and their wide-ranging applications in mathematics, science, and even everyday life. While the answer itself is straightforward (1² = 1), understanding the underlying concepts provides a solid foundation for tackling more complex mathematical problems. This article will delve into the core principles of exponentiation, explore the specific case of 1 raised to any power, and demonstrate its relevance in various fields.
Meta Description: Learn the answer to "What is 1 to the power of 2?" and explore the broader world of exponents. This article delves into the fundamentals of exponentiation, explains why 1 raised to any power equals 1, and showcases its applications in various fields.
Understanding Exponents: A Foundation
Before tackling 1 to the power of 2, let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. For example, in the expression 2³, the base is 2, and the exponent is 3. This means 2 multiplied by itself three times: 2 × 2 × 2 = 8.
We can represent this mathematically as:
- bⁿ = b × b × b × ... × b (n times)
where 'b' is the base and 'n' is the exponent.
The Special Case of 1 as a Base
Now, let's focus on the case where the base is 1. Regardless of the exponent, 1 raised to any power always equals 1. This is because multiplying 1 by itself any number of times will always result in 1.
Let's look at a few examples:
- 1¹ = 1 (One multiplied by itself once is one)
- 1² = 1 (One multiplied by itself twice is one)
- 1³ = 1 (One multiplied by itself three times is one)
- 1ⁿ = 1 (One multiplied by itself 'n' times is one)
This seemingly trivial result holds significant implications and is a crucial property used in many mathematical and scientific calculations.
Mathematical Proof and Properties of Exponents
The consistent result of 1 raised to any power can be proven mathematically using the properties of exponents. One such property is the identity property of multiplication, which states that any number multiplied by 1 remains unchanged. Since exponentiation is repeated multiplication, this property directly applies.
Another important property is the zero exponent rule: any non-zero base raised to the power of zero equals 1 (b⁰ = 1, where b ≠ 0). This rule is consistent with the pattern of decreasing exponents:
b³ = b × b × b b² = b × b b¹ = b b⁰ = 1
This progression logically leads to the conclusion that 1 raised to any power, including zero, remains 1.
Applications of Exponents and the Significance of 1ⁿ = 1
Exponents are not just abstract mathematical concepts; they are fundamental tools used across various disciplines. Here are a few examples where the understanding of 1 raised to any power plays a role:
1. Compound Interest Calculations
In finance, compound interest calculations heavily rely on exponents. The formula for compound interest involves raising (1 + interest rate) to the power of the number of compounding periods. Even if the initial principal is 1, the exponent dictates the growth over time. Understanding that 1 raised to any power remains 1 provides a baseline for analyzing growth scenarios.
2. Probability and Statistics
Probability calculations frequently involve exponents. Consider the probability of an event happening repeatedly. If the probability of a single event is 1 (certainty), then the probability of that event happening multiple times is still 1, regardless of the number of times it's repeated. This concept directly relates to 1 raised to any power equaling 1.
3. Computer Science and Binary Systems
In computer science, binary systems represent data using only two digits: 0 and 1. Exponents play a crucial role in representing numbers in binary form. Understanding the properties of 1 in exponential calculations is fundamental to interpreting and manipulating binary data.
4. Scientific Notation and Large Numbers
Scientific notation uses exponents to represent extremely large or small numbers concisely. For instance, Avogadro's number (approximately 6.022 × 10²³), represents a vast quantity using exponents. While not directly involving 1 as a base, understanding the behavior of exponents is crucial for manipulating and interpreting these numbers.
5. Geometric Series and Sequences
Geometric series and sequences utilize exponents to define their terms. Understanding the behavior of 1 in exponential contexts is valuable for analyzing and calculating sums and limits of geometric progressions, which have applications in various areas, including finance and physics.
Beyond the Basics: Complex Numbers and Exponents
The principles discussed so far apply primarily to real numbers. When we extend our exploration to complex numbers, things get more interesting. A complex number has a real and an imaginary part, expressed in the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit (√-1). Raising complex numbers to powers involves different rules and considerations, including Euler's formula, which connects exponential functions to trigonometric functions. While 1 raised to any real power is still 1, the behavior of 1 raised to complex powers introduces further mathematical intricacies.
Conclusion: The Unassuming Power of 1
While the answer to "What is 1 to the power of 2?" is a simple "1," the journey to understanding this seemingly trivial calculation reveals the underlying power and importance of exponents in mathematics and various scientific disciplines. The consistent result of 1 raised to any power, stemming from fundamental mathematical properties, serves as a cornerstone for more advanced calculations and models. From financial applications to probability and computer science, the concept of exponentiation and the unique behavior of 1 as a base underpin a wide range of computations and analyses. This seemingly simple question opens a world of mathematical exploration and practical application, emphasizing the importance of understanding fundamental concepts to tackle more complex challenges. The consistent outcome, 1, provides a crucial baseline for interpreting and applying exponential functions in various fields.
Latest Posts
Latest Posts
-
How Many Inches Is 171 Cm
Apr 18, 2025
-
30 Meters Is How Many Yards
Apr 18, 2025
-
What Is 1 Percent Of A Million
Apr 18, 2025
-
How To Find Area Of A Non Right Triangle
Apr 18, 2025
-
Why Is Atp Necessary For Active Transport
Apr 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.