What Is 10 Percent Of 150
Kalali
Apr 19, 2025 · 6 min read
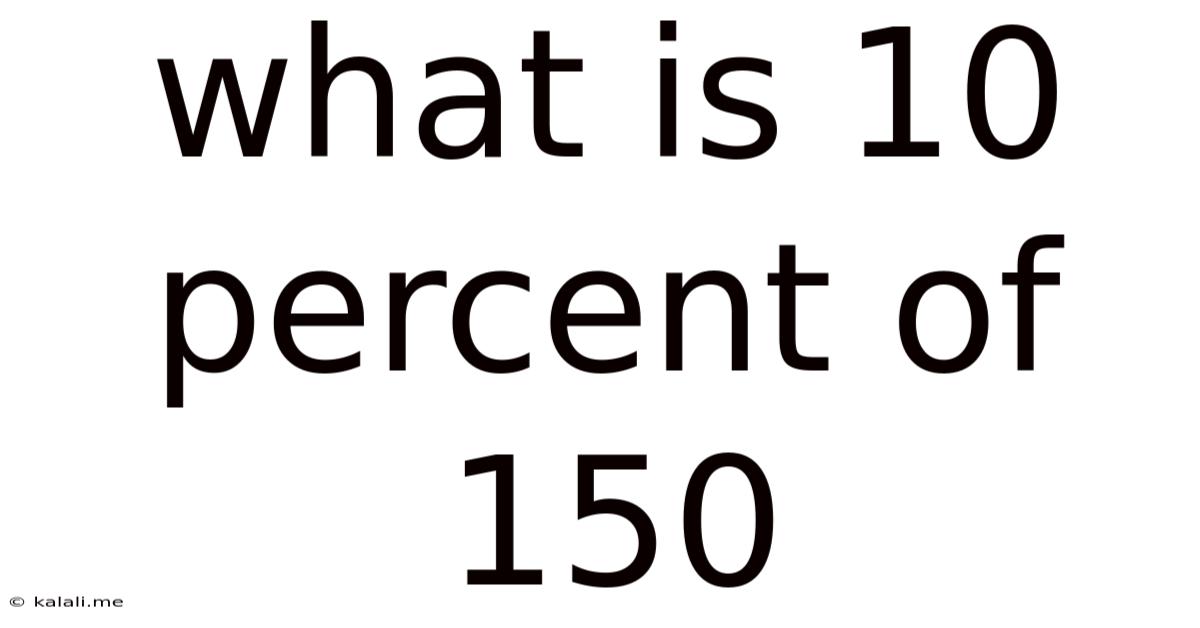
Table of Contents
What is 10 Percent of 150? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 10 percent of 150?", opens the door to a fascinating world of percentages, their practical applications, and the underlying mathematical principles. While the answer itself is easily calculable (15), the journey to understanding how to arrive at that answer, and the broader implications of percentage calculations, offers significant value. This article will explore not only the solution but also delve into the various methods for calculating percentages, their relevance in everyday life, and advanced applications in fields like finance and statistics.
Meta Description: Discover how to calculate 10 percent of 150 and explore the world of percentages, from basic calculations to advanced applications in finance, statistics, and everyday life. Learn multiple methods and understand the practical implications of percentage calculations.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself is derived from the Latin "per centum," meaning "out of a hundred." Therefore, 10 percent means 10 out of 100, or 10/100, which simplifies to 1/10. This fundamental understanding is crucial for tackling any percentage calculation.
To find a percentage of a number, we essentially perform a multiplication. The formula is:
(Percentage/100) * Number = Result
In our case, we want to find 10 percent of 150:
(10/100) * 150 = 15
Therefore, 10 percent of 150 is 15. This simple calculation demonstrates the core principle behind percentage computations.
Different Methods for Calculating Percentages
While the above method is straightforward, several other techniques can be used to calculate percentages, each offering its own advantages depending on the context and individual preference.
Method 1: Using the Formula (as shown above)
This is the most direct and widely applicable method. It's particularly useful for complex percentage calculations or when dealing with decimals.
Method 2: Converting to a Decimal
Percentages can be easily converted into decimals by dividing by 100. In our example, 10 percent becomes 0.10. Multiplying this decimal by the number gives the result:
0.10 * 150 = 15
This method is often quicker for mental calculations, especially with commonly used percentages.
Method 3: Using Fractions
As mentioned earlier, percentages can be represented as fractions. 10 percent is equivalent to 1/10. Therefore, finding 10 percent of 150 is the same as finding 1/10 of 150:
150 / 10 = 15
This method is useful for simple percentages and can enhance understanding of the underlying mathematical relationships.
Method 4: Proportion Method
This method sets up a proportion to solve for the unknown value. We can set up the proportion:
10/100 = x/150
Cross-multiplying gives:
10 * 150 = 100 * x
1500 = 100x
x = 1500/100 = 15
This method is particularly helpful for understanding the relationship between the percentage, the whole, and the part.
Applications of Percentage Calculations in Real Life
Percentage calculations are ubiquitous in everyday life, impacting various aspects of our financial and personal decisions. Here are some key areas:
-
Finance: Percentages are fundamental to understanding interest rates on loans and savings accounts, calculating discounts, determining tax rates, analyzing investment returns, and comprehending inflation rates. Understanding percentages allows for informed financial planning and decision-making. For example, calculating the interest accrued on a savings account or the total cost of an item after sales tax involves direct applications of percentage calculations.
-
Shopping: Sales, discounts, and markdowns are commonly expressed as percentages. Knowing how to quickly calculate these percentages allows for more efficient shopping and helps you identify the best deals. For example, a 20% discount on a $100 item translates to a $20 savings.
-
Statistics and Data Analysis: Percentages are widely used to represent proportions and trends in data. Graphs and charts often display data as percentages, making it easier to visualize and understand complex information. For instance, understanding the percentage of a population that falls into a particular demographic group or the percentage change in a certain metric over time are vital in statistics.
-
Science and Engineering: Percentages are used in various scientific and engineering calculations, from expressing concentrations of solutions to calculating error margins in experiments.
-
Health and Nutrition: Nutrition labels on food products frequently list percentages of daily recommended values for nutrients like vitamins and minerals. Understanding these percentages assists in maintaining a healthy diet.
Advanced Percentage Calculations and Concepts
Beyond the basics, several more advanced percentage calculations and concepts exist:
- Percentage Increase and Decrease: Calculating the percentage increase or decrease between two values is common. The formula for percentage increase is:
[(New Value - Old Value) / Old Value] * 100
Similarly, the percentage decrease is calculated as:
[(Old Value - New Value) / Old Value] * 100
-
Compound Interest: Compound interest involves calculating interest not only on the principal amount but also on the accumulated interest. This leads to exponential growth over time and is crucial in understanding long-term investments.
-
Percentage Points: Percentage points represent the absolute difference between two percentages, unlike the percentage change. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% increase in percentage terms.
-
Weighted Averages: Weighted averages are used when certain values contribute more significantly to the overall average. This concept is important in various fields, including finance and academic grading systems.
-
Percentage of a Percentage: This involves calculating a percentage of another percentage. For instance, finding 20% of 5% of 1000 would require sequential percentage calculations.
Real-World Examples of Percentage Calculations
Let's explore some real-world scenarios illustrating the practical application of percentage calculations:
Scenario 1: Sales Tax
If the sales tax in your area is 6%, and you buy an item costing $50, the sales tax amount would be:
(6/100) * $50 = $3
The total cost of the item would be $50 + $3 = $53.
Scenario 2: Discount Calculation
A store offers a 25% discount on a $200 jacket. The discount amount is:
(25/100) * $200 = $50
The final price after the discount is $200 - $50 = $150.
Scenario 3: Investment Return
If you invest $1000 and earn a 10% return, your profit would be:
(10/100) * $1000 = $100
Your total investment value would be $1000 + $100 = $1100.
Scenario 4: Grade Calculation
If you score 80 out of 100 on a test, your percentage score would be:
(80/100) * 100 = 80%
Conclusion
The question, "What is 10 percent of 150?" serves as a springboard to understanding the broader world of percentage calculations. From basic arithmetic to advanced financial and statistical applications, percentages are an integral part of our daily lives. Mastering percentage calculations empowers informed decision-making in various aspects of life, from personal finance to professional pursuits. The diverse methods available for calculating percentages, coupled with a thorough understanding of the underlying principles, allows for efficient and accurate computations, regardless of complexity. Remember that consistent practice and application are key to solidifying your understanding and proficiency in this crucial mathematical skill.
Latest Posts
Latest Posts
-
What Is 30 100 As A Percent
Apr 22, 2025
-
How To Find The Range In A Dot Plot
Apr 22, 2025
-
As Altitude Increases What Happens To Air Pressure
Apr 22, 2025
-
How Big Is 36 Inches In Cm
Apr 22, 2025
-
What Is 0 125 In A Fraction
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Percent Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.