What Is 10 Percent Of 300
Kalali
Mar 26, 2025 · 4 min read
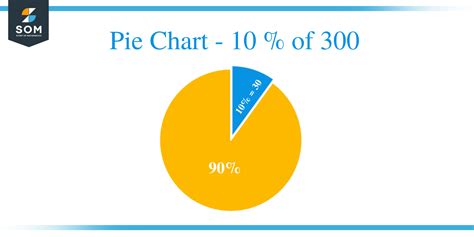
Table of Contents
What is 10 Percent of 300? A Deep Dive into Percentages and Their Applications
Finding 10 percent of 300 might seem like a simple calculation, a piece of cake even. But understanding the underlying principles of percentages and their broad applications extends far beyond this basic arithmetic. This article delves deep into the concept, exploring various methods to calculate percentages, practical examples of their use, and even touches on more advanced percentage-related problems.
Understanding Percentages:
A percentage is simply a fraction expressed as a part of 100. The term "percent" itself derives from the Latin "per centum," meaning "out of one hundred." Therefore, 10 percent means 10 out of 100, or 10/100, which simplifies to 1/10. This fundamental understanding is key to solving any percentage problem.
Method 1: The Simple Multiplication Method (For 10% of 300)
The most straightforward way to calculate 10 percent of 300 is through multiplication. Since 10 percent is equivalent to 0.1 (10 divided by 100), we simply multiply 300 by 0.1:
300 * 0.1 = 30
Therefore, 10 percent of 300 is 30. This method is ideal for quick calculations, particularly when dealing with percentages that are easy to convert into decimals (like 10%, 25%, 50%, etc.).
Method 2: The Fraction Method
As mentioned earlier, 10 percent can also be represented as the fraction 1/10. To find 10 percent of 300 using this method, we multiply 300 by 1/10:
300 * (1/10) = 300/10 = 30
This method reinforces the fractional representation of percentages and is helpful in understanding the underlying mathematical concept. It’s particularly useful when dealing with more complex fractions that aren't easily convertible into decimals.
Method 3: The Proportion Method
The proportion method is a powerful technique applicable to a broader range of percentage problems. It involves setting up a proportion:
Part/Whole = Percentage/100
In our case:
x/300 = 10/100
To solve for x (10% of 300), we cross-multiply:
100x = 3000
x = 3000/100
x = 30
This method demonstrates the relationship between the part, the whole, and the percentage, providing a structured approach to solving percentage problems. It is highly beneficial when dealing with unknowns in either the part, the whole, or the percentage itself.
Real-World Applications of Percentages:
Percentages are ubiquitous in everyday life, finding their way into various fields:
-
Finance: Calculating interest on loans, savings accounts, and investments heavily relies on percentages. Understanding compound interest, for example, requires a solid grasp of percentage calculations. Analyzing financial statements and interpreting key financial ratios also involve percentages.
-
Sales and Discounts: Stores frequently offer discounts expressed as percentages (e.g., 20% off). Calculating the final price after a discount requires percentage calculations. Sales tax is also calculated as a percentage of the purchase price.
-
Statistics and Data Analysis: Percentages are essential for representing data in a concise and easily understandable manner. For example, expressing survey results, demographic breakdowns, or changes in economic indicators often uses percentages. Understanding statistical significance also involves percentage-based calculations.
-
Science and Engineering: Percentages play a critical role in scientific calculations and engineering designs. For instance, calculating the efficiency of a machine, the concentration of a solution, or the error rate in a measurement might utilize percentage calculations.
-
Healthcare: Healthcare professionals frequently use percentages to represent dosage calculations, body fat percentages, or the success rate of medical treatments.
More Complex Percentage Problems:
Let’s explore some more challenging percentage scenarios to build upon our understanding:
1. Finding the Percentage: What percentage of 250 is 50?
We can again utilize the proportion method:
x/100 = 50/250
Cross-multiplying gives:
250x = 5000
x = 20
Therefore, 50 is 20% of 250.
2. Finding the Whole: 30 is 15% of what number?
Using the proportion method:
30/x = 15/100
Cross-multiplying:
15x = 3000
x = 200
Thus, 30 is 15% of 200.
3. Percentage Increase/Decrease: A product's price increased from $100 to $120. What is the percentage increase?
First, find the difference: $120 - $100 = $20
Then, calculate the percentage increase relative to the original price:
($20/$100) * 100% = 20%
The price increased by 20%.
4. Consecutive Percentage Changes: A product is discounted by 20% and then by an additional 10%. What is the total discount?
It's crucial to remember that consecutive percentage changes don't simply add up. Let's assume the original price is $100:
- First discount: $100 * 0.20 = $20 (Price becomes $80)
- Second discount: $80 * 0.10 = $8 (Price becomes $72)
The total discount is $100 - $72 = $28, which is 28% of the original price. Notice that it’s not simply 20% + 10% = 30%.
Conclusion:
While finding 10 percent of 300 might appear trivial, the broader concept of percentages and their diverse applications are profoundly significant. Mastering percentage calculations is essential for navigating various aspects of everyday life, from personal finance to professional fields. By understanding the different methods, from simple multiplication to the powerful proportion method, and by practicing with increasingly complex problems, you can confidently tackle any percentage-related challenge. Remember that understanding the underlying principles allows you to adapt these techniques to a multitude of real-world situations, solidifying your grasp of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
What Is The Continuous Flow Of Electric Charge
Mar 29, 2025
-
20 Is What Percent Of 200
Mar 29, 2025
-
9 Out Of 25 As A Percentage
Mar 29, 2025
-
What Is 10 Percent Of 140
Mar 29, 2025
-
Words With In As A Prefix
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Percent Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
