What Is 10 Percent Of 40
Kalali
Mar 29, 2025 · 5 min read
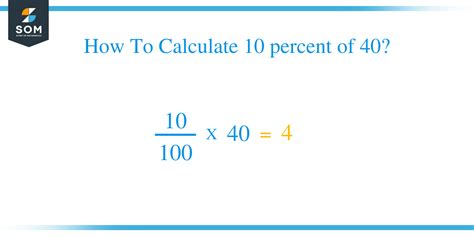
Table of Contents
What is 10 Percent of 40? A Deep Dive into Percentages and Their Applications
The seemingly simple question, "What is 10 percent of 40?" opens the door to a broader understanding of percentages, their practical applications, and their importance in various fields. While the answer itself is straightforward (4), the journey to understanding how to calculate percentages and their significance is far more enriching. This article will not only answer the question but delve into the underlying concepts, explore diverse applications, and provide you with the tools to tackle similar percentage problems with confidence.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." This fundamental concept is crucial in understanding how percentages work. When we say 10 percent, we are essentially saying 10 out of 100, which can be represented as a fraction (10/100) or a decimal (0.10).
Calculating 10 Percent of 40: The Simple Approach
To calculate 10 percent of 40, we can use a simple formula:
(Percentage/100) * Total Value = Result
Substituting the values, we get:
(10/100) * 40 = 4
Therefore, 10 percent of 40 is 4. This calculation can be simplified further by recognizing that 10/100 simplifies to 1/10. So, finding 10% of a number is the same as dividing that number by 10.
Beyond the Basics: Different Methods for Calculating Percentages
While the above method is straightforward, there are several other approaches to calculating percentages, each offering unique advantages depending on the situation:
-
Using Decimal Equivalents: Converting the percentage to its decimal equivalent simplifies the calculation. 10% is equivalent to 0.10. Multiplying 40 by 0.10 gives you 4. This method is particularly efficient for mental calculations.
-
Using Proportions: Setting up a proportion can be helpful, especially for more complex percentage problems. For example:
x/40 = 10/100
Solving for x will give you the answer. Cross-multiplying gives 100*x = 400, and solving for x yields 4.
-
Using a Calculator: For larger numbers or more complex percentage calculations, a calculator is invaluable. Most calculators have a percentage function (%) that streamlines the process.
Real-World Applications of Percentages: Where They Matter
Percentages are not just abstract mathematical concepts; they are deeply embedded in our daily lives, playing a crucial role in various fields:
-
Finance: Percentages are fundamental in finance. Interest rates on loans, savings accounts, and investments are all expressed as percentages. Calculating discounts, taxes, tips, and profits all rely heavily on percentage calculations. Understanding compound interest, for instance, requires a strong grasp of percentages.
-
Statistics: In statistics, percentages are used to represent data proportions, allowing for easier interpretation and comparison. For example, survey results, election polls, and demographic data are often presented using percentages. Understanding statistical significance and confidence intervals also involves working with percentages.
-
Science: Percentages are used extensively in science to express concentrations, yields, and error margins. For example, the percentage composition of elements in a chemical compound, the percentage yield of a chemical reaction, or the percentage error in an experiment are all expressed as percentages.
-
Retail and Sales: Businesses use percentages for pricing strategies, offering discounts, and calculating profit margins. Sales tax, markups, and markdown percentages are essential tools for businesses to manage pricing and profitability. Understanding these percentages is crucial for both consumers and businesses.
-
Healthcare: Percentages are critical in healthcare for dosage calculations, interpreting lab results, and tracking disease prevalence. For example, a doctor might prescribe a medication dosage as a percentage of a patient's body weight. Similarly, lab results may be reported as a percentage of a normal range.
Beyond 10 Percent of 40: Tackling More Complex Percentage Problems
Understanding the fundamental concepts allows you to tackle more complex percentage problems. Let's explore some examples:
Example 1: Finding the Percentage:
What percentage of 80 is 20?
To solve this, we use the formula:
(Part/Whole) * 100 = Percentage
(20/80) * 100 = 25%
Therefore, 20 is 25% of 80.
Example 2: Finding the Whole:
20% of a number is 10. What is the number?
Let's represent the unknown number as x. We set up the equation:
0.20 * x = 10
Solving for x, we get:
x = 10 / 0.20 = 50
Therefore, the number is 50.
Example 3: Percentage Increase/Decrease:
A product's price increased from $40 to $50. What is the percentage increase?
First, find the difference: $50 - $40 = $10
Then, divide the difference by the original price: $10 / $40 = 0.25
Finally, multiply by 100 to get the percentage: 0.25 * 100 = 25%
The price increased by 25%.
Mastering Percentages: Tips and Tricks
-
Practice Regularly: The more you practice, the better you'll become at solving percentage problems. Work through various examples and challenge yourself with different scenarios.
-
Use Visual Aids: Visual aids like charts and diagrams can help you understand percentages more intuitively.
-
Understand the Context: Pay close attention to the wording of the problem to ensure you're using the correct formula and approach.
-
Break Down Complex Problems: Complex percentage problems can be broken down into smaller, more manageable steps.
-
Check Your Answers: Always check your answers to ensure they are logical and consistent with the problem's context.
Conclusion: The Power of Percentages
The seemingly simple calculation of 10 percent of 40 reveals the broader importance and extensive applications of percentages in our lives. From finance and statistics to science and retail, understanding percentages is a crucial skill that enhances problem-solving abilities and provides valuable insights into various fields. By mastering the concepts and techniques discussed in this article, you'll be equipped to confidently tackle percentage problems and leverage this powerful tool in your personal and professional life. Remember, consistent practice and a thorough understanding of the underlying principles are key to achieving mastery.
Latest Posts
Latest Posts
-
How Tall Is 82 Inches In Feet
Mar 31, 2025
-
How Long Should It Take To Boil Water
Mar 31, 2025
-
How Many Inches Is 4 Ft 9
Mar 31, 2025
-
Words That End In C K
Mar 31, 2025
-
101 Do F Bang Bao Nhieu Do C
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
