What Is 10 Times 10 Times 10
Kalali
Jul 19, 2025 · 5 min read
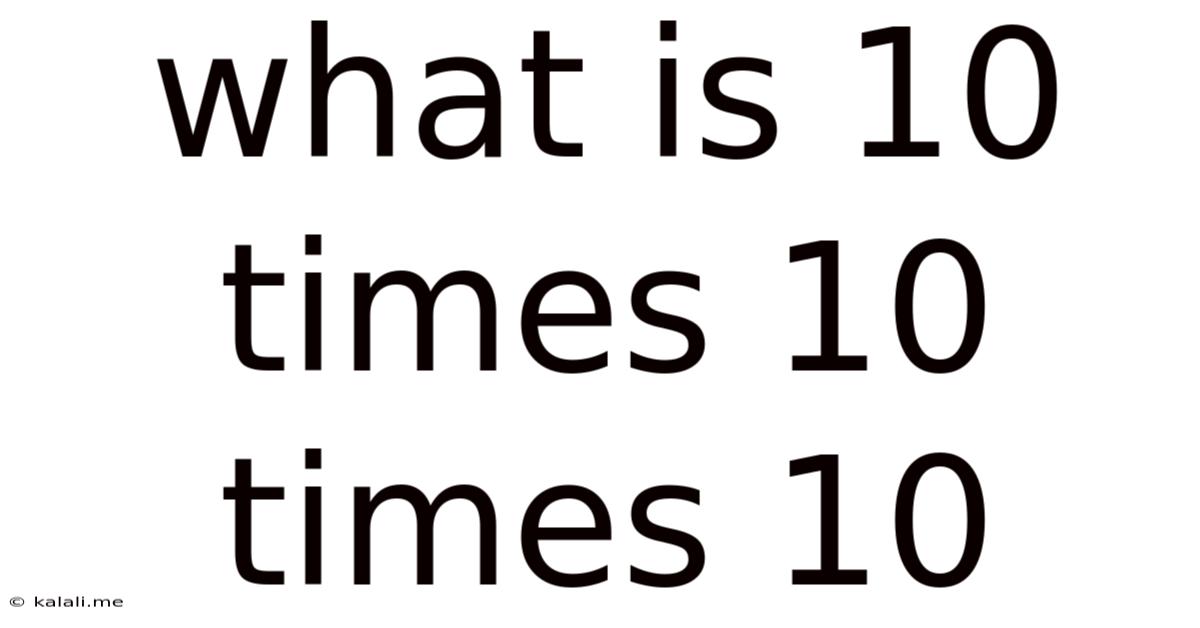
Table of Contents
What is 10 Times 10 Times 10? Unpacking Multiplication and its Applications
What is 10 times 10 times 10? The answer, of course, is 1000. But this seemingly simple mathematical problem opens a door to a much wider exploration of multiplication, its practical applications, and the underlying concepts that govern it. This article delves into the intricacies of this calculation, exploring its significance in various fields and providing a comprehensive understanding of its implications.
Understanding the Fundamentals of Multiplication
At its core, multiplication is a shortcut for repeated addition. When we say "10 times 10 times 10," we're essentially asking: what is the result of adding ten to itself ten times, and then taking that result and adding it to itself ten more times? While this repeated addition approach is conceptually straightforward, it becomes cumbersome for larger numbers. Multiplication provides an efficient method to streamline this process.
The expression "10 times 10 times 10" can be written mathematically as 10 x 10 x 10, or more concisely as 10³. This notation introduces the concept of exponents, where the base number (10) is multiplied by itself the number of times indicated by the exponent (3). This exponential notation is crucial for representing and working with larger numbers efficiently.
Calculating 10 x 10 x 10
The calculation itself is relatively straightforward. First, we multiply 10 by 10, which equals 100. Then, we multiply this result by 10 again, yielding 1000. This simple sequence highlights the power of exponential growth, where each successive multiplication leads to a significantly larger outcome. Understanding this growth is fundamental in various fields, from finance to computer science.
Practical Applications of Multiplication and Exponential Growth
The concept of multiplying a number by itself multiple times (exponentiation) has far-reaching implications across numerous disciplines:
-
Finance: Compound interest, a cornerstone of financial planning, relies heavily on exponential growth. If you invest a principal amount and earn a certain percentage interest each year, the interest earned in subsequent years is calculated not only on the principal but also on the accumulated interest from previous years. This snowball effect is a direct consequence of repeated multiplication. Calculating future value of investments, understanding loan amortization schedules, and even projecting the growth of savings all depend on the ability to work with exponential functions.
-
Computer Science: Binary numbers, the foundation of digital computing, use the base-2 number system. Data is represented using combinations of 0s and 1s, and the power of 2 (2¹, 2², 2³, etc.) plays a vital role in calculating data storage capacity, processing power, and network speeds. For example, understanding that 1024 (2¹⁰) bytes equal 1 kilobyte is crucial in comprehending data sizes and memory management.
-
Physics and Engineering: Exponential functions are prevalent in physical phenomena. Radioactive decay, population growth (under ideal conditions), and the spread of diseases can often be modeled using exponential equations. Understanding these models is critical for predicting future trends and making informed decisions in various fields. Understanding exponential growth is essential in predicting the trajectory of rockets and the effects of atmospheric pressure.
-
Geometry and Measurement: Calculating the volume of a cube involves multiplying the length, width, and height. If all sides are equal, as in a cube with sides of 10 units, then the volume is 10 x 10 x 10 = 1000 cubic units. This simple application of multiplication extends to calculating the volume of more complex shapes and objects.
-
Data Analysis and Statistics: Exponential distributions are common in statistics. They're used to model various phenomena, such as the time between events in a Poisson process or the distribution of certain types of data. Understanding these distributions is vital for statistical analysis and decision-making.
Expanding the Concept: Beyond 10 x 10 x 10
While the initial question focused on 10 x 10 x 10, the underlying principles apply to any base number and exponent. Consider the following examples:
-
2 x 2 x 2 = 8 (2³): This illustrates exponential growth with a smaller base number. The result is still significantly larger than the initial number.
-
5 x 5 x 5 = 125 (5³): This demonstrates that the magnitude of the result increases as the base number increases.
-
100 x 100 x 100 = 1,000,000 (100³): This highlights the rapid growth of exponential functions, especially with larger base numbers.
Understanding these variations is crucial for grasping the breadth of applications of exponential functions.
Scientific Notation and Large Numbers
As we deal with increasingly large numbers, scientific notation becomes indispensable. Scientific notation expresses numbers in the form a x 10^b, where 'a' is a number between 1 and 10, and 'b' is the exponent representing the power of 10. For instance, 1000 can be written as 1 x 10³. This notation simplifies the representation and manipulation of very large or very small numbers, which are commonly encountered in scientific and engineering applications. Mastering scientific notation is essential for effectively communicating and working with data in these fields.
The Importance of Understanding Multiplication in Everyday Life
While the complexities of exponential growth and scientific notation might seem abstract, the underlying principle of multiplication is deeply ingrained in our daily lives. From calculating the total cost of groceries to determining the amount of paint needed for a project, multiplication is an essential skill for practical problem-solving. It’s the foundation for understanding proportions, ratios, and many other mathematical concepts that are crucial for navigating the complexities of modern life.
Conclusion: A Foundation for Further Learning
The seemingly simple question, "What is 10 times 10 times 10?" serves as a springboard to explore the fascinating world of mathematics, specifically multiplication and exponential functions. The answer, 1000, is not just a numerical result but a representation of the power of repeated multiplication and its extensive applications across various disciplines. Understanding these principles is crucial for comprehending complex systems, making informed decisions, and fostering a deeper appreciation for the role of mathematics in our world. From finance and technology to scientific research and everyday life, the concept of multiplication is a cornerstone of knowledge and problem-solving, offering a pathway for continued learning and exploration. The journey begins with a simple calculation, but the implications extend far beyond.
Latest Posts
Latest Posts
-
Are Janet Davies And Mark Giangreco Married
Jul 19, 2025
-
Born In 86 How Old Am I
Jul 19, 2025
-
How Much Is 115 Grams Of Butter
Jul 19, 2025
-
How Much Is 400 Grams In Oz
Jul 19, 2025
-
The Value Does Not Match The Pattern Aa
Jul 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Times 10 Times 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.