What Is 10 To The -3 Power
Kalali
Apr 12, 2025 · 5 min read
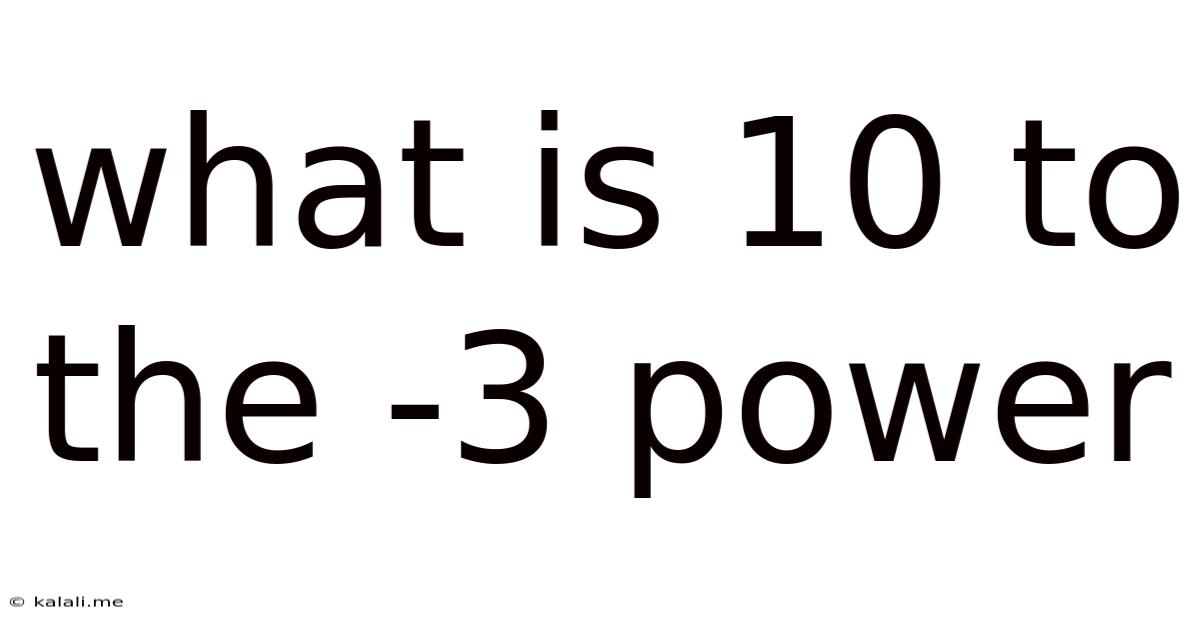
Table of Contents
What is 10 to the -3 Power? A Deep Dive into Negative Exponents and Scientific Notation
What does 10 to the -3 power mean? This seemingly simple question opens a door to a fundamental concept in mathematics and science: negative exponents and their crucial role in scientific notation. Understanding this concept is key to comprehending various scientific measurements, calculations, and data representations. This article will thoroughly explore the meaning of 10⁻³, its applications, and its broader implications within the realm of exponential notation.
Meta Description: Unlock the mystery of 10 to the -3 power! This comprehensive guide explains negative exponents, scientific notation, real-world applications, and how to easily perform calculations involving negative powers of 10. Learn about its significance in science, engineering, and everyday life.
Understanding Exponents and their Significance
Before delving into the specifics of 10⁻³, let's establish a foundational understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example, in the expression 10³, the base is 10 and the exponent is 3. This means 10 multiplied by itself three times: 10 x 10 x 10 = 1000.
Exponents provide a concise way to represent very large or very small numbers. This efficiency is particularly valuable in scientific fields where dealing with extremely large or small quantities is commonplace. For instance, the distance to the sun or the size of an atom are more easily expressed using exponents.
Deciphering Negative Exponents: The Reciprocal Rule
Negative exponents introduce a crucial twist to the concept. A negative exponent signifies the reciprocal of the base raised to the positive power of that exponent. In simpler terms, it means "one over" the base number raised to the positive exponent.
Therefore, 10⁻³ is the same as 1/(10³). Since 10³ = 1000, 10⁻³ = 1/1000 = 0.001.
This reciprocal rule is a cornerstone of understanding negative exponents. It allows us to translate a seemingly complex expression into a more manageable and understandable decimal value.
10 to the -3 Power in Scientific Notation
Scientific notation is a standardized way of expressing numbers, particularly very large or very small ones. It uses a base of 10 raised to a power (exponent) to represent the number. The general form is:
m x 10ⁿ
where 'm' is a number between 1 and 10 (but not including 10) and 'n' is the exponent, which can be positive or negative.
Using this notation, 0.001 would be written as 1 x 10⁻³. Here, 'm' is 1 and 'n' is -3. This demonstrates how 10⁻³ becomes a fundamental building block for representing small numbers using scientific notation.
Real-World Applications of 10⁻³
The significance of 10⁻³ extends beyond theoretical mathematics. It finds practical applications in various fields:
-
Metric System: The metric system heavily relies on powers of 10. Milli (m) is a prefix denoting 10⁻³, meaning one-thousandth. Thus, 1 millimeter (mm) is equal to 0.001 meters (m). This is widely used in measurements of length, volume, and mass. Understanding 10⁻³ is essential for conversions within the metric system. For example, converting cubic millimeters to cubic meters involves using 10⁻⁹ (10⁻³ cubed).
-
Chemistry and Physics: In chemistry, concentrations of solutions are often expressed in molarity (moles per liter). A 10⁻³ molar solution, often written as 1 mM (millimolar), indicates a solution with a concentration of 0.001 moles of solute per liter of solvent. Similar applications are seen in expressing various physical quantities like charge, energy, and pressure.
-
Computer Science: While not directly using the notation 10⁻³, the underlying principle of negative exponents plays a role in representing data storage. A kilobyte, for example, is 1024 bytes, a power of two, but the approximate relationship to 1000 (10³) is frequently used for estimation. Its inverse, in a sense, reflects the application of negative exponents.
-
Engineering: In engineering design and calculations, 10⁻³ appears in various contexts. For instance, tolerance levels for dimensions might be expressed as 10⁻³ of a meter, representing very small allowable deviations.
Calculations with 10 to the -3 Power
Performing calculations involving 10⁻³ is straightforward, especially when utilizing scientific notation. Here are some examples:
-
Multiplication: Multiplying a number by 10⁻³ is equivalent to dividing it by 1000. For example, 5 x 10⁻³ = 0.005. Similarly, 2500 x 10⁻³ = 2.5.
-
Division: Dividing a number by 10⁻³ is equivalent to multiplying it by 1000. For example, 0.005 / 10⁻³ = 5.
-
Exponentiation: Raising 10⁻³ to another power, like (10⁻³)² is found by multiplying the exponents: 10⁻⁶ = 0.000001.
-
Working with other powers of 10: When dealing with other powers of 10, remember the rules of exponent manipulation. For example, 10⁻³ x 10² = 10⁻¹ = 0.1.
These examples illustrate how using the basic rules of exponents, particularly with respect to negative exponents, significantly simplifies calculations involving 10⁻³.
Distinguishing 10⁻³ from other Small Numbers
It's crucial to differentiate 10⁻³ from other small numbers expressed using different exponents or notations. For instance:
-
10⁻² (0.01): This is ten times larger than 10⁻³.
-
10⁻⁴ (0.0001): This is one-tenth of 10⁻³.
-
0.0005: This is half of 10⁻³, illustrating how 10⁻³ serves as a useful reference point for understanding the magnitude of small numbers.
Understanding these distinctions is key to avoiding errors in calculations and interpretations.
Beyond 10⁻³: Exploring the Broader Spectrum of Negative Exponents
The concept of 10⁻³ is just one point within the larger context of negative exponents. Understanding this concept extends to other bases and exponents. For example:
-
2⁻³: This would be 1/(2³) = 1/8 = 0.125.
-
5⁻²: This would be 1/(5²) = 1/25 = 0.04.
The fundamental principles remain the same: a negative exponent indicates the reciprocal of the base raised to the positive exponent.
Conclusion: The Practical Utility of 10⁻³ and its Implications
In conclusion, 10 to the -3 power, representing 0.001 or 1 x 10⁻³, is more than just a mathematical abstraction. It's a fundamental concept with far-reaching implications in various scientific and practical applications. Understanding this concept, its role in scientific notation, and its manipulation in calculations empowers us to handle vast quantities and tiny measurements with precision and ease. From understanding the metric system to interpreting scientific data, mastering the principles of negative exponents is key to unlocking a deeper understanding of the world around us. By grasping this core concept, we become better equipped to navigate the complexities of numbers and apply this knowledge across numerous disciplines.
Latest Posts
Latest Posts
-
What Is Double Of 1 4 Cup
Jul 10, 2025
-
Prepare Me A Body And I Will Redeem Man
Jul 10, 2025
-
How Many Inches Is A Meter Stick
Jul 10, 2025
-
Soundtrack To Step Up 2 The Streets
Jul 10, 2025
-
Keebler Club And Cheddar Crackers Expiration Date
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 To The -3 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.