What Is 12/15 As A Percentage
Kalali
Apr 14, 2025 · 5 min read
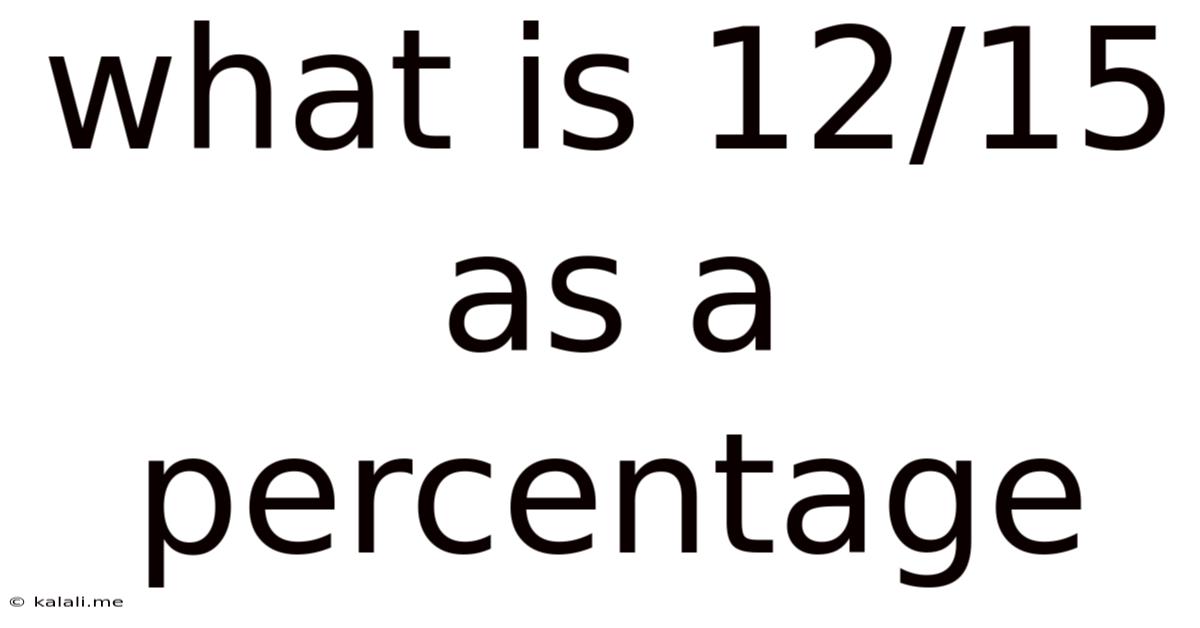
Table of Contents
What is 12/15 as a Percentage? A Comprehensive Guide to Fraction-to-Percentage Conversions
Knowing how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding statistical data and financial reports. This article delves into the process of converting the fraction 12/15 into a percentage, explaining the underlying principles and providing various methods to achieve this conversion. We'll also explore related concepts and offer practical examples to solidify your understanding. This comprehensive guide will equip you with the tools to confidently tackle similar fraction-to-percentage conversions.
Meta Description: Learn how to convert the fraction 12/15 into a percentage. This guide provides multiple methods, explains the underlying principles, and offers practical examples for a complete understanding of fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before we dive into the conversion, let's establish a clear understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or 1/2.
The key to converting a fraction to a percentage is to express the fraction as an equivalent fraction with a denominator of 100. This allows us to directly read the percentage from the numerator.
Method 1: Simplifying the Fraction and then Converting
The fraction 12/15 can be simplified before converting it to a percentage. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 12 and 15 is 3.
Therefore, we divide both the numerator and the denominator by 3:
12 ÷ 3 = 4 15 ÷ 3 = 5
This simplifies the fraction 12/15 to 4/5.
Now, to convert 4/5 to a percentage, we need to find an equivalent fraction with a denominator of 100. We can do this by multiplying both the numerator and the denominator by 20 (since 5 x 20 = 100):
4 x 20 = 80 5 x 20 = 100
So, 4/5 is equal to 80/100. Therefore, 12/15 as a percentage is 80%.
Method 2: Converting the Fraction to a Decimal and then to a Percentage
Another common method is to first convert the fraction to a decimal and then multiply by 100 to express it as a percentage. To convert 12/15 to a decimal, we divide the numerator by the denominator:
12 ÷ 15 = 0.8
Now, to convert the decimal 0.8 to a percentage, we multiply it by 100:
0.8 x 100 = 80
Therefore, 12/15 as a percentage is 80%. This method is particularly useful when dealing with fractions that are not easily simplified to have a denominator of 100.
Method 3: Using Proportions to Solve
We can also use proportions to solve this problem. We can set up a proportion:
12/15 = x/100
Where 'x' represents the percentage we are trying to find. To solve for x, we cross-multiply:
12 * 100 = 15 * x 1200 = 15x
Now, divide both sides by 15:
x = 1200 ÷ 15 x = 80
Therefore, 12/15 as a percentage is 80%.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages has numerous practical applications across various fields:
-
Finance: Calculating interest rates, discounts, tax rates, and profit margins often involves converting fractions to percentages. For example, if a store offers a 1/4 discount, you would convert this to 25% to calculate the final price.
-
Statistics: Representing data in percentages is crucial for understanding and interpreting statistical information. For example, if 3 out of 5 people prefer a particular product (3/5), converting this to 60% makes the data more accessible and easier to compare.
-
Science: Many scientific calculations involve expressing results as percentages, such as the percentage composition of a chemical compound or the percentage yield of a chemical reaction.
-
Everyday Life: Calculating tips in restaurants, understanding sale prices, and determining the percentage of completion of a project all rely on the ability to convert fractions to percentages.
Further Exploration: Working with More Complex Fractions
While 12/15 is a relatively straightforward fraction, the principles discussed here apply to more complex fractions as well. For instance, consider a fraction like 27/45. You could follow the same steps:
- Simplify the fraction: The GCD of 27 and 45 is 9. Simplifying gives you 3/5.
- Convert to a percentage: Multiplying both numerator and denominator by 20 gives you 60/100, or 60%.
- Alternatively, convert to a decimal first: 27 ÷ 45 = 0.6. Multiplying by 100 gives you 60%.
- Or use proportions: 27/45 = x/100 => x = 60.
Remember, the core concept remains the same: Express the fraction as an equivalent fraction with a denominator of 100 or convert it to a decimal and then multiply by 100.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a crucial skill that transcends academic settings and finds widespread application in everyday life. By understanding the underlying principles and employing the different methods outlined in this guide, you can confidently tackle a wide range of fraction-to-percentage conversion problems. Practice is key to mastering this skill, so don't hesitate to work through various examples to solidify your understanding. The ability to quickly and accurately convert fractions to percentages will undoubtedly enhance your mathematical proficiency and broaden your problem-solving capabilities. Remember that the key is to find the method that works best for you and consistently apply the principles to achieve accurate results.
Latest Posts
Latest Posts
-
How Much Older Is John The Baptist Than Jesus
Jul 12, 2025
-
How Many Teaspoons In A Pound Of Sugar
Jul 12, 2025
-
How Do You Pass Level 12 On Bloxorz
Jul 12, 2025
-
How Far Is 0 4 Miles To Walk
Jul 12, 2025
-
What Is 20 Percent Of 800 000
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 12/15 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.