What Is 12/25 As A Percentage
Kalali
Apr 09, 2025 · 5 min read
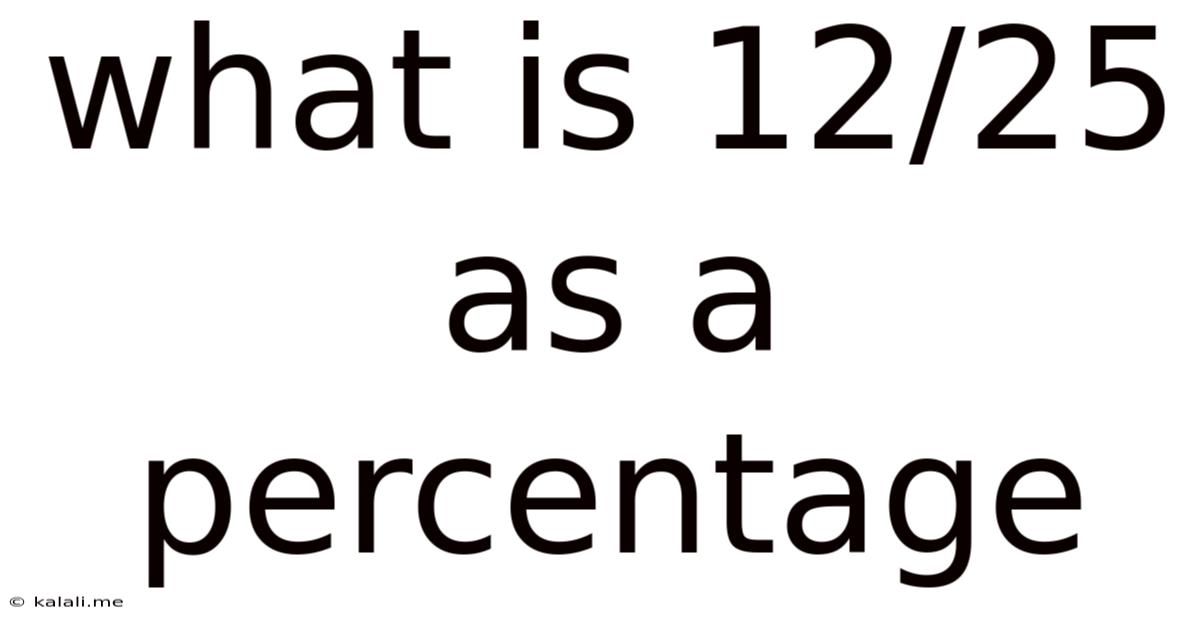
Table of Contents
What is 12/25 as a Percentage? A Comprehensive Guide to Fraction-to-Percentage Conversions
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday calculations. This article delves deep into the conversion of the fraction 12/25 to a percentage, exploring multiple methods and offering a broader understanding of fraction-to-percentage conversions. We'll not only show you how to do it but also why it works, equipping you with the knowledge to tackle similar conversions with confidence.
Meta Description: Learn how to convert the fraction 12/25 into a percentage using several methods. This comprehensive guide explains the process step-by-step, providing a thorough understanding of fraction-to-percentage conversions and their applications.
Understanding Fractions and Percentages
Before we jump into the conversion, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 12/25, 12 is the numerator and 25 is the denominator. This means we have 12 parts out of a total of 25 parts.
A percentage, on the other hand, represents a fraction out of 100. The symbol "%" denotes percentage. So, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. Percentages provide a standardized way to compare fractions and proportions, making them easier to understand and interpret.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This is arguably the most common and straightforward method. It involves two steps:
-
Convert the fraction to a decimal: To do this, we simply divide the numerator (12) by the denominator (25).
12 ÷ 25 = 0.48
-
Convert the decimal to a percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.48 × 100 = 48%
Therefore, 12/25 as a percentage is 48%.
This method is particularly useful when dealing with fractions that don't easily simplify to a fraction with a denominator of 100.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. This is a direct approach because percentages are essentially fractions with a denominator of 100.
To find an equivalent fraction, we need to determine what number we can multiply the denominator (25) by to get 100. In this case, 25 multiplied by 4 equals 100. Crucially, we must perform the same operation on both the numerator and denominator to maintain the fraction's value:
(12 × 4) / (25 × 4) = 48/100
Since 48/100 means 48 out of 100, it directly translates to 48%.
This method is efficient when the denominator is a simple factor of 100 (like 25, 50, or 20). It offers a clear visual representation of the percentage.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. We can set up a proportion:
12/25 = x/100
Here, 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
12 × 100 = 25 × x
1200 = 25x
x = 1200 ÷ 25
x = 48
Therefore, 12/25 is equal to 48%.
This method is particularly useful when dealing with more complex fractions or when you need a more formal mathematical approach to the problem.
Understanding the Context: Applications of Percentage Conversions
The ability to convert fractions to percentages is crucial in various real-world scenarios. Consider these examples:
- Finance: Calculating interest rates, discounts, and profit margins often involve converting fractions to percentages. For instance, if a store offers a 12/25 discount on an item, knowing that this translates to a 48% discount helps customers understand the savings more easily.
- Statistics: Data analysis and interpretation often rely on representing data as percentages. For example, if 12 out of 25 people surveyed prefer a particular product, expressing this as 48% provides a concise and easily understandable summary of the data.
- Everyday Life: Calculating tips, splitting bills, or understanding sales often requires converting fractions to percentages for easier comprehension.
Advanced Concepts and Further Exploration
While the conversion of 12/25 to 48% is relatively straightforward, understanding the underlying principles allows you to tackle more complex scenarios. These include:
- Converting mixed numbers to percentages: Mixed numbers (e.g., 2 1/4) require an extra step of converting them to improper fractions before applying the methods discussed above.
- Converting percentages to fractions and decimals: The reverse process is equally important and involves dividing the percentage by 100 to obtain the decimal equivalent and then simplifying the decimal to a fraction.
- Working with percentages greater than 100%: These represent values larger than the whole and require understanding the concept of proportions beyond a single unit.
Troubleshooting Common Mistakes
When converting fractions to percentages, common mistakes include:
- Incorrect division: Ensuring accurate division of the numerator by the denominator is crucial. Using a calculator can help minimize errors.
- Forgetting to multiply by 100: Remember that the decimal must be multiplied by 100 to express it as a percentage.
- Misinterpreting the fraction: Make sure you correctly identify the numerator and denominator before beginning the calculation.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with widespread applications. By understanding the various methods presented—converting to decimals, finding equivalent fractions, and using proportions—you can confidently tackle these conversions in various contexts. This skill enhances your ability to analyze data, understand financial concepts, and solve everyday problems involving proportions and ratios. Mastering this skill equips you with a valuable tool for navigating the numerical world effectively. Practice is key to solidifying your understanding and building confidence in your ability to perform these calculations accurately and efficiently. Remember to always double-check your work and utilize calculators or other tools to minimize errors, ensuring that your conversions are precise and reliable.
Latest Posts
Latest Posts
-
How Long Does It Take To Drive 2000 Miles
Jul 18, 2025
-
How Many Grams In A Teaspoon Of Cinnamon
Jul 18, 2025
-
How Long To Heat Water In Microwave
Jul 18, 2025
-
40 Oz Of Water Is How Many Cups
Jul 18, 2025
-
How Many Eighths In A Quarter Pound
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 12/25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.