What Is 12 Out Of 20 As A Percent
Kalali
Mar 06, 2025 · 5 min read
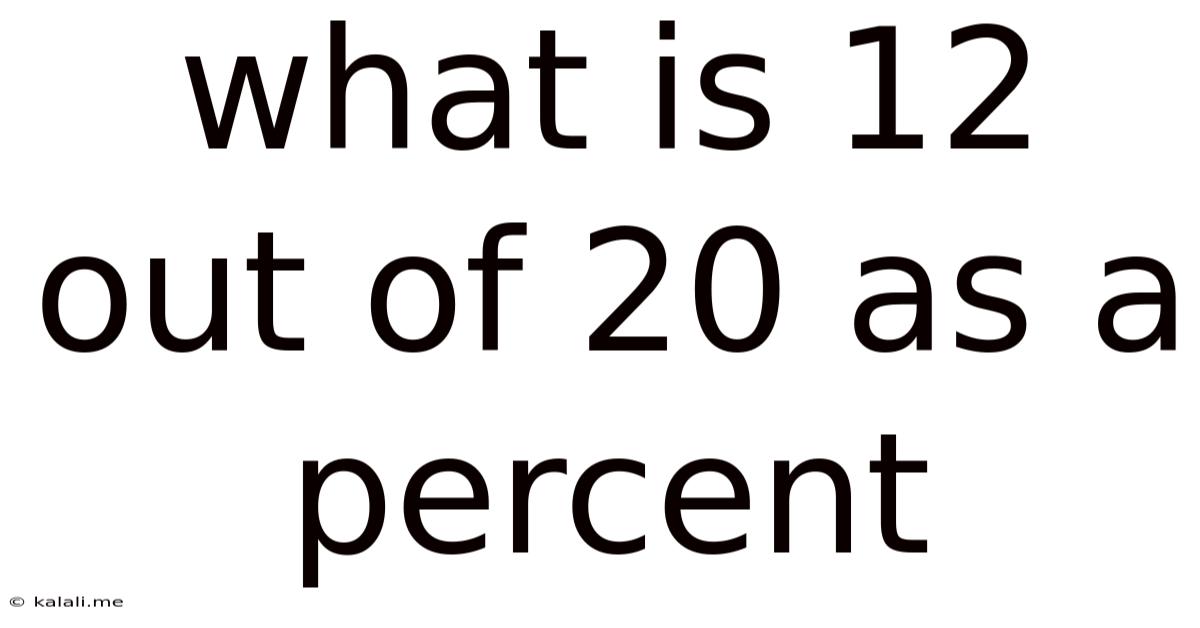
Table of Contents
What is 12 out of 20 as a Percent? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to express fractions as percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This comprehensive guide will delve into the process of calculating "12 out of 20 as a percent," providing a step-by-step explanation, exploring different calculation methods, and highlighting the broader significance of percentage calculations.
Understanding Percentages
A percentage is simply a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin phrase "per centum," meaning "out of a hundred." Therefore, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. Percentages provide a standardized and easily comparable way to represent proportions and ratios.
Calculating "12 out of 20" as a Percentage: The Basic Method
The most straightforward method for converting a fraction to a percentage involves two simple steps:
Step 1: Convert the Fraction to a Decimal
The fraction "12 out of 20" is written as 12/20. To convert this fraction to a decimal, simply divide the numerator (12) by the denominator (20):
12 ÷ 20 = 0.6
Step 2: Convert the Decimal to a Percentage
To express the decimal as a percentage, multiply it by 100 and add the "%" symbol:
0.6 x 100 = 60%
Therefore, 12 out of 20 is equal to 60%.
Alternative Methods for Percentage Calculation
While the basic method is efficient and easy to understand, alternative approaches can be equally effective depending on the context and individual preference. Let's explore some of these methods:
Method 2: Simplifying the Fraction First
Sometimes, simplifying the fraction before converting it to a decimal can make the calculation easier. In this case, we can simplify 12/20 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4:
12 ÷ 4 = 3 20 ÷ 4 = 5
This simplifies the fraction to 3/5. Now, we can convert 3/5 to a decimal:
3 ÷ 5 = 0.6
Then, convert the decimal to a percentage:
0.6 x 100 = 60%
This method demonstrates that simplifying the fraction beforehand can sometimes streamline the calculation.
Method 3: Using Proportions
Another approach involves setting up a proportion:
12/20 = x/100
To solve for x (the percentage), cross-multiply:
20x = 1200
Divide both sides by 20:
x = 60
Therefore, x = 60%, confirming our previous results. This method is particularly useful when dealing with more complex fractions or when understanding the underlying proportional relationships is important.
Practical Applications of Percentage Calculations
The ability to calculate percentages has numerous practical applications across various fields:
1. Finance and Budgeting:
- Interest rates: Understanding interest rates on loans, savings accounts, and investments requires proficiency in percentage calculations.
- Discounts and sales: Calculating discounts offered during sales or promotional events relies heavily on percentage calculations.
- Tax calculations: Determining the amount of tax payable on income, purchases, or property involves percentage calculations.
- Investment returns: Evaluating the performance of investments and calculating returns requires calculating percentage changes.
2. Data Analysis and Statistics:
- Representing proportions: Percentages provide a clear and concise way to represent proportions within datasets.
- Interpreting survey results: Analyzing survey data and interpreting results often involves converting frequencies to percentages.
- Calculating rates and ratios: Many statistical measures, such as growth rates and ratios, are expressed as percentages.
- Creating charts and graphs: Percentages are commonly used in creating charts and graphs to visually represent data.
3. Science and Engineering:
- Concentration calculations: Calculating the concentration of solutions in chemistry often involves percentages.
- Efficiency calculations: Determining the efficiency of machines or processes often relies on percentage calculations.
- Error analysis: Expressing errors or uncertainties in measurements often involves percentages.
4. Everyday Life:
- Tip calculations: Calculating tips in restaurants involves determining a percentage of the bill.
- Sales tax: Calculating sales tax on purchases requires knowing and applying the applicable percentage rate.
- Grading systems: Many grading systems in education use percentages to represent student performance.
- Comparing prices: Percentages help compare prices and find the best deals while shopping.
Common Mistakes to Avoid when Calculating Percentages
While percentage calculations are relatively straightforward, several common errors can lead to inaccurate results. Avoiding these pitfalls ensures accuracy:
- Incorrect order of operations: Remember to follow the order of operations (PEMDAS/BODMAS) when calculating percentages, especially when dealing with complex expressions.
- Misplacing the decimal point: Pay close attention to decimal places when converting between decimals and percentages. A misplaced decimal can lead to significant errors.
- Confusing percentage change with absolute change: Understand the difference between a percentage increase/decrease and the absolute increase/decrease. These are distinct concepts.
- Incorrect use of percentages in comparisons: Always ensure that comparisons using percentages are made with respect to the same base value. Comparing percentages from different bases can lead to misleading conclusions.
Expanding Your Understanding of Percentages: Advanced Concepts
Beyond the basic calculations, there are more advanced percentage concepts that are valuable to grasp:
- Percentage change: This involves calculating the percentage increase or decrease between two values. The formula is: [(New Value - Old Value) / Old Value] x 100%.
- Percentage points: This is a measure of the absolute difference between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
- Compound interest: This involves calculating interest on both the principal amount and accumulated interest. It's a crucial concept in finance and investments.
- Percentage points versus percent change: Understanding the distinction between these two is key to accurate interpretation of data.
Mastering these advanced concepts will significantly enhance your ability to analyze data, make informed financial decisions, and communicate numerical information effectively.
Conclusion: The Importance of Mastering Percentage Calculations
The ability to confidently and accurately calculate percentages is an invaluable skill in diverse settings. From everyday budgeting to complex financial analysis, understanding how to express fractions as percentages is crucial for interpreting data, making informed decisions, and effectively communicating numerical information. This guide provides a comprehensive approach to understanding and applying percentage calculations, emphasizing the importance of accuracy, and highlighting the numerous practical applications of this fundamental mathematical concept. By mastering these techniques, you can greatly improve your problem-solving skills and broaden your understanding of the world around you.
Latest Posts
Latest Posts
-
How Many Mikes Hard To Get Drunk
Jul 15, 2025
-
How Many Liters Has In Half Gallon
Jul 15, 2025
-
How Much Is Half Of A Mile
Jul 15, 2025
-
What Letter Is Halfway Through The Alphabet
Jul 15, 2025
-
How Many Cups Of Chocolate Chips In 4 Oz
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 Out Of 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.