What Is 14 Out Of 18 As A Percentage
Kalali
Apr 15, 2025 · 5 min read
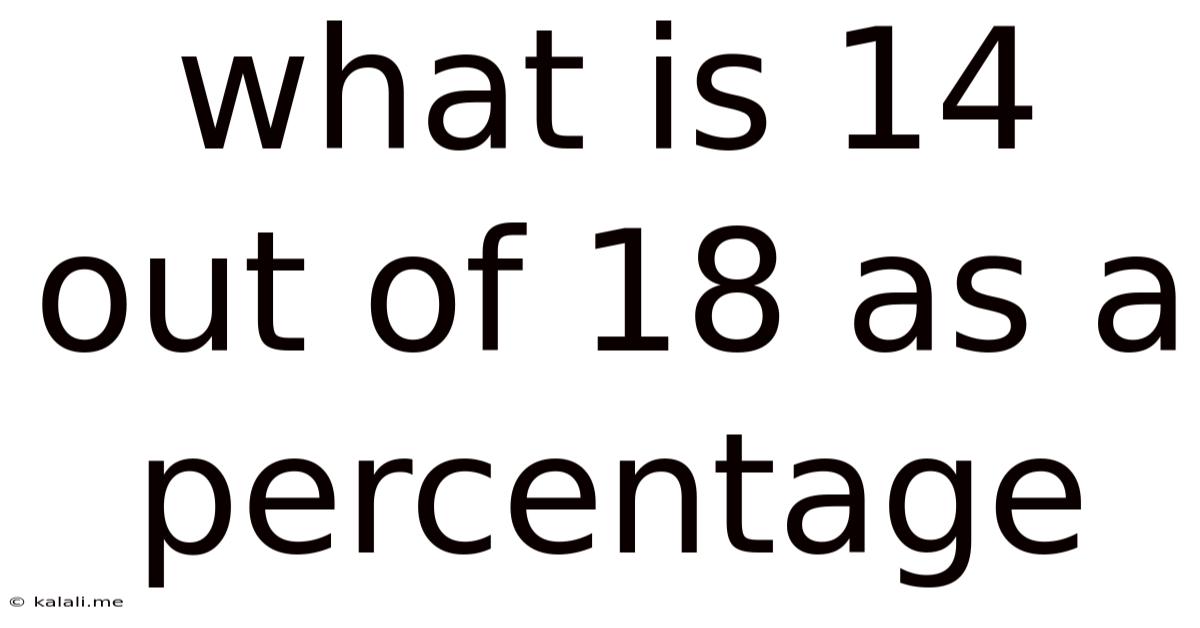
Table of Contents
- What Is 14 Out Of 18 As A Percentage
- Table of Contents
- What is 14 out of 18 as a Percentage? A Comprehensive Guide to Percentage Calculations
- Understanding Percentages
- Method 1: The Direct Conversion Method
- Method 2: Simplifying the Fraction First
- Method 3: Using Proportions
- Practical Applications of Percentage Calculations
- Common Mistakes to Avoid When Calculating Percentages
- Beyond the Basics: Percentage Increase and Decrease
- Advanced Percentage Calculations: Applications in Statistics and Data Analysis
- Conclusion: Mastering Percentage Calculations
- Latest Posts
- Latest Posts
- Related Post
What is 14 out of 18 as a Percentage? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with broad applications across various fields, from everyday budgeting and shopping to complex statistical analysis and scientific research. Understanding how to convert fractions to percentages is crucial for interpreting data, making informed decisions, and communicating numerical information effectively. This article will delve into the specifics of calculating "14 out of 18 as a percentage," exploring various methods and providing a broader understanding of percentage calculations. We'll also touch on practical applications and common mistakes to avoid.
Meta Description: Learn how to calculate 14 out of 18 as a percentage. This comprehensive guide covers various methods, explains the concept of percentages, and provides practical examples for everyday use. Master percentage calculations with ease!
Understanding Percentages
Before diving into the calculation, let's clarify what a percentage represents. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote a percentage. Essentially, it represents a portion of a whole. For example, 50% means 50 out of 100, or half.
Method 1: The Direct Conversion Method
This is the most straightforward approach to calculating "14 out of 18 as a percentage." We can express "14 out of 18" as a fraction: 14/18. To convert this fraction to a percentage, we follow these steps:
-
Divide the numerator by the denominator: 14 ÷ 18 ≈ 0.7778
-
Multiply the result by 100: 0.7778 x 100 ≈ 77.78
Therefore, 14 out of 18 is approximately 77.78%.
This method is efficient and easy to understand, making it suitable for quick calculations. However, rounding may be necessary, as most percentage calculations will not result in a whole number. In this case, we rounded to two decimal places for accuracy.
Method 2: Simplifying the Fraction First
An alternative approach involves simplifying the fraction before converting it to a percentage. This can sometimes make the division easier. Let's simplify 14/18:
Both 14 and 18 are divisible by 2, resulting in the simplified fraction 7/9.
Now, we repeat the process from Method 1:
-
Divide the numerator by the denominator: 7 ÷ 9 ≈ 0.7778
-
Multiply the result by 100: 0.7778 x 100 ≈ 77.78%
As you can see, we arrive at the same result: approximately 77.78%. Simplifying the fraction beforehand can be helpful, especially when dealing with larger numbers, but it's not strictly necessary.
Method 3: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion:
14/18 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', we cross-multiply:
18x = 1400
x = 1400/18
x ≈ 77.78
This method demonstrates the underlying mathematical principle behind percentage calculations. It's a more formal approach, suitable for understanding the fundamental concepts involved.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in many aspects of life:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns. Understanding percentage changes is crucial for tracking financial performance and making sound financial decisions.
-
Sales and Marketing: Determining conversion rates, customer acquisition costs, market share, and analyzing sales data. Marketing strategies often rely heavily on analyzing percentage changes to gauge effectiveness.
-
Education: Calculating grades, assessing student performance, and understanding statistical data related to education. Percentages are vital for representing academic achievements.
-
Science: Expressing experimental results, analyzing statistical data, and representing proportions in scientific studies. Scientific research frequently uses percentage calculations to communicate findings.
-
Everyday Life: Calculating tips, discounts at stores, understanding nutritional information on food labels, and interpreting various statistics in news reports. Percentages play a significant role in our daily decision-making processes.
Common Mistakes to Avoid When Calculating Percentages
Several common pitfalls can lead to inaccurate percentage calculations:
-
Incorrect order of operations: Always perform the division before multiplying by 100.
-
Rounding errors: While rounding is sometimes necessary, it's important to maintain sufficient precision to avoid significant errors, especially in financial calculations.
-
Confusing numerator and denominator: Ensure that the correct value represents the part and the whole. The "part" goes in the numerator, and the "whole" goes in the denominator.
-
Not converting to a decimal: Before multiplying by 100, ensure the fraction is first converted to a decimal by performing the division.
-
Using the wrong formula: Double-check your formula to ensure you are using the appropriate method for the specific problem.
Beyond the Basics: Percentage Increase and Decrease
Understanding how to calculate percentage increases and decreases is essential for many real-world applications. For example, calculating the percentage change in sales from one year to the next or determining the percentage discount applied to a product.
Percentage Increase: To calculate a percentage increase, subtract the original value from the new value, divide the result by the original value, and then multiply by 100.
Percentage Decrease: To calculate a percentage decrease, subtract the new value from the original value, divide the result by the original value, and then multiply by 100.
Advanced Percentage Calculations: Applications in Statistics and Data Analysis
Percentages are fundamental to many statistical concepts, including:
-
Proportions: Percentages are used to represent the proportion of a sample that falls into a particular category.
-
Probability: Percentages are used to express the probability of an event occurring.
-
Confidence Intervals: Percentages are used in constructing confidence intervals, which provide a range of values that are likely to contain the true population parameter.
-
Hypothesis Testing: Percentages are used in hypothesis testing to determine the statistical significance of results.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations opens doors to a deeper understanding of numerical data and its applications in various fields. Whether you're calculating discounts, analyzing sales data, or interpreting scientific findings, understanding how to convert fractions to percentages is a crucial skill. By understanding the various methods and avoiding common pitfalls, you can confidently navigate percentage calculations in both simple and complex scenarios. Remember to practice regularly and apply these techniques to real-world problems to solidify your understanding. The ability to work comfortably with percentages is a valuable asset in many aspects of life, both personal and professional.
Latest Posts
Latest Posts
-
How Much Is 240ml In Cups
Apr 26, 2025
-
How Many Feet Are In 50 In
Apr 26, 2025
-
250 Ml Of Water To Cups
Apr 26, 2025
-
How Many Cups Is 1 5 Pints
Apr 26, 2025
-
Do The Diagonals Of Rhombus Bisect The Angles
Apr 26, 2025
Related Post
Thank you for visiting our website which covers about What Is 14 Out Of 18 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.