What Is 15 16 As A Decimal
Kalali
Apr 08, 2025 · 6 min read
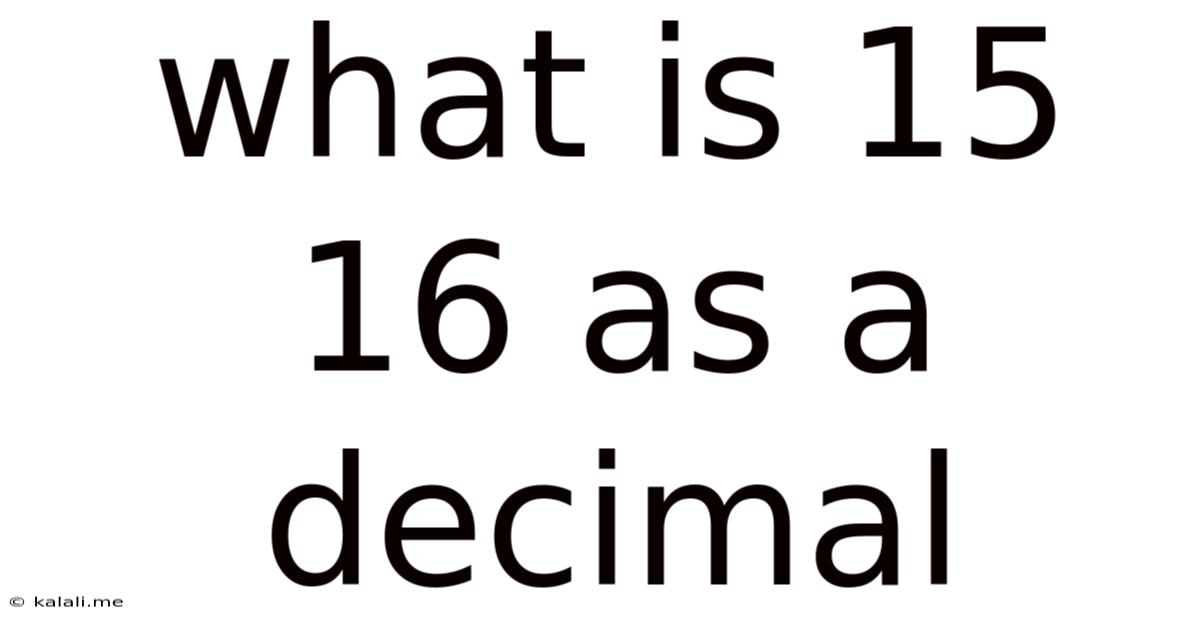
Table of Contents
What is 15/16 as a Decimal? A Comprehensive Guide to Fraction-to-Decimal Conversion
The question "What is 15/16 as a decimal?" might seem simple at first glance, but it opens the door to understanding a fundamental concept in mathematics: converting fractions to decimals. This seemingly straightforward task is crucial in various fields, from basic arithmetic to advanced scientific calculations and programming. This comprehensive guide will not only answer the initial question but will also delve into the underlying principles and provide you with the tools to tackle similar conversions with confidence.
Meta Description: Learn how to convert fractions to decimals. This guide comprehensively explains how to convert 15/16 to its decimal equivalent and provides various methods for similar conversions, covering both manual calculations and using technology.
Understanding Fractions and Decimals
Before diving into the conversion of 15/16, let's briefly revisit the concepts of fractions and decimals.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
A decimal is another way to represent a part of a whole. It uses a base-ten system, with digits placed to the right of a decimal point representing tenths, hundredths, thousandths, and so on. For example, 0.5 represents half (5 tenths), and 0.75 represents three-quarters (7 tenths and 5 hundredths).
Method 1: Long Division
The most fundamental method for converting a fraction to a decimal is through long division. We divide the numerator (15) by the denominator (16).
-
Set up the long division: Write 15 as the dividend (inside the division symbol) and 16 as the divisor (outside the division symbol). Since 15 is smaller than 16, we add a decimal point to 15 and add a zero to make it 15.0. This doesn't change the value; it simply allows us to perform the division.
-
Perform the division: 16 goes into 15 zero times, so we place a 0 above the decimal point. Then, we bring down the 0, making it 150. 16 goes into 150 nine times (16 x 9 = 144). Subtract 144 from 150, leaving a remainder of 6.
-
Continue the process: Add another zero to the remainder (60) and continue the division. 16 goes into 60 three times (16 x 3 = 48). Subtract 48 from 60, leaving a remainder of 12.
-
Repeat as needed: Add another zero (120). 16 goes into 120 seven times (16 x 7 = 112). Subtract 112 from 120, leaving a remainder of 8.
-
Further Iteration: Continue this process. Adding another zero (80), 16 goes into 80 five times (16 x 5 = 80). The remainder is 0, indicating the division is complete.
Therefore, 15/16 = 0.9375
This long division method, while slightly time-consuming, provides a clear and step-by-step understanding of the conversion process. It's a valuable skill to master for understanding the underlying mathematical principle.
Method 2: Converting to an Equivalent Fraction with a Denominator of 10, 100, 1000, etc.
This method is particularly useful when the denominator of the fraction is a factor of a power of 10. Unfortunately, 16 is not a direct factor of 10, 100, 1000, etc. However, we can explore this method for fractions where it's applicable. For example, if we had 5/8, we could convert it to 625/1000 by multiplying both the numerator and the denominator by 125. This easily converts to 0.625.
While not directly applicable to 15/16, understanding this method highlights the importance of finding common factors and simplifies conversion when possible.
Method 3: Using a Calculator
The simplest and often quickest way to convert 15/16 to a decimal is using a calculator. Simply enter "15 ÷ 16" and the calculator will display the decimal equivalent: 0.9375. This method is efficient for quick conversions, but it's important to understand the underlying mathematical principles for more complex scenarios or situations where a calculator isn't available.
Understanding the Decimal Result: 0.9375
The decimal representation 0.9375 confirms that 15/16 represents a value slightly less than 1 (a whole). This makes intuitive sense, as 15 is close to 16. The decimal accurately reflects the proportional value of 15 parts out of a total of 16 parts.
Practical Applications
The ability to convert fractions to decimals is essential in numerous real-world situations:
-
Financial Calculations: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals.
-
Scientific Measurements: Many scientific measurements and calculations require decimal representations for accuracy and ease of manipulation.
-
Engineering and Design: Precision in engineering and design relies heavily on decimal calculations.
-
Computer Programming: Many programming languages require decimal representations for numerical computations.
-
Everyday Life: From calculating tips to measuring ingredients in recipes, understanding decimal equivalents of fractions is frequently useful.
Converting Other Fractions: A Step-by-Step Approach
Let's solidify your understanding by applying the methods described above to convert some other fractions to decimals:
Example 1: Converting 7/8 to a decimal:
-
Long Division: Divide 7 by 8. You'll find that 7/8 = 0.875.
-
Equivalent Fraction: 7/8 can be converted to 875/1000 (by multiplying numerator and denominator by 125), which easily converts to 0.875.
-
Calculator: A calculator will quickly confirm that 7/8 = 0.875.
Example 2: Converting 3/5 to a decimal:
-
Long Division: Dividing 3 by 5 gives 0.6.
-
Equivalent Fraction: 3/5 can be easily converted to 6/10 by multiplying both the numerator and denominator by 2. This directly translates to 0.6.
-
Calculator: The calculator will quickly show the result as 0.6.
Example 3: Converting 1/3 to a decimal:
This example highlights a crucial point: not all fractions convert to terminating decimals. When you divide 1 by 3, you get a repeating decimal: 0.3333... This is represented as 0.3̅. The bar above the 3 indicates that the digit 3 repeats infinitely.
Conclusion
Converting fractions to decimals is a fundamental mathematical skill with broad applications. While calculators provide a quick and easy method, understanding the underlying principles, particularly long division and equivalent fractions, offers a deeper understanding of the mathematical concepts involved. Mastering these techniques empowers you to handle various mathematical challenges efficiently and confidently, regardless of the tools available. Remember to practice different examples to build your proficiency and always double-check your work, especially when dealing with precision in scientific or financial contexts.
Latest Posts
Latest Posts
-
What Is A Statement Of Proportionality
Apr 17, 2025
-
How Much Is 84 In In Feet
Apr 17, 2025
-
What Is The Lowest Common Multiple Of 3 And 7
Apr 17, 2025
-
2 To The Power Of 40
Apr 17, 2025
-
Cuanto Son 73 Grados Fahrenheit En Centigrados
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 16 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.