What Is 15 Out Of 20 As A Percentage
Kalali
Apr 16, 2025 · 5 min read
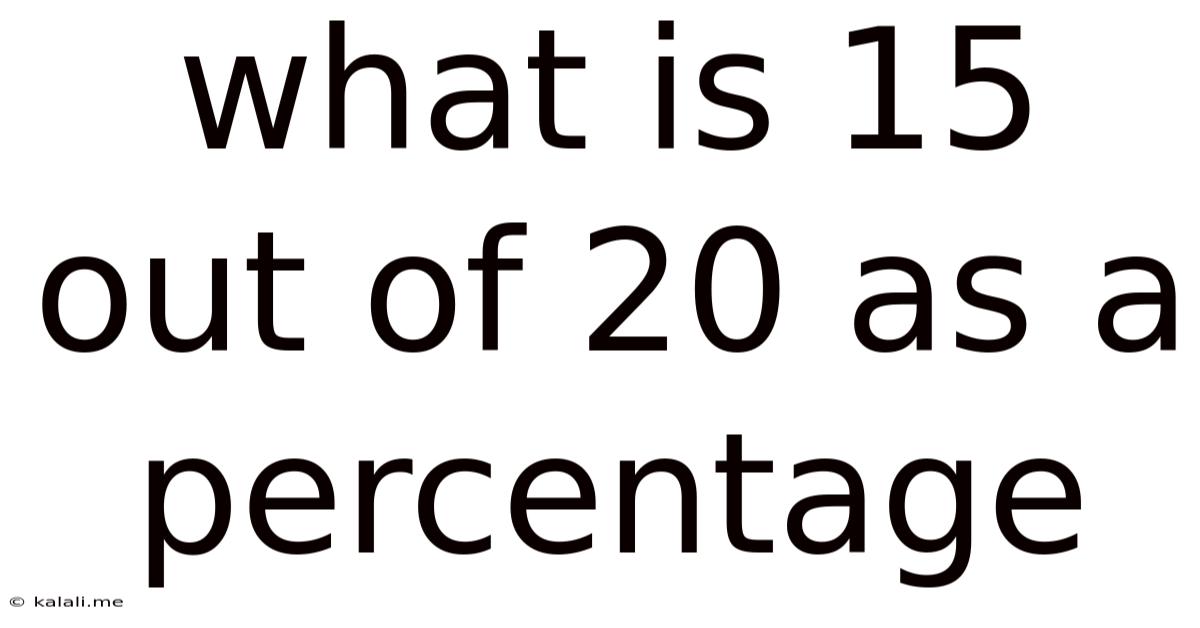
Table of Contents
What is 15 out of 20 as a Percentage? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and tax to analyzing data and understanding statistics. This article will delve deep into the question, "What is 15 out of 20 as a percentage?", providing not only the answer but also a comprehensive explanation of the process and its applications. We'll explore different methods for calculating percentages, discuss common percentage-related problems, and offer practical examples to solidify your understanding. This guide aims to equip you with the knowledge to confidently tackle any percentage calculation you encounter.
Meta Description: Learn how to calculate percentages effortlessly! This comprehensive guide explains how to find 15 out of 20 as a percentage and provides various methods and examples for mastering percentage calculations.
Understanding Percentages: The Basics
A percentage represents a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, any percentage can be expressed as a fraction with a denominator of 100. For instance, 50% is the same as 50/100, which simplifies to 1/2.
Percentages are used extensively because they offer a standardized way to compare different proportions. Whether it's comparing test scores, sales figures, or growth rates, percentages provide a consistent and easily understandable metric.
Calculating "15 out of 20" as a Percentage: The Primary Method
The most straightforward method to calculate "15 out of 20" as a percentage involves the following steps:
-
Form a fraction: Express the given numbers as a fraction. In this case, it's 15/20.
-
Convert to a decimal: Divide the numerator (15) by the denominator (20): 15 ÷ 20 = 0.75
-
Multiply by 100: Multiply the decimal by 100 to convert it to a percentage: 0.75 × 100 = 75
-
Add the percentage symbol: The final answer is 75%. Therefore, 15 out of 20 is equal to 75%.
Alternative Methods for Percentage Calculation
While the primary method is the most common and generally easiest to understand, several alternative methods can be used to arrive at the same result. Understanding these alternative approaches can broaden your mathematical toolkit and help you choose the most efficient method depending on the context.
Method 2: Using Proportions
This method leverages the concept of proportions. We know that x/100 represents the percentage we're looking for. We can set up a proportion:
15/20 = x/100
Cross-multiply: 20x = 1500
Solve for x: x = 1500/20 = 75
Therefore, x = 75%, confirming our previous result. This method is particularly useful when dealing with more complex percentage problems.
Method 3: Simplifying the Fraction First
Before converting to a decimal, we can simplify the fraction 15/20. Both the numerator and the denominator are divisible by 5:
15/20 = 3/4
Now, convert the simplified fraction to a decimal: 3 ÷ 4 = 0.75
Multiply by 100 to get the percentage: 0.75 × 100 = 75%
Simplifying the fraction first can make the subsequent calculations easier, especially when dealing with larger numbers.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in a multitude of real-world scenarios. Here are a few examples:
-
Academic Performance: Calculating grades, class averages, and overall GPA often involves percentage calculations. For instance, if a student scores 15 out of 20 on a quiz, their score is 75%.
-
Financial Matters: Percentages are vital in finance for calculating interest rates, discounts, taxes, profits, and losses. For example, a 20% discount on a $100 item would reduce the price by $20.
-
Data Analysis: Percentages are extensively used to represent data in charts, graphs, and reports. They help to visualize proportions and trends within datasets. For example, analyzing market share often involves working with percentages.
-
Sales and Marketing: Tracking conversion rates, customer acquisition costs, and return on investment (ROI) heavily relies on percentage calculations.
-
Cooking and Baking: Many recipes use percentages when specifying ingredient quantities.
Dealing with More Complex Percentage Problems
While the "15 out of 20" example is relatively straightforward, percentage calculations can become more complex. Let's explore some scenarios:
-
Finding a percentage of a number: For example, finding 25% of 80. This involves multiplying 80 by 0.25 (which is 25/100), resulting in 20.
-
Finding the original number when a percentage is known: For instance, if 15% of a number is 30, what is the number? This requires setting up an equation: 0.15x = 30. Solving for x gives you 200.
-
Calculating percentage increase or decrease: For example, if a price increases from $50 to $60, the percentage increase is calculated as ((60-50)/50) x 100 = 20%.
Common Mistakes to Avoid When Calculating Percentages
Several common mistakes can lead to inaccurate percentage calculations. Be mindful of these:
-
Incorrect order of operations: Remember the order of operations (PEMDAS/BODMAS). Incorrect sequencing of multiplication and division can lead to errors.
-
Decimal point errors: Misplacing decimal points during calculations is a frequent source of errors. Double-check your work carefully.
-
Confusion with fractions and decimals: Make sure you understand the correct conversions between fractions, decimals, and percentages.
Practicing Percentage Calculations: Tips and Tricks
Regular practice is key to mastering percentage calculations. Here are some tips:
-
Start with simple problems: Begin with easy examples before tackling more complex ones.
-
Use different methods: Practice using various methods (like the ones described above) to build a versatile understanding.
-
Check your answers: Always verify your answers to ensure accuracy.
-
Use online calculators (for verification only): Online calculators can be helpful for checking your work but don't rely on them for learning the underlying concepts.
Conclusion: Mastering Percentages for Everyday Life
Understanding how to calculate percentages is a valuable skill with wide-ranging applications in daily life. By grasping the fundamental methods, practicing regularly, and avoiding common pitfalls, you can confidently handle various percentage-related problems. This article provided a comprehensive guide, moving from the simple calculation of "15 out of 20 as a percentage" to more complex scenarios and practical applications. Remember that the key to mastering percentages lies in consistent practice and a thorough understanding of the underlying principles. With this knowledge, you are well-equipped to tackle any percentage calculation you may encounter.
Latest Posts
Latest Posts
-
How Many Feet In 13 Meters
Apr 16, 2025
-
What Percentage Is 3 Out Of 4
Apr 16, 2025
-
What Is The Least Common Multiple Of 5 And 15
Apr 16, 2025
-
What Is The Decimal For 7 10
Apr 16, 2025
-
How Many Centimeters In 62 Inches
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Out Of 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.