What Is 15 Percent Of 20
Kalali
Apr 07, 2025 · 5 min read
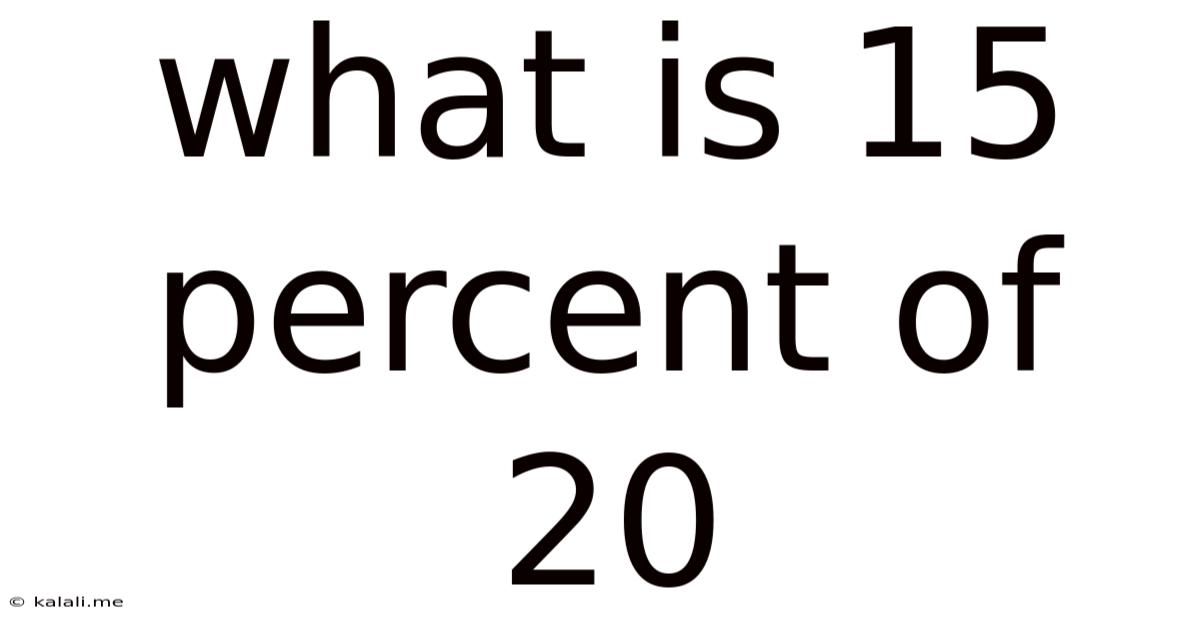
Table of Contents
- What Is 15 Percent Of 20
- Table of Contents
- What is 15 Percent of 20? A Deep Dive into Percentage Calculations
- Understanding Percentages: The Foundation
- Converting Percentages to Decimals and Fractions:
- Calculating 15% of 20: Three Proven Methods
- Method 1: Using the Decimal Equivalent
- Method 2: Using the Fraction Equivalent
- Method 3: Proportion Method (Cross-Multiplication)
- Real-World Applications of Percentage Calculations
- Finance and Budgeting:
- Sales and Marketing:
- Data Analysis and Statistics:
- Advanced Percentage Calculations: Beyond the Basics
- Finding the Percentage:
- Finding the Original Number:
- Percentage Increase and Decrease:
- Conclusion: Mastering Percentage Calculations
- Latest Posts
- Latest Posts
- Related Post
What is 15 Percent of 20? A Deep Dive into Percentage Calculations
The seemingly simple question, "What is 15 percent of 20?" opens the door to a fascinating exploration of percentages, their applications, and the underlying mathematical principles. While the answer itself is easily calculated, understanding the why behind the calculation is crucial for applying percentage concepts in various real-world scenarios, from budgeting and finance to sales and statistics. This comprehensive guide will delve into the calculation, explore different methods, and showcase the broader significance of percentage calculations.
Understanding Percentages: The Foundation
Before we tackle the specific problem, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. This fundamental understanding is key to solving any percentage problem.
Converting Percentages to Decimals and Fractions:
To perform calculations effectively, it's often beneficial to convert percentages into their decimal or fractional equivalents. This makes the arithmetic much simpler.
-
Percentage to Decimal: To convert a percentage to a decimal, divide the percentage by 100. For example, 15% becomes 15/100 = 0.15.
-
Percentage to Fraction: To convert a percentage to a fraction, write the percentage as the numerator and 100 as the denominator. Then, simplify the fraction if possible. For example, 15% becomes 15/100, which simplifies to 3/20.
Calculating 15% of 20: Three Proven Methods
Now, let's address the core question: what is 15% of 20? We'll explore three distinct methods to arrive at the solution:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We'll convert the percentage to its decimal equivalent and then multiply it by the number.
- Convert the percentage to a decimal: 15% = 0.15
- Multiply the decimal by the number: 0.15 * 20 = 3
Therefore, 15% of 20 is 3.
Method 2: Using the Fraction Equivalent
This method involves converting the percentage to a fraction, and then multiplying it by the number.
- Convert the percentage to a fraction: 15% = 15/100 = 3/20
- Multiply the fraction by the number: (3/20) * 20 = 3
Again, we arrive at the answer: 15% of 20 is 3. Note how the 20s cancel out in this method, simplifying the calculation.
Method 3: Proportion Method (Cross-Multiplication)
This method is particularly useful for solving more complex percentage problems. It uses proportions to find the unknown value.
We set up a proportion:
- Part/Whole = Percentage/100
In our case:
- x/20 = 15/100
To solve for x (15% of 20), we cross-multiply:
- 100x = 15 * 20
- 100x = 300
- x = 300/100
- x = 3
Once again, the answer is 3.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable across a multitude of disciplines. Here are a few examples:
Finance and Budgeting:
- Interest Calculations: Understanding percentages is essential for calculating simple and compound interest on loans, savings accounts, and investments.
- Tax Calculations: Calculating income tax, sales tax, and other taxes relies heavily on percentage calculations.
- Discounts and Sales: Determining the final price after a percentage discount requires understanding percentage reductions.
- Profit Margins: Businesses utilize percentages to calculate profit margins, understand their profitability, and make informed pricing decisions.
Sales and Marketing:
- Conversion Rates: Marketing professionals track conversion rates (e.g., website visitors who make a purchase) as percentages to measure campaign effectiveness.
- Market Share: Companies use percentages to represent their share of a particular market.
- Sales Growth: Percentage change calculations show sales growth or decline over time.
Data Analysis and Statistics:
- Statistical Analysis: Percentages are fundamental in many statistical analyses, helping to represent data proportions and trends.
- Data Representation: Graphs and charts often utilize percentages to visualize data more effectively.
Advanced Percentage Calculations: Beyond the Basics
While our focus has been on a simple calculation, let's touch upon more complex percentage problems that build upon the fundamental concepts.
Finding the Percentage:
Instead of finding a percentage of a number, you might need to find what percentage one number is of another. For example: "What percentage of 20 is 6?" This requires setting up a proportion:
- x/100 = 6/20
Solving for x will reveal the percentage.
Finding the Original Number:
Another common problem involves finding the original number when you know a percentage and its resulting value. For example: "20 is 40% of what number?" This also requires setting up a proportion:
- 20/x = 40/100
Solving for x will give you the original number.
Percentage Increase and Decrease:
Calculating percentage increases and decreases is vital for tracking changes in values over time. For instance, if a value increases from 20 to 25, the percentage increase is calculated as:
- [(25 - 20) / 20] * 100% = 25%
Conclusion: Mastering Percentage Calculations
The seemingly simple problem of determining 15% of 20 serves as a gateway to a world of percentage calculations with diverse applications. By understanding the underlying principles, mastering the various methods of calculation, and appreciating the practical implications, you'll gain a valuable skill applicable across numerous fields. From personal finance to advanced statistical analysis, the ability to confidently work with percentages empowers you to make informed decisions and better understand the numerical world around you. The more you practice these calculations, the more intuitive and effortless they will become, allowing you to confidently tackle complex percentage problems with ease.
Latest Posts
Latest Posts
-
1 2 Cup Of Water To Ml
Apr 11, 2025
-
What Is A 29 Out Of 40
Apr 11, 2025
-
8 5 Inches Is How Many Cm
Apr 11, 2025
-
Fish That Have Fins And Scales
Apr 11, 2025
-
10 3 As A Mixed Number
Apr 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.