What Is 15 Percent Of 500
Kalali
Apr 13, 2025 · 5 min read
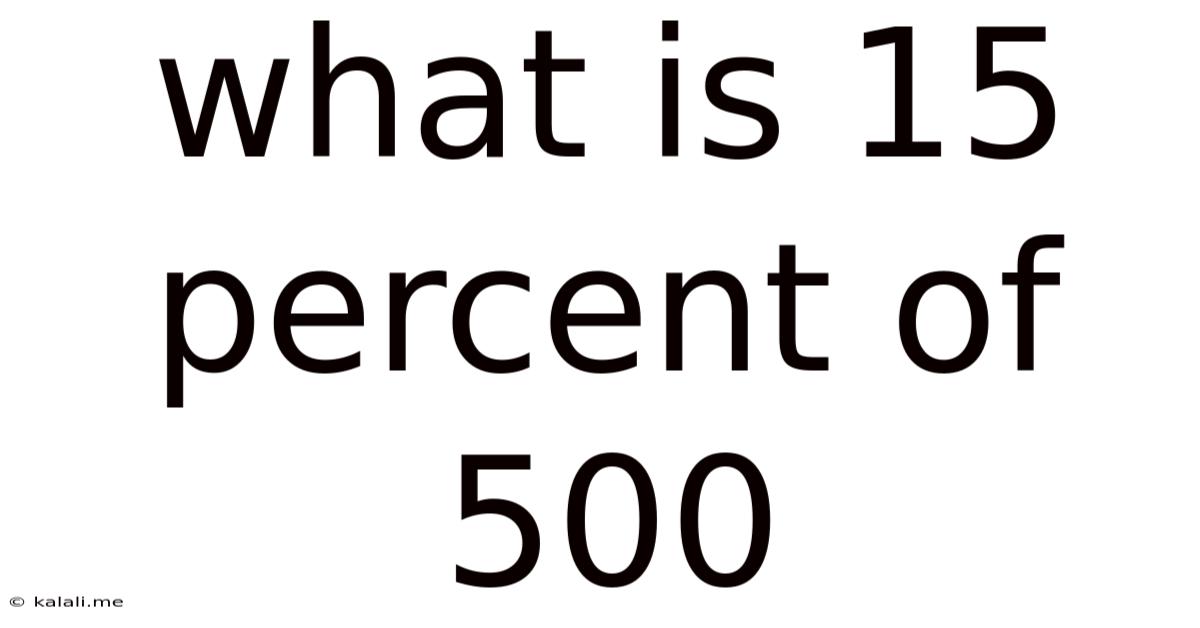
Table of Contents
What is 15 Percent of 500? A Deep Dive into Percentage Calculations and Their Applications
Finding 15 percent of 500 might seem like a simple calculation, suitable only for elementary school. However, understanding how to solve this problem unlocks a world of practical applications in various fields, from budgeting and finance to sales and data analysis. This article will not only provide the answer but delve into the multiple ways to calculate percentages, explain the underlying concepts, and explore real-world examples where this type of calculation proves invaluable.
Meta Description: Learn how to calculate 15% of 500 using different methods, understand the underlying principles of percentage calculations, and explore real-world applications in finance, sales, and more. This comprehensive guide clarifies percentage calculations for all skill levels.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 15% means 15 out of 100, which can be written as the fraction 15/100 or the decimal 0.15. This fundamental understanding is key to solving percentage problems.
Method 1: Using the Fraction Method
The most straightforward method involves converting the percentage to a fraction and then multiplying it by the whole number. In this case:
- Convert the percentage to a fraction: 15% = 15/100
- Multiply the fraction by the whole number: (15/100) * 500
Simplifying the calculation:
(15/100) * 500 = (15 * 500) / 100 = 7500 / 100 = 75
Therefore, 15% of 500 is 75.
Method 2: Using the Decimal Method
This method involves converting the percentage to a decimal and then multiplying it by the whole number.
- Convert the percentage to a decimal: 15% = 0.15
- Multiply the decimal by the whole number: 0.15 * 500 = 75
Again, we arrive at the answer: 15% of 500 is 75. This method is often preferred for its efficiency, particularly when using calculators.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between percentages and whole numbers. We set up a proportion:
- Part / Whole = Percentage / 100
In this case:
- x / 500 = 15 / 100
To solve for x (15% of 500), we cross-multiply:
100x = 15 * 500
100x = 7500
x = 7500 / 100
x = 75
This confirms that 15% of 500 is 75. The proportion method offers a more visual representation of the percentage relationship.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-life scenarios:
-
Finance: Calculating interest on loans, savings accounts, and investments. For instance, if you have a savings account with a 5% annual interest rate and a balance of $500, you can calculate your annual interest earned using percentage calculations. Discounts and sales tax are other examples that frequently use percentages.
-
Sales and Marketing: Determining discounts and profit margins. Retailers frequently offer percentage-based discounts (e.g., a 20% off sale). Calculating the final price after a discount requires understanding percentage calculations. Businesses also analyze sales data using percentages to track performance and identify trends. Conversion rates (the percentage of website visitors who make a purchase) are another critical metric.
-
Data Analysis: Representing data as percentages in charts and graphs for better visualization and interpretation. Percentages are essential in creating visually appealing and informative data representations. They are also used to calculate statistical measures and conduct various analyses.
-
Everyday Life: Calculating tips in restaurants, splitting bills, or determining the percentage of a certain ingredient in a recipe. These daily situations require an understanding of basic percentage calculations.
Advanced Percentage Calculations: Solving for the Whole or Percentage
While this article primarily focuses on calculating a percentage of a whole number, understanding how to solve for the whole or the percentage itself is equally important.
- Finding the Whole: If you know a part and the percentage, you can calculate the whole. For example, if 75 represents 15% of a certain number, you can set up an equation:
0.15 * x = 75
x = 75 / 0.15
x = 500
This demonstrates that 75 is 15% of 500.
- Finding the Percentage: If you know the part and the whole, you can calculate the percentage. For example, if you have 75 out of 500, you would calculate the percentage as:
(75 / 500) * 100 = 15%
Tips and Tricks for Efficient Percentage Calculations
-
Mental Math: For simple percentages like 10%, 20%, or 50%, mental calculation is often possible. 10% is simply moving the decimal point one place to the left. 50% is halving the number.
-
Using a Calculator: For more complex calculations or larger numbers, a calculator is a valuable tool. Most calculators have a percentage function (%) that simplifies the calculation process.
-
Breaking Down Percentages: Complex percentages can be broken down into simpler ones. For example, 15% can be thought of as 10% + 5%. Calculating 10% and 5% separately and adding the results can be easier than calculating 15% directly.
Conclusion: Mastering Percentage Calculations for Success
Understanding how to calculate percentages, and specifically, how to determine what 15 percent of 500 is, opens doors to a wider understanding of quantitative concepts. This seemingly basic calculation has profound applications across various disciplines, from personal finance management to complex data analysis. By mastering these techniques and employing different methods, individuals can confidently navigate numerical problems and make informed decisions in their personal and professional lives. The ability to perform percentage calculations efficiently and accurately is a valuable skill that enhances problem-solving capabilities and contributes to success in many aspects of life. This comprehensive guide equips you with the knowledge and tools to tackle percentage calculations with confidence and ease. Remember that practice is key to mastering this fundamental mathematical concept.
Latest Posts
Latest Posts
-
What Year Would I Be Born If I Was 17
Jul 15, 2025
-
What Is Longer A Kilometer Or A Mile
Jul 15, 2025
-
How Much Does A Full 15 Lb Propane Tank Weigh
Jul 15, 2025
-
Did Chester Wear A Brace On Gunsmoke
Jul 15, 2025
-
How Many Mikes Hard To Get Drunk
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.