What Is 16/20 As A Percent
Kalali
Apr 04, 2025 · 4 min read
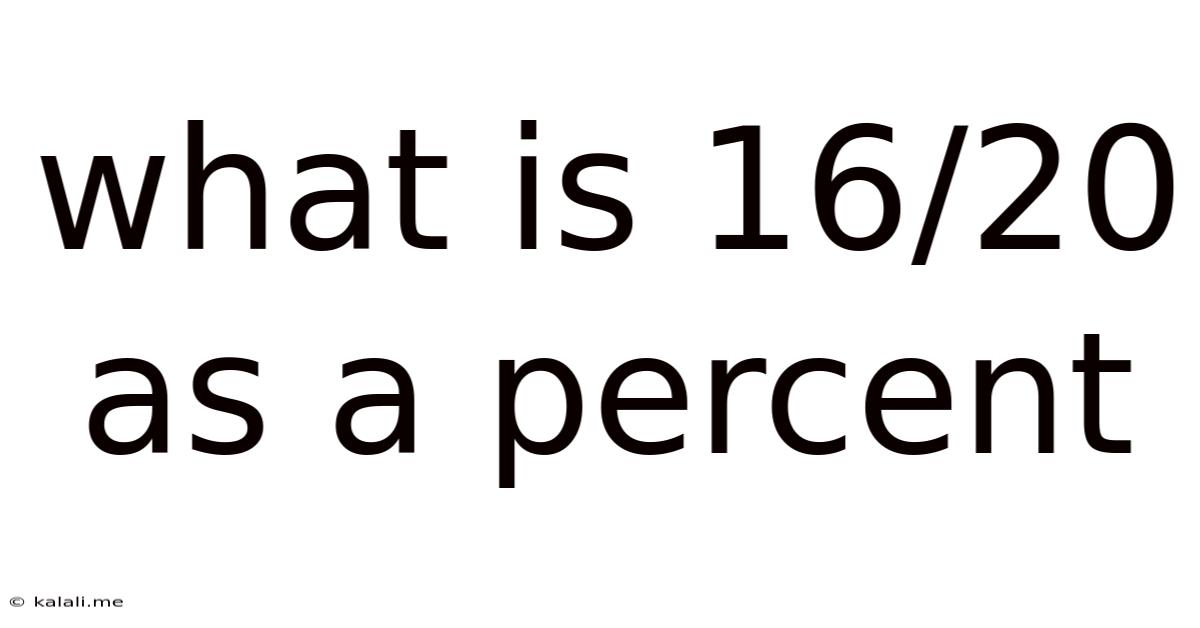
Table of Contents
What is 16/20 as a Percent? A Comprehensive Guide to Percentage Conversions
Converting fractions to percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and grades to understanding financial statements and statistical data. This comprehensive guide will delve into the process of converting the fraction 16/20 into a percentage, exploring various methods and providing a deeper understanding of the underlying principles. We'll also touch upon related concepts and offer practical examples to solidify your grasp of this essential mathematical operation.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts in the whole. In the fraction 16/20, 16 is the numerator and 20 is the denominator. This means we have 16 parts out of a total of 20 parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, or 50/100. Percentages are widely used to represent proportions, rates, and changes in various contexts.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 16/20 to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (16) by the denominator (20): 16 ÷ 20 = 0.8
-
Multiply the decimal by 100: 0.8 x 100 = 80
Therefore, 16/20 is equal to 80%.
Method 2: Simplifying the Fraction First
Before converting to a decimal, we can simplify the fraction 16/20 by finding the greatest common divisor (GCD) of 16 and 20. The GCD is 4. Dividing both the numerator and denominator by 4, we get:
16 ÷ 4 = 4 20 ÷ 4 = 5
This simplifies the fraction to 4/5. Now, we can convert 4/5 to a percentage using the same two-step process as Method 1:
-
Convert the simplified fraction to a decimal: 4 ÷ 5 = 0.8
-
Multiply the decimal by 100: 0.8 x 100 = 80
Again, we arrive at the answer: 16/20 is equal to 80%. Simplifying the fraction first can make the division easier, especially when dealing with larger numbers.
Method 3: Using Proportions
Another approach involves setting up a proportion. We want to find the percentage (x) that corresponds to 16 out of 20. We can set up the proportion as follows:
16/20 = x/100
To solve for x, we cross-multiply:
20x = 1600
Divide both sides by 20:
x = 80
Therefore, 16/20 is equal to 80%. This method is particularly useful for understanding the underlying relationship between fractions and percentages.
Practical Applications of Percentage Conversions
Understanding percentage conversions is crucial in various real-world scenarios:
-
Calculating Grades: If you answered 16 out of 20 questions correctly on a test, your score is 80%.
-
Determining Discounts: A 20% discount on a $100 item means you save $20 (20% of $100).
-
Analyzing Financial Statements: Companies use percentages to represent profit margins, revenue growth, and other key financial metrics.
-
Interpreting Statistical Data: Percentages are widely used in statistics to represent proportions and probabilities.
-
Understanding Interest Rates: Interest rates on loans and savings accounts are usually expressed as percentages.
Beyond 16/20: Generalizing the Conversion Process
The methods described above can be applied to convert any fraction to a percentage. The general formula is:
(Numerator / Denominator) * 100 = Percentage
For example, to convert 3/4 to a percentage:
(3/4) * 100 = 75%
Similarly, to convert 7/8 to a percentage:
(7/8) * 100 = 87.5%
Common Mistakes to Avoid
When converting fractions to percentages, it's important to avoid these common pitfalls:
-
Forgetting to multiply by 100: Remember that percentages are always expressed out of 100. Failing to multiply the decimal by 100 will result in an incorrect answer.
-
Incorrectly simplifying fractions: Ensure you simplify fractions correctly before converting them to decimals. An incorrect simplification will lead to an inaccurate percentage.
-
Rounding errors: When dealing with decimals that don't terminate, be mindful of rounding errors. Round to the appropriate number of decimal places based on the context.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with wide-ranging applications. Understanding the different methods, including direct conversion, simplification, and using proportions, provides flexibility and allows you to choose the most efficient approach based on the specific fraction. By mastering this skill, you'll be better equipped to handle various mathematical problems encountered in daily life, academic settings, and professional careers. Remember to practice regularly and avoid common errors to build confidence and proficiency in percentage conversions. This will significantly enhance your ability to analyze data, interpret information, and make informed decisions in various contexts.
Latest Posts
Latest Posts
-
How Tall Is 59 Inches In Ft
Apr 10, 2025
-
What Is The Factorization Of 49
Apr 10, 2025
-
How Many Inches Is 169 Cm
Apr 10, 2025
-
1 Cup Of Butter Is How Many Ounces
Apr 10, 2025
-
What The Average Height For A 14 Year Old
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 16/20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.