What Is 16 Out Of 20 As A Percent
Kalali
Mar 09, 2025 · 5 min read
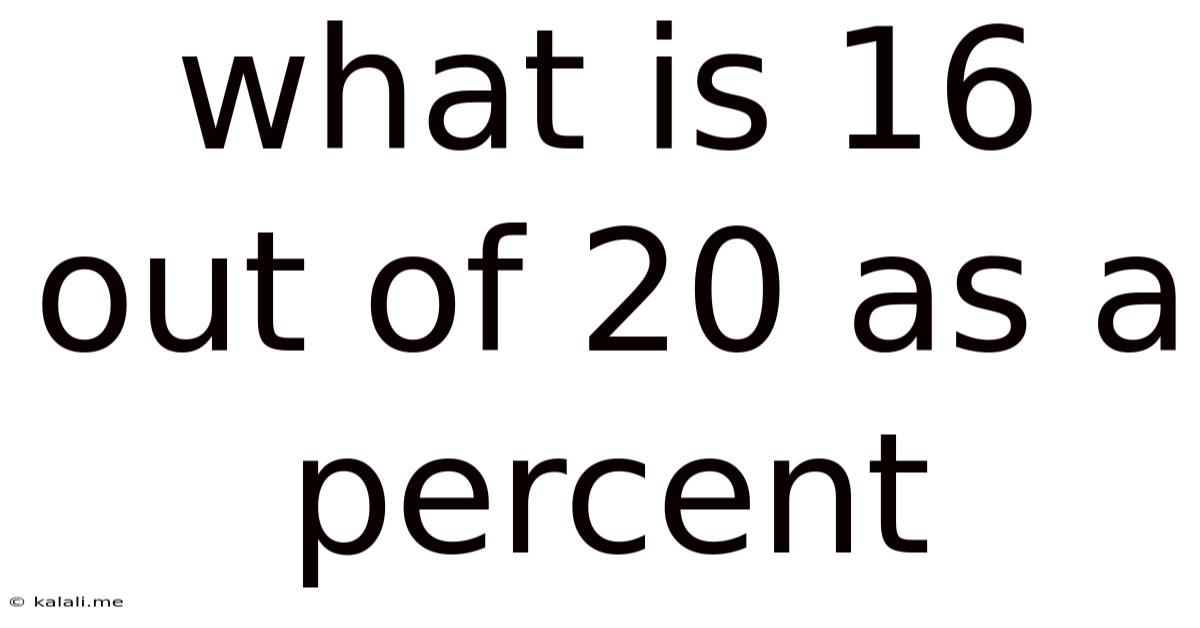
Table of Contents
What is 16 out of 20 as a Percent? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from academic studies and professional careers to everyday financial management and personal decision-making. Understanding how to express fractions as percentages allows for easier comparison and interpretation of data. This comprehensive guide will delve into the question "What is 16 out of 20 as a percent?" and provide a thorough understanding of the process, including various methods and real-world examples.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ("per" meaning "for each" and "cent" referring to "hundred"). Therefore, 16 out of 20 represents a portion of a whole, and converting it to a percentage allows us to express that portion in terms of 100.
Calculating 16 out of 20 as a Percentage: The Basic Method
The most straightforward way to calculate 16 out of 20 as a percentage is using the following formula:
(Part / Whole) * 100%
In this case:
- Part: 16
- Whole: 20
Substituting the values into the formula, we get:
(16 / 20) * 100% = 80%
Therefore, 16 out of 20 is equal to 80%.
Alternative Methods for Percentage Calculation
While the above method is the most common and readily understood, there are alternative approaches that can be helpful depending on the context and individual preference.
Method 2: Simplifying the Fraction
Before applying the percentage formula, we can simplify the fraction 16/20 by finding the greatest common divisor (GCD) of both numbers. The GCD of 16 and 20 is 4. Dividing both the numerator and denominator by 4, we get:
16/20 = 4/5
Now, converting 4/5 to a percentage:
(4 / 5) * 100% = 80%
This method reduces the calculation's complexity by simplifying the fraction first.
Method 3: Using Proportions
Proportions offer a slightly different perspective on the problem. We can set up a proportion to solve for the percentage:
16/20 = x/100
Cross-multiplying, we get:
20x = 1600
Dividing both sides by 20:
x = 80
Therefore, x = 80%, confirming our previous results. This method is particularly useful when dealing with more complex percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in various real-world scenarios. Here are a few examples:
1. Academic Performance
Imagine a student scores 16 out of 20 on a test. Converting this score to a percentage (80%) provides a standardized way to assess their performance relative to the total possible marks. This allows for easy comparison with other students and helps track academic progress.
2. Financial Calculations
Percentages are fundamental in financial calculations. For instance, calculating interest rates, discounts, tax amounts, profit margins, and investment returns all involve percentage calculations. Understanding these calculations is crucial for making informed financial decisions. For example, if a product is discounted by 20%, calculating the final price involves understanding percentages.
3. Data Analysis and Interpretation
In data analysis and interpretation, percentages are widely used to present data in a clear and concise manner. For example, expressing survey results as percentages helps visualize the proportion of respondents who hold specific opinions or preferences. This simplifies the understanding of complex datasets and allows for drawing meaningful conclusions.
4. Everyday Life
Percentages appear frequently in everyday life, from calculating tips in restaurants to understanding sales tax rates, evaluating discounts, interpreting nutritional information on food labels, and analyzing sports statistics. A solid grasp of percentages makes it easier to manage daily finances, make better consumer choices, and navigate various real-world situations.
Beyond the Basics: Advanced Percentage Calculations
While calculating 16 out of 20 as a percentage is relatively straightforward, more complex percentage problems can arise. These often involve finding the part, the whole, or the percentage itself when only two of these values are known.
Finding the Part
If you know the percentage and the whole, you can find the part using this formula:
(Percentage/100) * Whole = Part
For instance, if you need to find 25% of 200, the calculation would be:
(25/100) * 200 = 50
Finding the Whole
If you know the percentage and the part, you can find the whole using this formula:
(Part / Percentage) * 100 = Whole
For example, if 20 is 40% of a number, you would calculate the whole as follows:
(20 / 40) * 100 = 50
Percentage Increase and Decrease
Calculating percentage increase and decrease is another common application. The formulas for these are:
- Percentage Increase: [(New Value - Old Value) / Old Value] * 100%
- Percentage Decrease: [(Old Value - New Value) / Old Value] * 100%
These formulas are crucial for analyzing changes over time, such as population growth, price fluctuations, and economic indicators.
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: Consistent practice is key to mastering percentage calculations. Work through various examples and problems to build confidence and familiarity with different methods.
- Understand the Concepts: Don't just memorize formulas; understand the underlying concepts of percentages and fractions. This deeper understanding will make it easier to approach diverse percentage problems.
- Use Online Resources: There are many online resources, including calculators, tutorials, and practice exercises, that can assist in learning and reinforcing percentage calculation skills.
- Break Down Complex Problems: For more complex problems, break them down into smaller, manageable steps. This makes the overall task less daunting and reduces the likelihood of errors.
- Check Your Work: Always double-check your answers to ensure accuracy. Use different methods to solve the same problem, if possible, to verify your results.
Conclusion: The Significance of Percentage Calculations
The ability to calculate percentages is a valuable skill with wide-ranging applications in various fields. Understanding how to convert fractions to percentages and vice-versa allows for clearer data representation, effective problem-solving, and informed decision-making. By mastering percentage calculations and utilizing the various methods and tips discussed in this guide, you'll be well-equipped to handle a wide range of percentage-related challenges in both academic and professional settings, as well as in your everyday life. Remember that consistent practice and a solid understanding of the underlying concepts are crucial for achieving proficiency in this essential mathematical skill.
Latest Posts
Latest Posts
-
How Many 12 Oz Cups In A Gallon
Jul 12, 2025
-
How Much Older Is John The Baptist Than Jesus
Jul 12, 2025
-
How Many Teaspoons In A Pound Of Sugar
Jul 12, 2025
-
How Do You Pass Level 12 On Bloxorz
Jul 12, 2025
-
How Far Is 0 4 Miles To Walk
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 16 Out Of 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.