What Is 18/30 As A Percentage
Kalali
Apr 14, 2025 · 5 min read
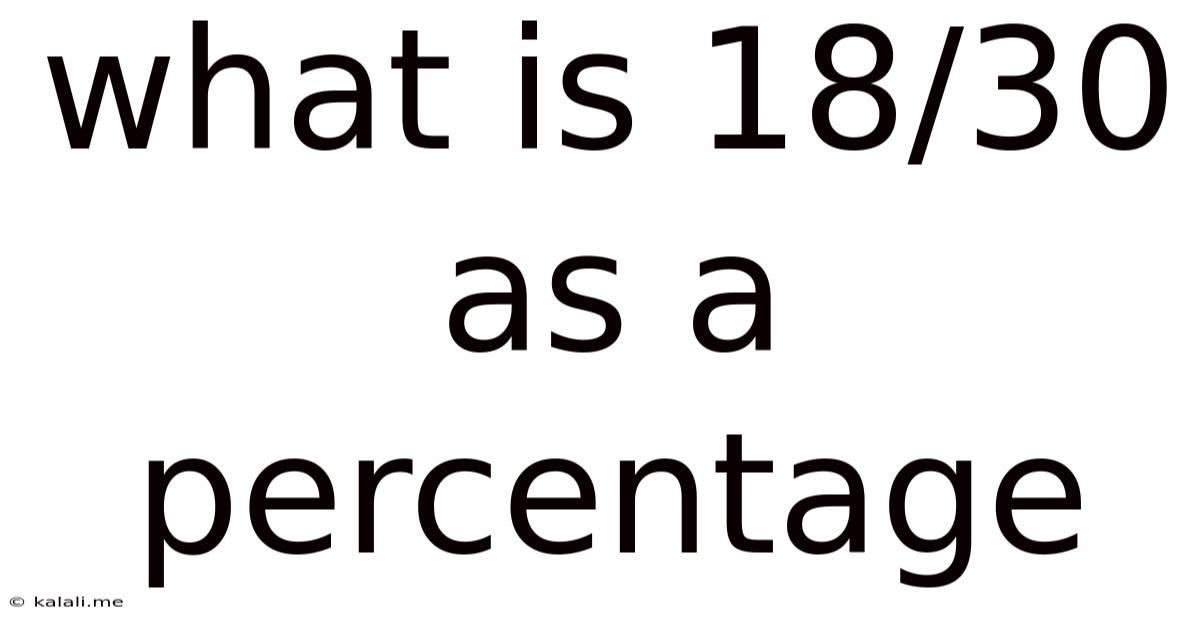
Table of Contents
What is 18/30 as a Percentage? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, applicable across various fields from finance and statistics to everyday life. This comprehensive guide will delve into the conversion of the fraction 18/30 into a percentage, explaining the process step-by-step and exploring related concepts. We'll cover multiple methods, ensuring you grasp the underlying principles and can confidently tackle similar conversions in the future. This guide also covers percentage increase and decrease calculations and explores real-world applications of percentage calculations.
Meta Description: Learn how to convert the fraction 18/30 into a percentage. This comprehensive guide provides multiple methods, explains the underlying concepts, and explores real-world applications. Master fraction-to-percentage conversion with ease!
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly revisit the concepts of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, 18/30 means 18 parts out of a total of 30 parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion relative to a whole, where the whole is considered to be 100%. For instance, 50% means 50 out of 100, or half.
Method 1: Simplifying the Fraction Before Conversion
The most efficient approach often involves simplifying the fraction before converting it to a percentage. This makes the calculation significantly easier.
-
Find the Greatest Common Divisor (GCD): The GCD of 18 and 30 is 6. This means both numbers are divisible by 6 without leaving a remainder.
-
Simplify the Fraction: Divide both the numerator and the denominator by the GCD:
18 ÷ 6 = 3 30 ÷ 6 = 5
This simplifies the fraction to 3/5.
-
Convert the Simplified Fraction to a Percentage: To convert a fraction to a percentage, multiply the fraction by 100%:
(3/5) * 100% = 60%
Therefore, 18/30 is equivalent to 60%.
Method 2: Direct Conversion without Simplification
While simplifying is generally recommended, you can directly convert 18/30 to a percentage without simplification.
-
Convert the Fraction to a Decimal: Divide the numerator (18) by the denominator (30):
18 ÷ 30 = 0.6
-
Convert the Decimal to a Percentage: Multiply the decimal by 100%:
0.6 * 100% = 60%
This method yields the same result: 18/30 equals 60%.
Method 3: Using Proportions
This method uses the concept of proportions to solve for the percentage.
We can set up a proportion:
18/30 = x/100
Where 'x' represents the percentage we want to find.
To solve for x, cross-multiply:
30x = 18 * 100 30x = 1800 x = 1800 ÷ 30 x = 60
Therefore, 18/30 is equivalent to 60%.
Understanding Percentage Increase and Decrease
Converting fractions to percentages is crucial when dealing with percentage increases or decreases. Let's say you initially had 30 items, and now you have 18. This represents a decrease. To calculate the percentage decrease:
-
Find the difference: 30 - 18 = 12
-
Divide the difference by the original amount: 12 ÷ 30 = 0.4
-
Multiply by 100%: 0.4 * 100% = 40%
Therefore, there's been a 40% decrease from 30 items to 18 items.
Conversely, if you started with 18 items and increased to 30, the percentage increase would be calculated as follows:
-
Find the difference: 30 - 18 = 12
-
Divide the difference by the original amount: 12 ÷ 18 = 0.666... (approximately)
-
Multiply by 100%: 0.666... * 100% ≈ 66.7%
Therefore, there's been an approximate 66.7% increase from 18 items to 30 items.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life:
- Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns.
- Retail: Determining sale prices, markups, and discounts.
- Statistics: Representing data in graphs and charts, analyzing survey results, and calculating probabilities.
- Science: Expressing concentrations of solutions, calculating experimental yields, and representing data in scientific reports.
- Everyday Life: Calculating tips, splitting bills, understanding nutrition labels, and interpreting statistical information in news reports.
Beyond the Basics: Working with More Complex Fractions
While 18/30 is a relatively straightforward example, the principles discussed apply to more complex fractions as well. For instance, converting a fraction like 27/63 to a percentage involves the same steps: simplify the fraction (both are divisible by 9, resulting in 3/7), convert the simplified fraction to a decimal (3 ÷ 7 ≈ 0.4286), and then multiply by 100% (approximately 42.86%).
Remember, the key is to understand the underlying principles of fractions, decimals, and percentages, and to choose the most efficient method for conversion, depending on the complexity of the fraction. Practicing with different examples will solidify your understanding and build confidence in tackling percentage calculations in any context.
Troubleshooting Common Mistakes
- Incorrect simplification: Ensure you find the greatest common divisor (GCD) to simplify the fraction correctly. Using a smaller common divisor will lead to an incorrect result.
- Division errors: Double-check your calculations when dividing the numerator by the denominator, particularly when dealing with decimals.
- Misunderstanding of percentage increase/decrease: Remember to always divide the difference by the original value when calculating percentage increases or decreases.
By understanding these principles and practicing regularly, you'll become proficient in converting fractions to percentages and applying this skill in various real-world scenarios. This knowledge empowers you to interpret data, make informed decisions, and navigate the numerical aspects of many facets of life with greater confidence and accuracy.
Latest Posts
Latest Posts
-
How Tall Is 20 Inches In Feet
Apr 16, 2025
-
Is Popping Popcorn A Chemical Change
Apr 16, 2025
-
How Many Electrons Does Uranium Have
Apr 16, 2025
-
What Term Refers To The Practice Of Renewing Destroyed Ecosystems
Apr 16, 2025
-
A Trapezoid Always Has Two Congruent Sides
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 18/30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.