What Is 2 3 Cup Times 2
Kalali
Jul 22, 2025 · 5 min read
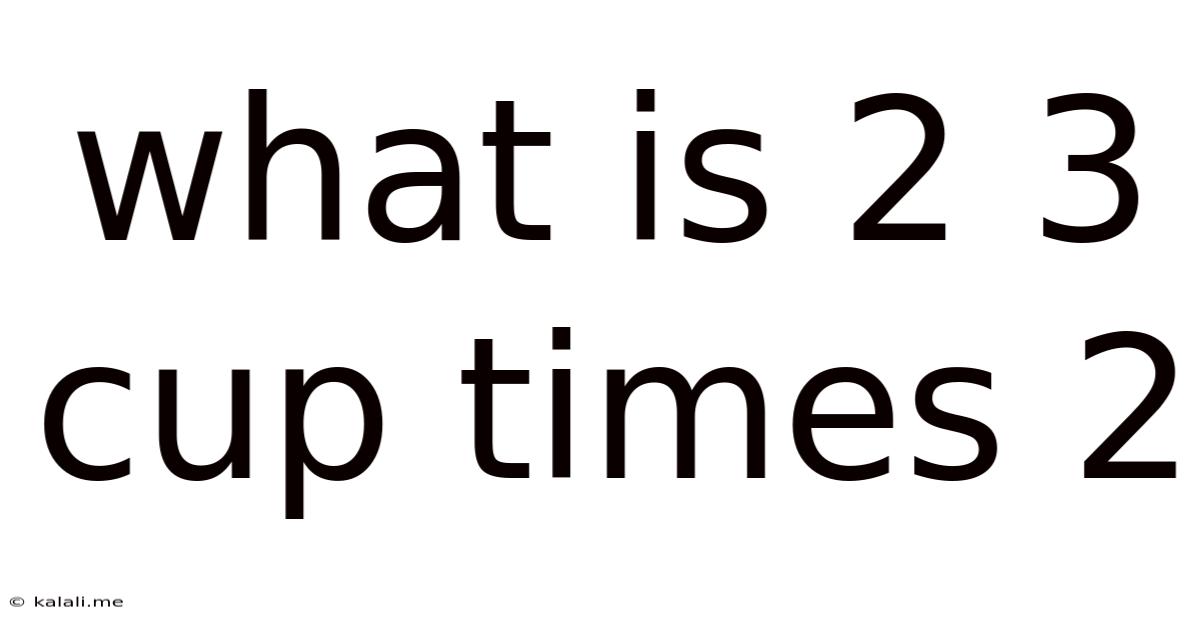
Table of Contents
Decoding "2 3/4 Cups Times 2": A Comprehensive Guide to Fraction Multiplication and Culinary Applications
This seemingly simple question, "What is 2 3/4 cups times 2?", opens the door to a surprisingly deep dive into the world of fractions, their practical applications, particularly in cooking and baking, and the importance of precise measurements in culinary creations. This article will not only answer the question directly but also explore the underlying mathematical concepts and provide you with a toolkit to confidently tackle similar problems in various contexts.
Meta Description: Learn how to multiply mixed numbers like 2 3/4 cups by 2. This comprehensive guide explains the math, provides real-world examples, especially in baking and cooking, and offers tips for accurate measurements in the kitchen.
Understanding the Problem: Mixed Numbers and Multiplication
The core of the problem lies in understanding mixed numbers. A mixed number, like 2 3/4, combines a whole number (2) and a fraction (3/4). To multiply this by 2, we need a systematic approach that ensures accuracy. We'll explore two common methods: converting to an improper fraction and the distributive method.
Method 1: Converting to an Improper Fraction
This method involves transforming the mixed number into an improper fraction – a fraction where the numerator is larger than the denominator.
-
Convert the Mixed Number: To convert 2 3/4 to an improper fraction, we multiply the whole number (2) by the denominator (4), add the numerator (3), and keep the same denominator (4). This gives us (2*4 + 3)/4 = 11/4.
-
Multiply the Fractions: Now, we multiply the improper fraction by 2: (11/4) * 2/1 = 22/4.
-
Simplify the Fraction: The resulting fraction, 22/4, can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2. This simplifies to 11/2.
-
Convert to a Mixed Number (Optional): Finally, we can convert the improper fraction 11/2 back to a mixed number. We divide the numerator (11) by the denominator (2). The quotient (5) becomes the whole number, and the remainder (1) becomes the numerator of the fraction, keeping the same denominator (2). This gives us the final answer: 5 1/2 cups.
Method 2: The Distributive Property
This method applies the distributive property of multiplication, which states that a(b + c) = ab + ac. We can use this to multiply each part of the mixed number separately.
-
Separate the Whole Number and Fraction: We separate 2 3/4 into its whole number part (2) and its fractional part (3/4).
-
Multiply Individually: We multiply each part by 2: 2 * 2 = 4 and (3/4) * 2 = 6/4.
-
Simplify and Combine: We simplify 6/4 to 3/2 or 1 1/2. Then, we add the results: 4 + 1 1/2 = 5 1/2 cups.
Why Precision Matters: Baking vs. Cooking
While both methods yield the same correct answer (5 1/2 cups), the importance of precision varies depending on the culinary context.
-
Baking: Baking is a precise science. Minor variations in ingredient measurements can significantly impact the final product's texture, taste, and overall success. Accurate measurements, using tools like measuring cups and kitchen scales, are crucial for achieving desired results. In a recipe calling for 2 3/4 cups of flour, using 5 1/2 cups would drastically alter the outcome.
-
Cooking: Cooking generally allows for more flexibility. While precise measurements are still important, slight deviations are often less critical than in baking. A recipe calling for 2 3/4 cups of broth might still taste delicious with a slightly different amount.
Real-World Applications: Recipes and Beyond
The ability to multiply fractions and mixed numbers is fundamental in many everyday situations, extending far beyond the kitchen. Consider these examples:
-
Scaling Recipes: Many recipes can be easily scaled up or down by multiplying or dividing ingredient amounts. If a recipe calls for 2 3/4 cups of sugar and you want to double the recipe, you'll need 5 1/2 cups.
-
Calculating Material Needs: Whether you're building a bookshelf, sewing a garment, or mixing paint, accurate measurements are crucial. Multiplying fractional amounts is often necessary to determine the total quantity of materials needed.
-
Understanding Unit Costs: When comparing prices of different-sized packages, understanding fractions helps calculate the unit cost (price per unit) to determine the best value.
Beyond the Basics: Working with More Complex Fractions
The principles discussed here can be extended to more complex scenarios involving multiple fractions and mixed numbers. Here are some examples and tips for handling them:
-
Multiplying Multiple Fractions: To multiply multiple fractions, simply multiply the numerators together and the denominators together. Remember to simplify the resulting fraction. For example, (1/2) * (3/4) * (2/3) = 6/24 = 1/4.
-
Multiplying Mixed Numbers by Other Mixed Numbers: Convert all mixed numbers to improper fractions before multiplying. Then, follow the standard fraction multiplication process.
-
Multiplying Fractions by Whole Numbers: Treat the whole number as a fraction with a denominator of 1. For example, 3 * (1/2) = 3/1 * 1/2 = 3/2 = 1 1/2.
-
Dividing Fractions: Remember that dividing by a fraction is the same as multiplying by its reciprocal (flip the numerator and denominator). For example, (1/2) ÷ (1/4) = (1/2) * (4/1) = 4/2 = 2.
Mastering Fraction Arithmetic: A Skill for Life
The ability to confidently work with fractions, including mixed numbers, is a valuable life skill. Whether you're a passionate baker, a DIY enthusiast, or simply someone who enjoys tackling mathematical problems, understanding these concepts opens doors to greater precision, accuracy, and problem-solving abilities. The simple question of "What is 2 3/4 cups times 2?" serves as a gateway to a broader understanding of fractions and their practical significance in everyday life. By mastering these fundamental arithmetic skills, you equip yourself to handle more complex calculations and confidently tackle various challenges with accuracy and precision. So next time you face a fractional equation, remember the techniques outlined above, and approach the problem with the confidence of a culinary mathematician!
Latest Posts
Latest Posts
-
Is It Illegal To Eat Oranges In The Bathtub
Jul 22, 2025
-
How Many Tablespoons Is 3 4 Oz Of Pudding Mix
Jul 22, 2025
-
How Much Does A 5 Gallon Paint Bucket Weigh
Jul 22, 2025
-
What Happened To Jp In Hells Kitchen
Jul 22, 2025
-
How Much Is Half A Ton In Pounds
Jul 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Cup Times 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.