What Is 2 3 Of 100
Kalali
Apr 05, 2025 · 5 min read
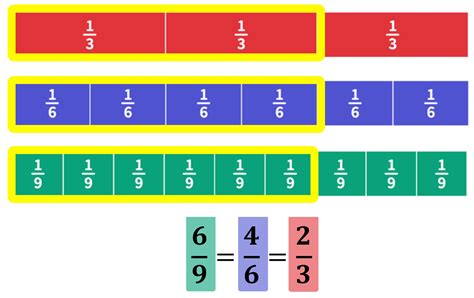
Table of Contents
What is 2/3 of 100? A Comprehensive Guide to Fractions and Percentages
Understanding fractions and percentages is fundamental to various aspects of life, from calculating discounts and tips to comprehending data in reports and presentations. This comprehensive guide will not only answer the question, "What is 2/3 of 100?" but also delve into the underlying concepts, providing you with a solid foundation in fractional arithmetic and percentage calculations. We’ll explore multiple methods for solving this problem and provide you with practical applications to solidify your understanding.
Understanding the Problem: 2/3 of 100
The question, "What is 2/3 of 100?", asks us to find two-thirds of the number 100. In simpler terms, we need to determine what portion of 100 represents two out of three equal parts. This seemingly simple question opens the door to exploring several mathematical concepts and techniques.
Method 1: Converting the Fraction to a Decimal
One straightforward approach involves converting the fraction 2/3 into its decimal equivalent. To do this, we divide the numerator (2) by the denominator (3):
2 ÷ 3 ≈ 0.6667 (rounded to four decimal places)
Now, we multiply this decimal by 100:
0.6667 * 100 ≈ 66.67
Therefore, 2/3 of 100 is approximately 66.67. It's important to note that the decimal representation of 2/3 is a repeating decimal (0.666...), meaning it goes on infinitely. We've rounded it for practicality.
Method 2: Finding One-Third and Doubling
Alternatively, we can find one-third of 100 first and then double the result to obtain two-thirds.
To find one-third of 100, we divide 100 by 3:
100 ÷ 3 ≈ 33.33 (rounded to two decimal places)
Now, we double this value to find two-thirds:
33.33 * 2 ≈ 66.66
This method yields a slightly different result due to rounding, but it demonstrates an alternative approach that can be useful for other fractional calculations.
Method 3: Using Proportions
Proportions offer a powerful way to solve this type of problem. We can set up a proportion:
2/3 = x/100
Where 'x' represents the value we're trying to find (2/3 of 100). To solve for 'x', we cross-multiply:
3x = 2 * 100
3x = 200
x = 200 ÷ 3
x ≈ 66.67
Understanding the Remainder
Notice that in all methods, we obtain a result with a decimal component. This is because 100 is not evenly divisible by 3. There's always a remainder. In the division 100 ÷ 3, the quotient is 33 and the remainder is 1. This remainder represents the portion of 100 that isn't perfectly divided into three equal parts.
Applying Fractions and Percentages in Real-World Scenarios
The ability to calculate fractions and percentages is crucial in various real-world situations:
1. Shopping Discounts:
Imagine a store offers a 2/3 discount on an item priced at $100. Using the methods above, you'd quickly determine the discount amount is approximately $66.67, and the final price would be $33.33 ($100 - $66.67).
2. Tip Calculations:
Restaurants often suggest tipping 15% or 20% of the bill. Calculating these percentages involves understanding the relationship between fractions and percentages. For example, a 15% tip on a $100 meal is the same as 3/20 (or 0.15) of $100, equaling $15.
3. Data Analysis:
In reports and presentations, data is often represented as percentages or fractions. The ability to understand and interpret these representations is key to grasping the information conveyed. For example, if a survey shows that 2/5 of respondents prefer a certain product, you would be able to quickly translate this to a percentage (40%).
4. Recipe Scaling:
When cooking, adjusting recipes requires understanding fractions. If a recipe calls for 2/3 cup of flour, and you want to double the recipe, you'll need to calculate 2 * (2/3) = 4/3 cups of flour, which is equal to 1 and 1/3 cups.
Expanding on Fractional Arithmetic
Beyond this specific problem, understanding fractions involves several key concepts:
-
Numerator and Denominator: The top number in a fraction (e.g., 2 in 2/3) is the numerator, representing the part. The bottom number (e.g., 3 in 2/3) is the denominator, representing the whole.
-
Equivalent Fractions: Different fractions can represent the same value. For example, 2/3, 4/6, and 6/9 are all equivalent fractions. Simplifying fractions to their lowest terms involves dividing both the numerator and the denominator by their greatest common divisor.
-
Adding and Subtracting Fractions: When adding or subtracting fractions, ensure they have a common denominator. For example, adding 1/2 and 1/3 requires finding a common denominator (6), resulting in (3/6) + (2/6) = 5/6.
-
Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators and multiplying the denominators. Dividing fractions involves inverting the second fraction and then multiplying.
Mastering Percentages
Percentages are essentially fractions with a denominator of 100. To convert a fraction to a percentage, multiply the fraction by 100%. For example, 2/3 * 100% ≈ 66.67%. To convert a percentage to a fraction, divide the percentage by 100 and simplify. For example, 66.67% = 66.67/100 ≈ 2/3.
Conclusion: Beyond the Calculation
While the answer to "What is 2/3 of 100?" is approximately 66.67, the true value lies in understanding the underlying principles of fractions and percentages. This knowledge empowers you to confidently tackle various mathematical challenges in everyday life, from managing finances to interpreting data and solving complex problems. Mastering these fundamental concepts is a crucial step in building a strong foundation in mathematics and its practical applications. By understanding the various methods for solving fractional problems, you can approach similar calculations with confidence and precision. Remember that even seemingly simple questions can lead to deeper understanding and valuable problem-solving skills.
Latest Posts
Latest Posts
-
11 Feet Is How Many Meters
Apr 06, 2025
-
How Long Is 9 Centimeters In Inches
Apr 06, 2025
-
How Many Seconds Are In 2 Minutes
Apr 06, 2025
-
What Percentage Of 20 Is 8
Apr 06, 2025
-
How Many Meters Are In 20 Yards
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
