What Is 2 3 Of 40
Kalali
Apr 27, 2025 · 4 min read
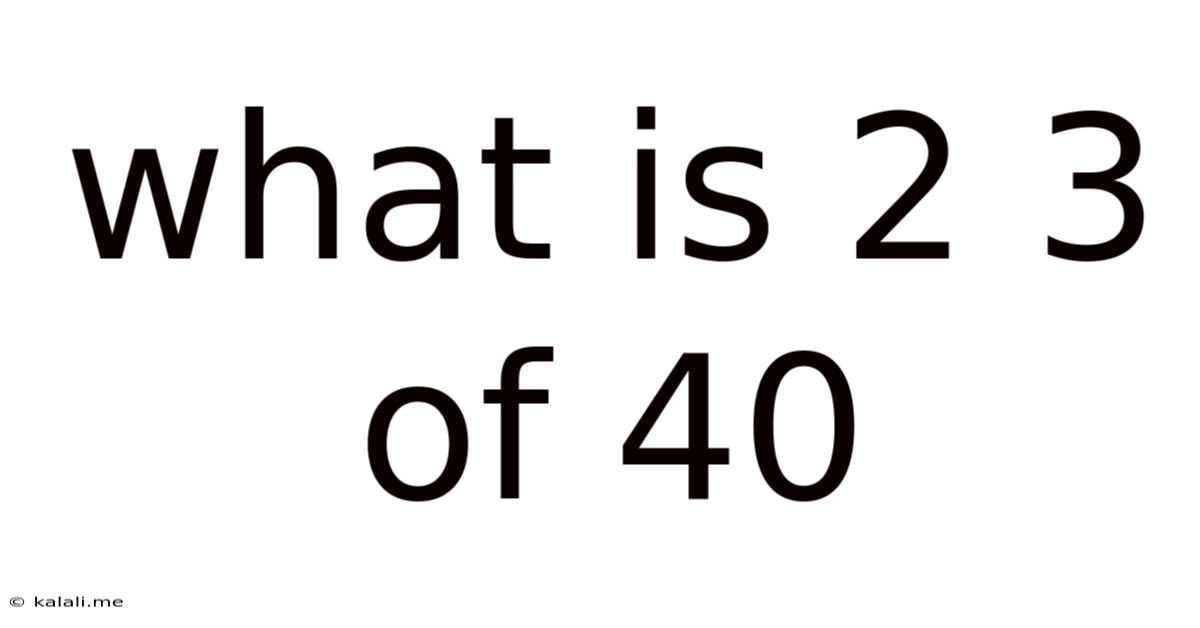
Table of Contents
What is 2/3 of 40? A Comprehensive Guide to Fractions and Their Applications
This seemingly simple question, "What is 2/3 of 40?", opens a door to a broader understanding of fractions, their practical applications, and how to confidently tackle similar problems. This article will delve into the solution, exploring various methods for calculating fractions of numbers, the underlying mathematical principles, and real-world examples demonstrating the relevance of this fundamental concept. Understanding this seemingly basic calculation is key to mastering more complex mathematical concepts.
Understanding Fractions: A Quick Refresher
Before diving into the calculation, let's briefly review the components of a fraction. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number, indicating the number of parts considered.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our problem, 2/3, '2' is the numerator and '3' is the denominator. This means we are considering 2 out of 3 equal parts.
Method 1: Direct Calculation
The most straightforward method to find 2/3 of 40 involves multiplying the fraction by the whole number:
(2/3) * 40
To perform this multiplication, we can rewrite 40 as a fraction (40/1):
(2/3) * (40/1) = (2 * 40) / (3 * 1) = 80/3
This gives us an improper fraction, meaning the numerator is larger than the denominator. To convert this to a mixed number (a whole number and a fraction), we divide 80 by 3:
80 ÷ 3 = 26 with a remainder of 2
Therefore, 80/3 is equal to 26 2/3.
So, 2/3 of 40 is 26 and 2/3.
Method 2: Finding One-Third, Then Doubling
Alternatively, we can break down the problem into smaller, more manageable steps. First, let's find one-third of 40:
40 ÷ 3 = 13.333... (approximately)
Since we want two-thirds, we simply double this result:
13.333... * 2 ≈ 26.666...
This again gives us approximately 26 and 2/3. Note that using decimals introduces a small degree of approximation. The fractional representation (26 2/3) is more precise.
Method 3: Using Decimal Equivalents
We can also convert the fraction 2/3 into its decimal equivalent:
2 ÷ 3 ≈ 0.666... (a recurring decimal)
Then, we multiply this decimal by 40:
0.666... * 40 ≈ 26.666...
This method, similar to the previous one, provides an approximate answer due to the recurring nature of the decimal. Again, the fractional form (26 2/3) is the more accurate representation.
Real-World Applications of Finding Fractions of Numbers
The ability to calculate fractions of numbers isn't just a theoretical exercise; it's a crucial skill with numerous practical applications in everyday life, including:
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. Understanding how to calculate fractions ensures you get the correct proportions. For example, if a recipe calls for 2/3 of a cup of flour, you'll need to know how to measure that accurately.
-
Shopping and Budgeting: Sales often advertise discounts as fractions (e.g., 1/3 off). Calculating the actual discount amount requires understanding how to find a fraction of the original price. Similarly, budgeting involves allocating portions of your income to different expenses, requiring fractional calculations.
-
Construction and Engineering: Precise measurements are vital in these fields, and fractions are frequently used. Calculating the amount of materials needed for a project often involves determining fractions of total requirements.
-
Data Analysis: In various fields, analyzing data often involves working with proportions and percentages, which are essentially fractions expressed in a different format.
-
Geometry and Measurement: Finding areas and volumes of shapes often requires fractional calculations. For example, determining the area of a triangle involves using the fraction 1/2 in the formula.
Beyond the Basics: Extending the Concept
Understanding "2/3 of 40" provides a solid foundation for tackling more complex fractional problems. These might involve:
- Mixed Numbers: Problems involving fractions and whole numbers combined.
- Improper Fractions: Fractions where the numerator is larger than the denominator.
- Multiple Fractions: Problems involving the multiplication or division of multiple fractions.
- Fractions with Variables: Introducing algebraic elements into fractional calculations.
Mastering these more advanced concepts requires a strong grasp of the fundamentals, starting with simple calculations like finding 2/3 of 40.
Conclusion: The Importance of Fractional Understanding
The seemingly simple problem, "What is 2/3 of 40?", serves as a gateway to understanding the broader world of fractions and their multifaceted applications. While the answer, 26 2/3, is readily calculable, the real value lies in comprehending the methods, principles, and practical implications involved. This understanding forms a cornerstone of mathematical literacy, crucial for navigating various aspects of daily life, academic pursuits, and professional endeavors. From scaling recipes to analyzing data, the ability to confidently work with fractions is an invaluable skill that extends far beyond the classroom. By mastering the fundamental concept demonstrated in this simple problem, one gains a significant advantage in tackling more complex mathematical challenges and confidently approaching real-world scenarios requiring fractional computations.
Latest Posts
Latest Posts
-
How Much Is 170 Cm In Inches
Apr 28, 2025
-
What Was Darwin Influences On Lyell And Hutton
Apr 28, 2025
-
Convert 99 Degrees Fahrenheit To Celsius
Apr 28, 2025
-
How Many Grams Is 25 Milligrams
Apr 28, 2025
-
X 2 X 2 3x 1
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.