What Is 2 5 8 In Decimals
Kalali
Apr 18, 2025 · 5 min read
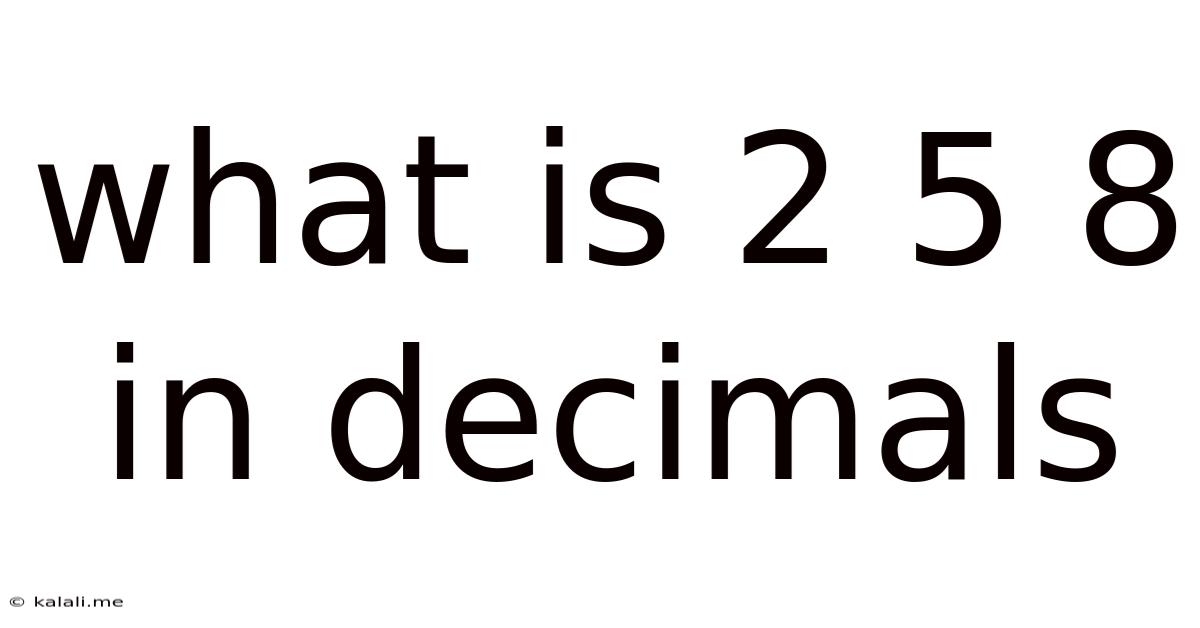
Table of Contents
Decoding 2 5 8: Understanding Mixed Numbers and Decimal Conversions
The seemingly simple question, "What is 2 5 8 in decimals?" actually opens the door to a broader understanding of number systems and the crucial process of converting between them. This article will thoroughly explore this conversion, explaining the underlying principles, offering multiple approaches to solving the problem, and providing additional context for readers seeking a deeper grasp of mathematical concepts. We'll delve into the mechanics of converting mixed numbers to improper fractions and then to decimals, highlighting common pitfalls and providing practical examples along the way. Understanding this process is fundamental for various applications, from everyday calculations to advanced mathematical problems.
Understanding the Components: Mixed Numbers and Decimals
Before we tackle the conversion of "2 5 8," let's first define the key terms involved.
-
Mixed Numbers: A mixed number combines a whole number and a proper fraction. In our example, "2 5 8" represents two whole units and five-eighths of another unit. The whole number is 2, and the fraction is 5/8.
-
Decimals: Decimals are another way of representing numbers, using a base-ten system. The digits to the right of the decimal point represent fractions with denominators that are powers of ten (10, 100, 1000, etc.). For instance, 0.5 represents 5/10, and 0.25 represents 25/100.
Our goal is to transform the mixed number 2 5/8 into its decimal equivalent. To achieve this, we'll follow a step-by-step process.
Method 1: Converting to an Improper Fraction, then to a Decimal
This is arguably the most common and straightforward method. It involves two distinct steps:
Step 1: Converting the Mixed Number to an Improper Fraction
A mixed number represents a whole number plus a fraction. To convert it into an improper fraction (where the numerator is larger than the denominator), we follow these steps:
- Multiply the whole number by the denominator of the fraction: 2 * 8 = 16
- Add the numerator of the fraction to the result: 16 + 5 = 21
- Keep the same denominator: The denominator remains 8.
Therefore, the mixed number 2 5/8 is equivalent to the improper fraction 21/8.
Step 2: Converting the Improper Fraction to a Decimal
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
21 ÷ 8 = 2.625
Therefore, 2 5/8 is equal to 2.625 in decimal form.
Method 2: Converting the Fraction Part to a Decimal, then Adding the Whole Number
This method breaks down the conversion into smaller, more manageable steps.
Step 1: Convert the Fractional Part to a Decimal
We focus solely on the fractional part of the mixed number: 5/8. We perform the division:
5 ÷ 8 = 0.625
Step 2: Add the Whole Number
Now, we simply add the whole number part of the mixed number (2) to the decimal value obtained in Step 1:
2 + 0.625 = 2.625
This method, while seemingly longer, can be more intuitive for some, allowing a clearer understanding of the individual components' contribution to the final decimal representation. It's particularly helpful for those who might find the improper fraction conversion step slightly more challenging.
Method 3: Utilizing Long Division (for a deeper understanding)
This method offers a more fundamental understanding of the conversion process, particularly beneficial for those seeking a deeper grasp of the underlying mathematical principles. While slightly more time-consuming, it reinforces the concept of division and its relationship to fractions and decimals.
To convert 2 5/8 to a decimal using long division, we first convert it to the improper fraction 21/8 as shown in Method 1. Then, we perform long division:
2.625
8 | 21.000
-16
50
-48
20
-16
40
-40
0
The long division shows that 21 divided by 8 equals 2.625, confirming our previous results. This method explicitly demonstrates the division process, enhancing comprehension for learners.
Addressing Potential Challenges and Common Errors
While the conversion process seems relatively straightforward, some common challenges can arise:
-
Incorrect Improper Fraction Conversion: A common mistake is incorrectly converting the mixed number to an improper fraction. Always double-check your multiplication and addition steps.
-
Division Errors: Accuracy in performing the division (either using a calculator or long division) is crucial. A slight error in the division will lead to an inaccurate decimal representation.
-
Understanding Terminating vs. Repeating Decimals: Not all fractions convert to terminating decimals (decimals that end). Some fractions result in repeating decimals (decimals with a sequence of digits that repeat infinitely). Understanding this distinction is important for interpreting results. For example, 1/3 converts to 0.333..., a repeating decimal. However, 5/8 (as in our example) converts to a terminating decimal.
Practical Applications and Further Exploration
The ability to convert mixed numbers to decimals is essential in various fields:
-
Engineering and Science: Many calculations in engineering and scientific fields require converting between fractions and decimals for precision and consistency.
-
Finance: Calculations involving percentages, interest rates, and financial ratios often involve converting fractions to decimals.
-
Everyday Calculations: Even in everyday life, understanding this conversion can be beneficial for tasks such as measuring ingredients in recipes, calculating discounts, or sharing items equally.
Beyond the basic conversion, further exploration could delve into:
-
Binary, Octal, and Hexadecimal Systems: Understanding how other number systems work helps put the decimal system into perspective.
-
Advanced Fraction Operations: Mastering more complex fraction operations, such as addition, subtraction, multiplication, and division of mixed numbers, further strengthens numerical skills.
-
Approximations and Rounding: Learning how to approximate decimal values and appropriately round them is crucial for practical applications where exact values might not be necessary.
In conclusion, the conversion of 2 5/8 to its decimal equivalent, 2.625, is a fundamental exercise illustrating the relationship between mixed numbers, improper fractions, and decimals. Mastering this conversion process is a cornerstone of numeracy and opens doors to understanding more complex mathematical concepts and their practical applications. By understanding the methods outlined above and addressing potential challenges, you can confidently navigate these conversions in various contexts.
Latest Posts
Latest Posts
-
How Many Parallel Sides Does A Square Have
Apr 19, 2025
-
What Is 62 Inches In Height
Apr 19, 2025
-
Least Common Multiple Of 7 And 10
Apr 19, 2025
-
How Many Cups In 16 9 Oz Of Water
Apr 19, 2025
-
Cuanto Es 60 Pulgadas En Metros
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 5 8 In Decimals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.