What Is 2.75 In A Fraction
Kalali
Apr 25, 2025 · 5 min read
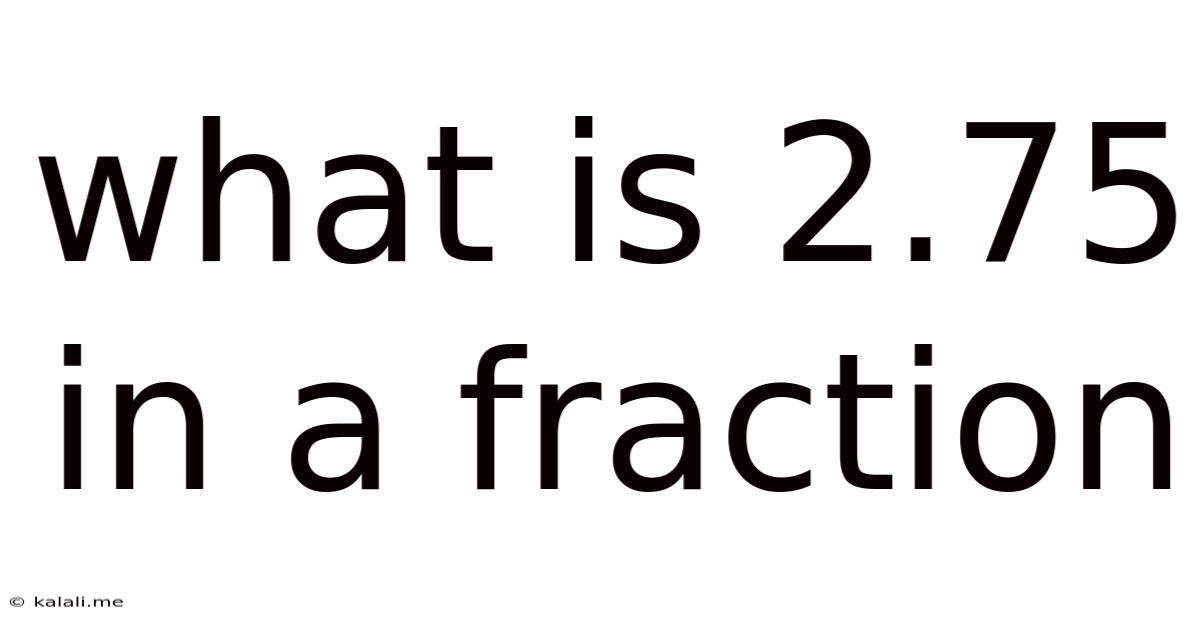
Table of Contents
What is 2.75 as a Fraction? A Comprehensive Guide
Understanding how to convert decimals to fractions is a fundamental skill in mathematics, with applications ranging from everyday calculations to advanced scientific work. This comprehensive guide will explore the conversion of the decimal 2.75 into a fraction, explaining the process step-by-step and offering insights into related concepts. We'll cover the method, explore different approaches, and discuss the significance of understanding decimal-to-fraction conversions. By the end, you'll not only know the fractional equivalent of 2.75 but also have a strong understanding of the underlying principles.
Meta Description: Learn how to convert the decimal 2.75 into a fraction. This detailed guide explains the process, offers alternative methods, and explores the importance of understanding decimal-to-fraction conversions in various mathematical contexts.
Understanding Decimals and Fractions
Before diving into the conversion, let's refresh our understanding of decimals and fractions.
-
Decimals: Decimals are a way of representing numbers that are not whole numbers. They use a base-ten system, where each digit to the right of the decimal point represents a power of ten (tenths, hundredths, thousandths, and so on). For example, 2.75 means 2 + 7/10 + 5/100.
-
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, 1/2 represents one out of two equal parts.
Converting 2.75 to a Fraction: The Step-by-Step Method
The most common method for converting a decimal to a fraction involves understanding the place value of the digits after the decimal point. In 2.75, the ".75" represents seventy-five hundredths. This can be written as a fraction directly:
-
Write the decimal part as a fraction: 0.75 can be written as 75/100.
-
Combine the whole number and the fraction: The whole number 2 remains as it is. So we have 2 + 75/100.
-
Simplify the fraction: The fraction 75/100 can be simplified by finding the greatest common divisor (GCD) of 75 and 100. The GCD of 75 and 100 is 25. Dividing both the numerator and the denominator by 25, we get 3/4.
-
Combine the whole number and the simplified fraction: This gives us the final answer: 2 + 3/4, which can also be written as the improper fraction 11/4 (by converting 2 to 8/4 and adding it to 3/4).
Therefore, 2.75 as a fraction is 11/4 or 2 3/4. Both representations are correct, with the mixed number (2 3/4) often being preferred for its readability.
Alternative Methods for Conversion
While the step-by-step method is straightforward, other methods can be used to convert decimals to fractions. Let's explore one alternative:
Using Powers of 10: This method involves writing the decimal as a fraction with a power of 10 as the denominator. For 2.75:
-
Write the decimal as a fraction with a power of 10: 2.75 can be written as 275/100.
-
Simplify the fraction: As before, we find the GCD of 275 and 100, which is 25. Simplifying, we get 11/4.
This method directly converts the entire decimal to a fraction and then simplifies, offering a slightly more concise approach.
Understanding the Importance of Decimal-to-Fraction Conversions
The ability to convert decimals to fractions is crucial for several reasons:
-
Mathematical Operations: Fractions are often easier to work with when performing certain mathematical operations, particularly addition, subtraction, multiplication, and division of unlike denominators, especially if you are dealing with fractions which cannot be easily simplified into decimals.
-
Precision: Fractions can represent exact values, unlike decimals, which sometimes involve approximations, especially irrational numbers. This accuracy is vital in fields like engineering and science. For instance, using 11/4 ensures precise calculations rather than relying on the decimal equivalent of 2.75, which might be truncated or rounded.
-
Real-World Applications: Many everyday situations involve fractions. Consider recipes (1/2 cup of sugar), measurements (3/4 inch), or sharing items (dividing a pizza into equal slices). The ability to convert between decimals and fractions allows for seamless transitions between these contexts.
-
Problem Solving: Converting decimals to fractions is often a necessary step in solving mathematical problems that involve both decimal and fractional values. The ability to switch easily between forms enhances problem-solving skills significantly.
Further Exploration: Converting Other Decimals to Fractions
The principles discussed above apply to converting any decimal to a fraction. Here are a few examples to solidify your understanding:
-
0.5: This is equivalent to 5/10, which simplifies to 1/2.
-
0.25: This is equivalent to 25/100, which simplifies to 1/4.
-
0.125: This is equivalent to 125/1000, which simplifies to 1/8.
-
3.75: This is equivalent to 3 + 75/100, which simplifies to 3 + 3/4 or 15/4.
By systematically applying the methods described earlier, you can confidently convert any decimal number into its equivalent fractional representation. Remember to always simplify the resulting fraction to its lowest terms for the most efficient and accurate representation.
Conclusion: Mastering Decimal-to-Fraction Conversions
Converting decimals to fractions is a fundamental skill that extends far beyond basic arithmetic. It's a crucial concept in various mathematical applications and real-world situations. Understanding the processes, alternative methods, and the underlying principles empowers you to confidently tackle decimal-to-fraction conversions and further enhances your mathematical proficiency. Remember to practice regularly to solidify your understanding and improve your speed and accuracy in solving problems that involve both decimals and fractions. Through consistent practice and a solid understanding of the underlying principles, mastering this skill will significantly benefit your mathematical journey.
Latest Posts
Latest Posts
-
1 Percent Of 1 Million Dollars
Apr 25, 2025
-
Inverse Of 1 To 1 Function
Apr 25, 2025
-
35 Is What Percent Of 100
Apr 25, 2025
-
1 Gallon Is How Many Ml
Apr 25, 2025
-
How Do You Divide Fractions With Negative Numbers
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 2.75 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.