What Is 2 Percent Of 25
Kalali
Apr 16, 2025 · 6 min read
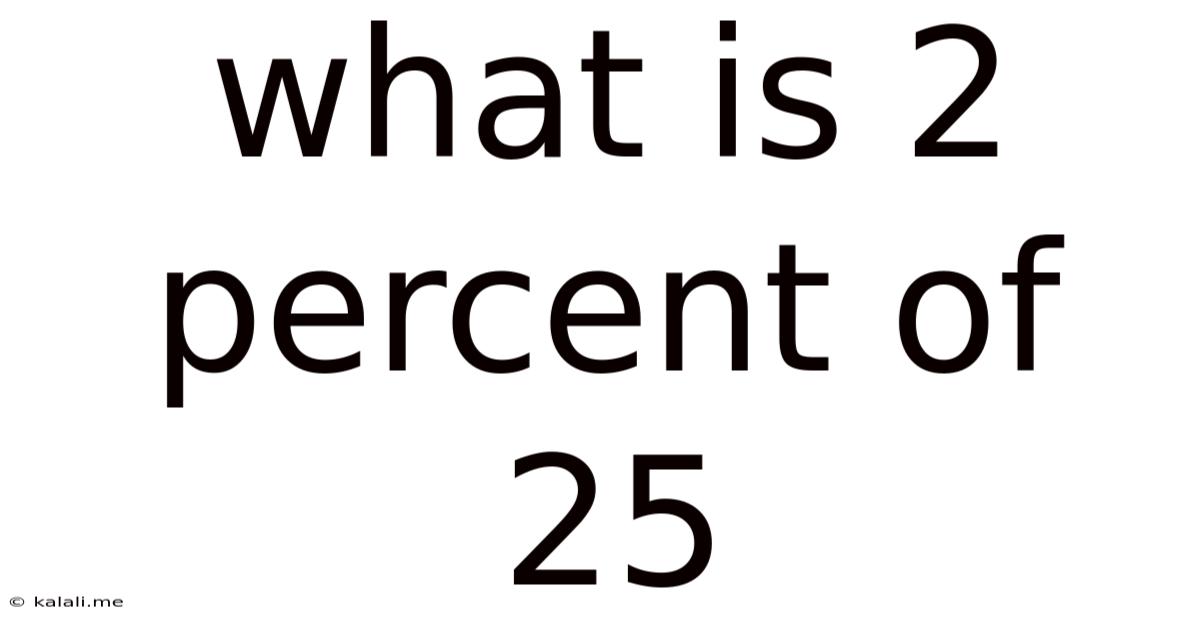
Table of Contents
What is 2 Percent of 25? A Deep Dive into Percentages and Their Applications
Meta Description: Uncover the simple calculation of 2% of 25 and explore the broader world of percentages, including practical applications, different calculation methods, and real-world examples. This comprehensive guide will equip you with the knowledge to confidently tackle percentage problems.
Finding 2 percent of 25 might seem like a trivial task, a simple calculation easily solved with a calculator. However, understanding the underlying principles of percentages and their diverse applications extends far beyond this basic arithmetic. This article delves into the calculation itself, explores the various methods for solving percentage problems, and illuminates the significant role percentages play in numerous aspects of daily life, from finance and shopping to statistics and scientific analysis.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "per hundred." Therefore, 2% can be understood as 2 out of every 100, or 2/100. This fraction can be simplified to 1/50. This fundamental understanding forms the bedrock for all percentage calculations.
Calculating 2% of 25: Three Approaches
There are several ways to calculate 2% of 25. Let's explore three common methods:
1. The Fractional Method:
This method leverages the fractional representation of a percentage. As mentioned earlier, 2% is equivalent to 2/100 or 1/50. To find 2% of 25, we simply multiply 25 by the fraction 2/100:
25 x (2/100) = 0.5
Therefore, 2% of 25 is 0.5 or one-half.
2. The Decimal Method:
This method involves converting the percentage into a decimal. To convert a percentage to a decimal, simply divide the percentage by 100. In this case, 2% becomes 0.02 (2 divided by 100). Then, multiply this decimal by the number you're finding the percentage of:
25 x 0.02 = 0.5
This method yields the same result as the fractional method: 0.5.
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value. We can represent the problem as:
2/100 = x/25
To solve for x (which represents 2% of 25), we cross-multiply:
100x = 2 x 25 100x = 50 x = 50/100 x = 0.5
Again, we arrive at the same answer: 0.5.
Beyond the Calculation: Real-World Applications of Percentages
While the calculation of 2% of 25 is straightforward, the concept of percentages permeates numerous facets of our lives. Understanding percentages is crucial for:
-
Financial Literacy: Percentages are fundamental to understanding interest rates on loans and savings accounts, calculating taxes, and comprehending investment returns. For example, a 5% interest rate on a savings account means your money grows by 5% annually. Similarly, understanding sales tax (often expressed as a percentage) helps you determine the final cost of a purchase. Analyzing financial statements often involves understanding percentage changes in revenue, profit margins, and expenses. Knowing percentage increases or decreases in your investments is critical for successful financial planning.
-
Shopping and Discounts: Retailers frequently advertise sales and discounts using percentages. "20% off" means you pay 80% of the original price. Being able to quickly calculate the discounted price helps you make informed purchasing decisions and compare offers effectively. This skill extends beyond simple discounts to more complex scenarios involving multiple discounts, coupons, and loyalty points. Understanding compound discounts can save significant amounts of money.
-
Statistics and Data Analysis: Percentages are invaluable for presenting and interpreting data. For example, survey results are frequently expressed as percentages to show the proportion of respondents who chose a particular option. Understanding percentage changes in various statistical data is critical in many fields, from epidemiology and public health to market research and political polling. Statistical significance is often expressed using percentages.
-
Scientific Research: Percentages are frequently used in scientific studies to represent proportions, error margins, and changes in experimental data. For instance, researchers might report a percentage increase in plant growth after applying a certain fertilizer, or a percentage decrease in disease incidence after a vaccination campaign. In many scientific fields, percentages are critical to making meaningful comparisons and evaluating the significance of research findings. Understanding percentages is crucial for correctly interpreting and applying scientific research.
-
Everyday Life: Even simple tasks such as calculating tips in a restaurant, determining the percentage of a task completed, or understanding nutritional information on food labels involve percentages. Understanding the proportion of ingredients in a recipe, the percentage of daily recommended intake of vitamins and minerals, or the percentage of daily water intake are all examples where knowledge of percentages becomes useful.
Advanced Percentage Calculations
Beyond the simple calculation of 2% of 25, more complex scenarios might require understanding:
-
Percentage Increase/Decrease: Calculating the percentage change between two numbers. For example, if a product's price increases from $20 to $25, the percentage increase is calculated as [(25-20)/20] x 100% = 25%. Similarly, understanding percentage decrease is equally important.
-
Finding the Original Value: If you know the percentage increase or decrease and the final value, you can work backward to find the original value.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding compound interest is vital for long-term financial planning.
-
Percentage Points: This is a crucial distinction; a percentage point refers to the difference between two percentages, not a percentage of the difference. For example, an increase from 20% to 22% is a 2 percentage point increase, not a 10% increase. This distinction is vital for clear communication and correct interpretation of statistical data.
Mastering Percentages: Practice and Resources
Mastering percentages requires practice. Start with simple calculations like the one discussed in this article and gradually work your way up to more complex problems. Numerous online resources, including educational websites and YouTube tutorials, offer interactive exercises and explanations to aid in your learning journey. Practicing regularly will build confidence and proficiency in solving various percentage problems.
Conclusion
While the question "What is 2 percent of 25?" might appear simplistic, it provides a gateway to understanding the broader significance of percentages in our daily lives. The ability to calculate percentages effectively is a crucial skill for various aspects of life, ranging from personal finance and shopping to scientific analysis and statistical interpretation. This article has provided multiple methods for calculating percentages and highlighted their vast and diverse applications. By understanding these concepts and practicing regularly, you can enhance your numerical literacy and confidently tackle a wide range of percentage-related problems. Remember, the seemingly simple calculation of 2% of 25 forms the foundation for a deeper understanding of a critical concept that empowers informed decision-making across numerous fields.
Latest Posts
Latest Posts
-
How Many Species Of Reptiles Are There
Apr 19, 2025
-
6 Cups Equals How Many Pints
Apr 19, 2025
-
How To Do Mole To Mass Conversions
Apr 19, 2025
-
Life Cycle Of A Plant Bean
Apr 19, 2025
-
How Do You Find The Mean In A Dot Plot
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.