What Is 2 To The Power Of 1
Kalali
Mar 05, 2025 · 6 min read
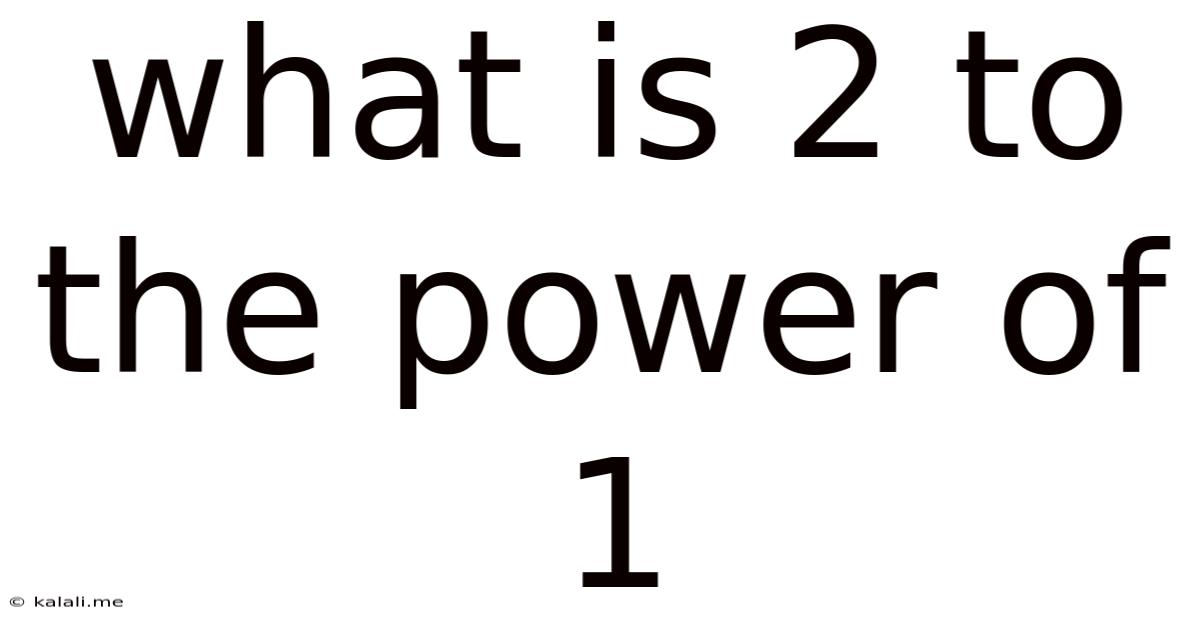
Table of Contents
What is 2 to the Power of 1? A Deep Dive into Exponentiation
The seemingly simple question, "What is 2 to the power of 1?" might appear trivial at first glance. However, understanding this fundamental concept unlocks a deeper appreciation of exponentiation, a crucial mathematical operation with far-reaching applications across numerous fields. This article will explore not just the answer but delve into the underlying principles of exponents, their properties, and their relevance in various contexts, going far beyond the immediate solution.
Understanding Exponentiation: Beyond the Basics
Exponentiation, often represented as b<sup>e</sup>, signifies repeated multiplication. Here, 'b' is the base, and 'e' is the exponent. The exponent indicates how many times the base is multiplied by itself. For instance, 2<sup>3</sup> (2 to the power of 3) means 2 × 2 × 2 = 8. The base (2) is multiplied by itself three (exponent) times.
The Case of 2<sup>1</sup>
Now, let's address our central question: What is 2<sup>1</sup>? Following the definition of exponentiation, it simply means 2 multiplied by itself one time. Therefore, 2<sup>1</sup> = 2. This might seem self-evident, but understanding this basic case is foundational to comprehending more complex exponential expressions.
Properties of Exponents: A Foundation for Understanding
The seemingly simple operation of exponentiation possesses several key properties that govern how we manipulate and solve exponential equations. Understanding these properties is crucial for working with exponents effectively.
Property 1: Exponent of Zero
Any non-zero number raised to the power of zero is equal to 1. This might seem counterintuitive, but it's consistent with the pattern of decreasing exponents. For example:
- 2<sup>3</sup> = 8
- 2<sup>2</sup> = 4
- 2<sup>1</sup> = 2
- 2<sup>0</sup> = 1
Observe how dividing by 2 with each decreasing exponent leads to the next value. This pattern logically leads to 2<sup>0</sup> equaling 1. Mathematically, this is defined as follows:
b<sup>0</sup> = 1, where b ≠ 0
Property 2: Exponent of One
This is the property directly related to our initial question. Any number raised to the power of one is simply equal to itself. This can be expressed as:
b<sup>1</sup> = b
Again, this is consistent with the definition of exponentiation. Multiplying any number by itself only once results in the original number itself.
Property 3: Product of Powers with the Same Base
When multiplying exponential expressions with the same base, we can add the exponents:
b<sup>m</sup> × b<sup>n</sup> = b<sup>(m+n)</sup>
For example, 2<sup>2</sup> × 2<sup>3</sup> = 2<sup>(2+3)</sup> = 2<sup>5</sup> = 32.
Property 4: Quotient of Powers with the Same Base
When dividing exponential expressions with the same base, we subtract the exponents:
b<sup>m</sup> ÷ b<sup>n</sup> = b<sup>(m-n)</sup>
For example, 2<sup>5</sup> ÷ 2<sup>2</sup> = 2<sup>(5-2)</sup> = 2<sup>3</sup> = 8.
Property 5: Power of a Power
When raising an exponential expression to another power, we multiply the exponents:
(b<sup>m</sup>)<sup>n</sup> = b<sup>(m×n)</sup>
For example, (2<sup>3</sup>)<sup>2</sup> = 2<sup>(3×2)</sup> = 2<sup>6</sup> = 64.
Applications of Exponentiation: Beyond the Classroom
The concept of exponentiation isn't confined to theoretical mathematics. It finds extensive practical applications in various fields:
1. Compound Interest: The Power of Growth
In finance, exponential functions are used to calculate compound interest. Compound interest earns interest not only on the principal amount but also on the accumulated interest. The formula for compound interest involves exponentiation:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
The exponential term (1 + r/n)^(nt) shows how the investment grows exponentially over time.
2. Population Growth: Modeling Exponential Increase
Exponential functions are also crucial in modeling population growth. Under ideal conditions, population growth can follow an exponential pattern. The larger the population, the faster it grows. This can be represented using a similar formula to compound interest, but with different parameters representing population growth rates.
3. Radioactive Decay: Modeling Exponential Decrease
In contrast to population growth, radioactive decay follows an exponential decay pattern. The rate of decay is proportional to the amount of radioactive material present. The remaining amount of the substance can be calculated using an exponential function, typically involving a negative exponent to represent the decrease over time.
4. Computer Science: Binary Numbers and Data Storage
In computer science, the binary number system uses only two digits (0 and 1). Each digit represents a power of 2. For example, the binary number 1011 is equivalent to (1 × 2<sup>3</sup>) + (0 × 2<sup>2</sup>) + (1 × 2<sup>1</sup>) + (1 × 2<sup>0</sup>) = 8 + 0 + 2 + 1 = 11 in decimal. Understanding exponents is fundamental to working with binary numbers and data storage.
5. Physics: Describing Exponential Phenomena
Many physical phenomena exhibit exponential behavior, including the decay of electrical charge in a capacitor, the cooling of objects according to Newton's Law of Cooling, and the spread of certain types of waves.
6. Biology: Modelling Biological Processes
Exponential growth and decay are also widely used to model biological processes such as bacterial growth, enzyme kinetics and drug metabolism within the body.
Expanding on the Concept: Higher Powers of 2
While our focus has been on 2<sup>1</sup>, exploring higher powers of 2 provides further insight into the nature of exponentiation. Let’s examine the progression:
- 2<sup>1</sup> = 2
- 2<sup>2</sup> = 4
- 2<sup>3</sup> = 8
- 2<sup>4</sup> = 16
- 2<sup>5</sup> = 32
- 2<sup>6</sup> = 64
- 2<sup>7</sup> = 128
- 2<sup>8</sup> = 256
- 2<sup>9</sup> = 512
- 2<sup>10</sup> = 1024
Notice the rapid increase in values. This illustrates the powerful nature of exponential growth, where small changes in the exponent lead to significant changes in the result. This rapid growth is a defining characteristic of exponential functions, contrasted with linear functions where the change is constant.
Conclusion: The Significance of Understanding Exponentiation
The answer to "What is 2 to the power of 1?" might seem simple, but it serves as a gateway to understanding the broader realm of exponentiation. This seemingly elementary concept underpins numerous mathematical principles and finds wide-ranging applications in various disciplines. From calculating compound interest to modeling population growth and understanding binary numbers, exponentiation is a crucial mathematical tool with far-reaching implications. A solid grasp of exponentiation and its properties is essential for anyone seeking to delve deeper into mathematics, science, finance, or computer science. The seemingly simple 2<sup>1</sup> = 2 is, therefore, a fundamental building block for more complex and significant calculations and models.
Latest Posts
Latest Posts
-
How Long Is A China Man Joke
Jul 05, 2025
-
What Episode Does Ichigo Get His Powers Back
Jul 05, 2025
-
Pokemon Mystery Dungeon Red Rescue Team Codes
Jul 05, 2025
-
How Much Is 25 20 Dollar Bills
Jul 05, 2025
-
How Many Apples In 3 Lb Bag
Jul 05, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 To The Power Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.