What Is 2 To The Power Of 6
Kalali
Mar 31, 2025 · 5 min read
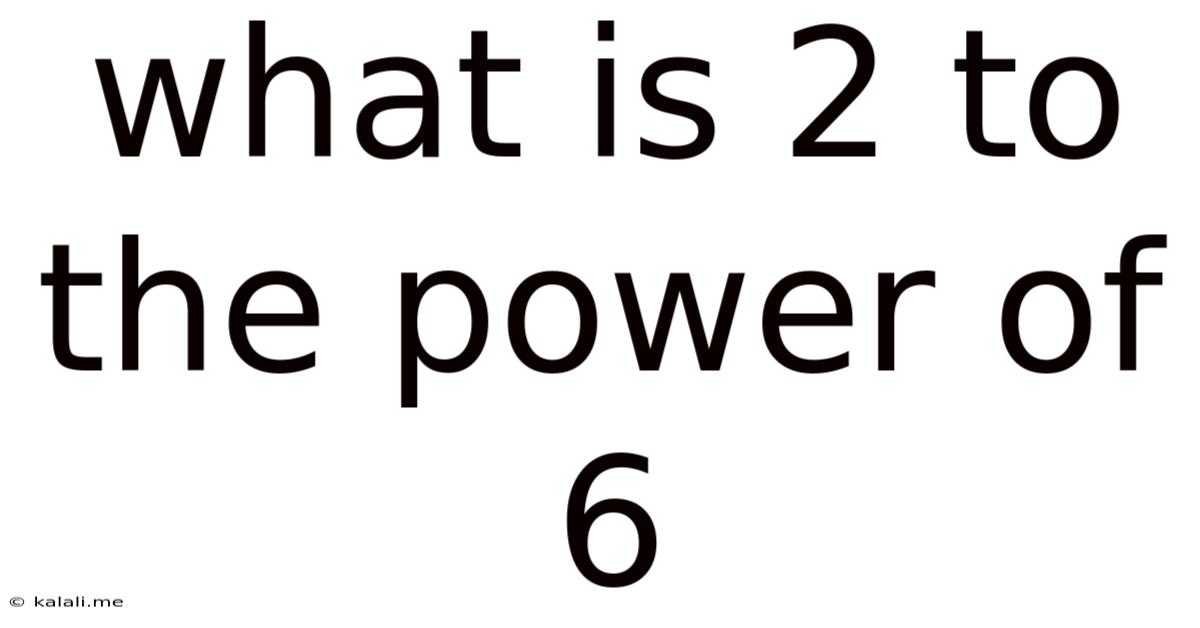
Table of Contents
What is 2 to the Power of 6? A Deep Dive into Exponentiation
The seemingly simple question, "What is 2 to the power of 6?" opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is straightforward – 64 – the journey to understanding how we arrive at this answer, and the broader implications of exponential growth, is far more enriching. This article will explore this seemingly simple calculation in detail, delving into the fundamental concepts, practical applications, and even some surprising connections to other areas of mathematics and science.
Understanding Exponentiation: The Basics
Exponentiation, at its core, represents repeated multiplication. The expression 2<sup>6</sup> means multiplying the base number (2) by itself six times. We can write this out explicitly as: 2 × 2 × 2 × 2 × 2 × 2. This process of repeated multiplication is crucial to understanding exponential growth and its widespread applications.
Key Terminology: Base and Exponent
Let's clarify the terminology:
- Base: The number being multiplied repeatedly (in this case, 2).
- Exponent: The number indicating how many times the base is multiplied by itself (in this case, 6). This is also often referred to as the power.
Understanding these terms is paramount to grasping exponentiation and related mathematical concepts.
Calculating 2 to the Power of 6: Step-by-Step
While a simple calculator can swiftly provide the answer, let's break down the calculation manually to reinforce the understanding of the process:
- 2 × 2 = 4: Our first multiplication step.
- 4 × 2 = 8: Multiplying the result by the base again.
- 8 × 2 = 16: Continuing the pattern.
- 16 × 2 = 32: Halfway there!
- 32 × 2 = 64: And finally, we arrive at our answer.
Therefore, 2<sup>6</sup> = 64.
Beyond the Calculation: The Significance of Exponential Growth
The seemingly simple calculation of 2<sup>6</sup> represents a fundamental concept in mathematics and science: exponential growth. This type of growth is characterized by an increasingly rapid rate of increase over time. Unlike linear growth, where the rate of increase is constant, exponential growth accelerates. This leads to dramatic changes, particularly over longer periods.
Real-World Examples of Exponential Growth
Exponential growth is observable in numerous real-world scenarios:
- Compound Interest: The interest earned on an investment is added to the principal amount, and subsequent interest is calculated on the larger sum. This compounding effect leads to exponential growth of the investment over time.
- Population Growth: Under ideal conditions, populations (of humans, bacteria, or other organisms) can exhibit exponential growth. Each individual produces offspring, who in turn produce offspring, leading to a rapidly expanding population.
- Viral Spread: The spread of viral infections often follows an exponential pattern. Each infected individual can infect multiple others, resulting in a geometric increase in the number of cases.
- Technological Advancement: The pace of technological innovation often exhibits exponential growth. New technologies build upon existing ones, accelerating the rate of progress.
Exponential Decay: The Flip Side
While exponential growth is prevalent, its counterpart, exponential decay, is equally important. Exponential decay describes the decrease in a quantity over time, where the rate of decrease is proportional to the current quantity. Examples include radioactive decay and the cooling of an object.
Mathematical Properties and Extensions
The concept of 2<sup>6</sup> extends far beyond a simple calculation. It connects to various mathematical properties and concepts:
Powers of 2 in Binary Numbers
The number 2 holds a special place in computer science due to the binary number system. Binary uses only two digits, 0 and 1, to represent all numbers. Powers of 2 are fundamental to understanding binary representation, as each position in a binary number corresponds to a power of 2 (e.g., 128, 64, 32, 16, 8, 4, 2, 1). Understanding 2<sup>6</sup> is thus essential for comprehending how numbers are represented and manipulated in computers.
Logarithms: The Inverse Operation
Logarithms are the inverse operation of exponentiation. If 2<sup>6</sup> = 64, then the logarithm base 2 of 64 is 6 (log₂64 = 6). Logarithms are crucial tools in various fields, including science, engineering, and finance, for solving exponential equations and analyzing data.
Combinatorics and Probability
Powers of 2 frequently appear in combinatorics and probability. For example, the number of subsets of a set with n elements is 2<sup>n</sup>. Understanding this connection reveals the power of exponentiation in counting problems and calculating probabilities.
Applications in Different Fields
The concept of 2<sup>6</sup> and exponential functions, in general, have far-reaching applications across a variety of fields:
Computer Science and Technology
As mentioned earlier, powers of 2 are fundamental to the binary system, impacting computer architecture, data storage, and network protocols. Understanding exponential growth is also crucial for analyzing algorithm efficiency and predicting system performance.
Biology and Medicine
Exponential growth models are used to study population dynamics, bacterial growth, and the spread of infectious diseases. This understanding is critical for predicting outbreaks, developing treatment strategies, and managing public health resources.
Finance and Economics
Exponential growth and decay models are essential in finance for understanding compound interest, investment growth, loan amortization, and the time value of money. Economic models often use exponential functions to describe economic growth and decay.
Physics and Engineering
Exponential functions describe many physical phenomena, including radioactive decay, the cooling of objects, and the attenuation of signals. Understanding these functions is crucial for designing and analyzing various engineering systems.
Conclusion: More Than Just a Calculation
The seemingly simple question, "What is 2 to the power of 6?" leads to a rich exploration of exponentiation, exponential growth and decay, and their far-reaching implications. From the binary number system to complex financial models and biological processes, understanding exponential functions is essential for comprehending the world around us. This exploration highlights the interconnectedness of mathematical concepts and their pervasive influence on various scientific and technological fields. The number 64, the result of 2<sup>6</sup>, therefore, represents more than just a calculation; it serves as a gateway to a vast and fascinating world of mathematical exploration. Further exploration into these topics will undoubtedly reveal even more intricate connections and applications, solidifying the importance of this seemingly basic mathematical concept.
Latest Posts
Latest Posts
-
How Many Cups Is 33 Oz
Apr 02, 2025
-
Cuanto Es 10 Millas En Kilometros
Apr 02, 2025
-
How Many Cm Is 71 Inches
Apr 02, 2025
-
How Tall Is 65inches In Feet
Apr 02, 2025
-
Least Common Multiple Of 5 And 9
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 To The Power Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
