What Is 20 Off Of 120
Kalali
Apr 09, 2025 · 5 min read
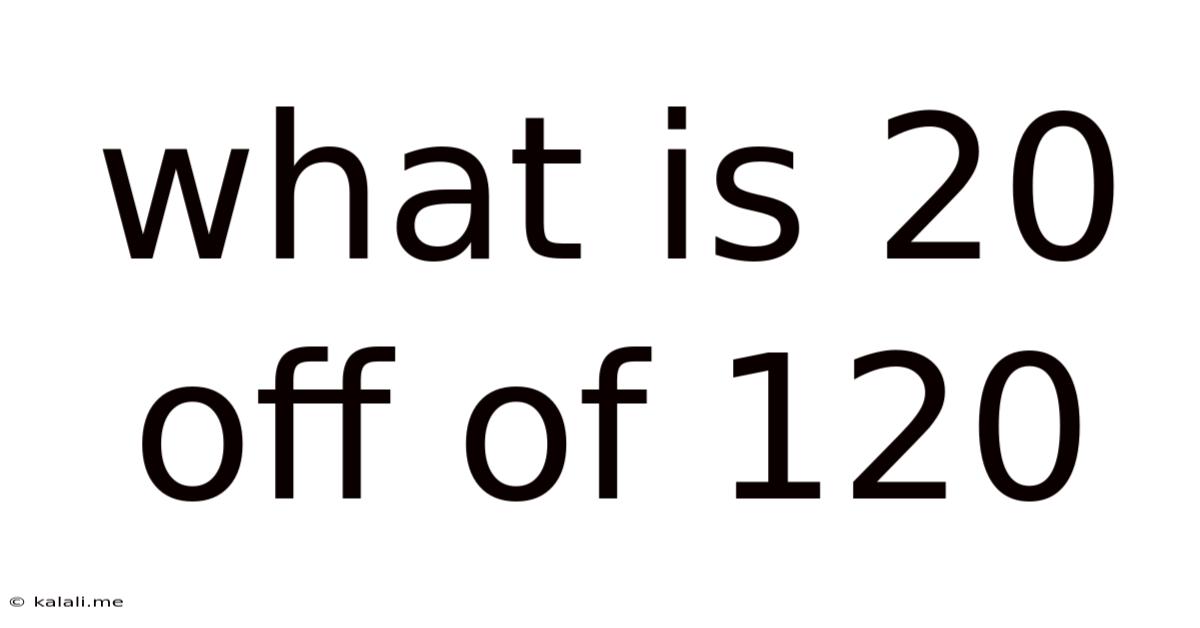
Table of Contents
What is 20% Off of 120? A Comprehensive Guide to Percentage Calculations and Their Applications
This article comprehensively explores the calculation of 20% off of 120, explaining the process step-by-step, providing alternative calculation methods, and delving into the broader applications of percentage calculations in various real-world scenarios. Understanding percentage discounts is crucial for budgeting, shopping, and even financial analysis. Let's dive in!
Meta Description: Learn how to calculate 20% off of 120. This guide provides multiple methods, explains percentage concepts, and shows real-world applications of percentage calculations in various scenarios, including shopping, finance, and more.
What is 20% off of 120?
The simple answer is $96. But how do we arrive at this answer? Let's break down the calculation methodically.
Method 1: Calculating the Discount Amount Directly
This is the most straightforward method. To find 20% of 120, we multiply 120 by 0.20 (which is the decimal equivalent of 20%).
- Convert the percentage to a decimal: 20% = 20/100 = 0.20
- Multiply the original price by the decimal: 120 x 0.20 = 24
- This result (24) represents the discount amount.
- Subtract the discount from the original price: 120 - 24 = 96
Therefore, 20% off of 120 is $96.
Method 2: Calculating the Final Price Directly
This method calculates the final price directly without explicitly calculating the discount amount. We use the fact that if 20% is discounted, then 80% (100% - 20%) remains.
- Find the remaining percentage: 100% - 20% = 80%
- Convert the remaining percentage to a decimal: 80% = 80/100 = 0.80
- Multiply the original price by the decimal representing the remaining percentage: 120 x 0.80 = 96
This directly gives us the final price after the discount, which is $96.
Method 3: Using Fractions
Percentages can also be expressed as fractions. 20% is equivalent to 1/5.
- Convert the percentage to a fraction: 20% = 20/100 = 1/5
- Divide the original price by the denominator of the fraction: 120 / 5 = 24 (this is the discount amount)
- Subtract the discount from the original price: 120 - 24 = 96
This method provides another way to arrive at the final price of $96.
Understanding Percentages: A Deeper Dive
Percentages are a fundamental concept in mathematics and have wide-ranging applications in various fields. They represent a fraction of 100, providing a standardized way to express proportions and ratios. Understanding percentages is vital for:
- Shopping and Sales: Calculating discounts, sales tax, and comparing prices.
- Finance: Calculating interest rates, returns on investments, and loan repayments.
- Statistics and Data Analysis: Representing data proportions, analyzing trends, and making comparisons.
- Science and Engineering: Expressing concentrations, efficiencies, and other quantities.
Key Percentage Concepts
- Percentage Increase: Represents an increase in a value expressed as a percentage of the original value. For example, a 10% increase in a $100 item results in a $110 price.
- Percentage Decrease: Represents a decrease in a value expressed as a percentage of the original value. Our example of 20% off of 120 is a percentage decrease.
- Percentage Points: This refers to the absolute difference between two percentages. For instance, a rise from 10% to 15% is a 5 percentage point increase, not a 50% increase.
Real-World Applications of Percentage Calculations
Let's explore how percentage calculations are used in various everyday situations:
1. Shopping and Retail
- Discount Calculations: This is the most common application. Retailers frequently offer discounts as percentages (e.g., 20% off, 50% off, buy-one-get-one-50%-off). Understanding these calculations helps consumers make informed purchasing decisions and compare prices effectively.
- Sales Tax: Sales tax is usually expressed as a percentage of the purchase price. Calculating the total cost including sales tax requires adding the sales tax percentage to the purchase price.
- Comparing Prices: Percentage calculations help to compare the prices of similar items from different stores or brands, considering any discounts or offers.
2. Finance and Investing
- Interest Rates: Interest rates on loans, savings accounts, and credit cards are expressed as percentages. Understanding interest rate calculations is crucial for managing personal finances and making investment decisions.
- Returns on Investment (ROI): ROI is a key metric for assessing the profitability of investments. It is calculated as a percentage representing the gain or loss relative to the initial investment.
- Inflation: Inflation, the rate at which prices increase over time, is expressed as a percentage. Understanding inflation is crucial for long-term financial planning and investment strategies.
3. Data Analysis and Statistics
- Data Representation: Percentages are frequently used to represent proportions and ratios in data visualizations like pie charts and bar graphs.
- Trend Analysis: Analyzing percentage changes over time helps to identify trends and patterns in data sets.
- Comparative Analysis: Comparing percentages allows for easy comparison of data across different groups or categories.
4. Science and Engineering
- Concentration Calculations: In chemistry, the concentration of solutions is often expressed as a percentage (e.g., percentage by weight, percentage by volume).
- Efficiency Calculations: In engineering, efficiency is often expressed as a percentage, indicating the effectiveness of a process or machine.
- Error Analysis: In scientific experiments, errors are often expressed as percentages to quantify the uncertainty in measurements.
Beyond the Basics: More Complex Percentage Problems
While calculating 20% off of 120 is relatively straightforward, more complex percentage problems might involve multiple discounts, compound interest, or other factors. These problems require a deeper understanding of percentage concepts and the ability to apply them systematically.
Example: Multiple Discounts
Suppose a store offers a 20% discount followed by an additional 10% discount on an item priced at $120. We cannot simply add the percentages (30%) because the second discount is applied to the already reduced price.
- First Discount: 120 x 0.20 = 24 (discount amount) ; 120 - 24 = 96 (price after first discount)
- Second Discount: 96 x 0.10 = 9.60 (discount amount) ; 96 - 9.60 = 86.40 (final price)
The final price after both discounts is $86.40, not $84 (which would be the result of a simple 30% discount).
This example demonstrates the importance of understanding the order of operations and the impact of multiple discounts.
Conclusion
Calculating 20% off of 120, resulting in $96, is a fundamental percentage calculation with broad applications. This article has demonstrated multiple methods for achieving this calculation and explored the importance of understanding percentage concepts in diverse real-world contexts. From everyday shopping to complex financial analysis, mastering percentage calculations is an essential skill. By understanding these principles and practicing various problem types, you can confidently navigate percentage-based scenarios and make informed decisions in various aspects of life.
Latest Posts
Latest Posts
-
Why Are Saturated Fats Solid At Room Temperature
Apr 17, 2025
-
Cuantas Oz Hay En Un Galon
Apr 17, 2025
-
Proteins Are Made Up Of Monomers Called
Apr 17, 2025
-
Is 63 A Prime Number Or A Composite Number
Apr 17, 2025
-
How Many Centimeters Is 50 Inches
Apr 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Off Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.