What Is 20 Off Of 300
Kalali
Apr 25, 2025 · 5 min read
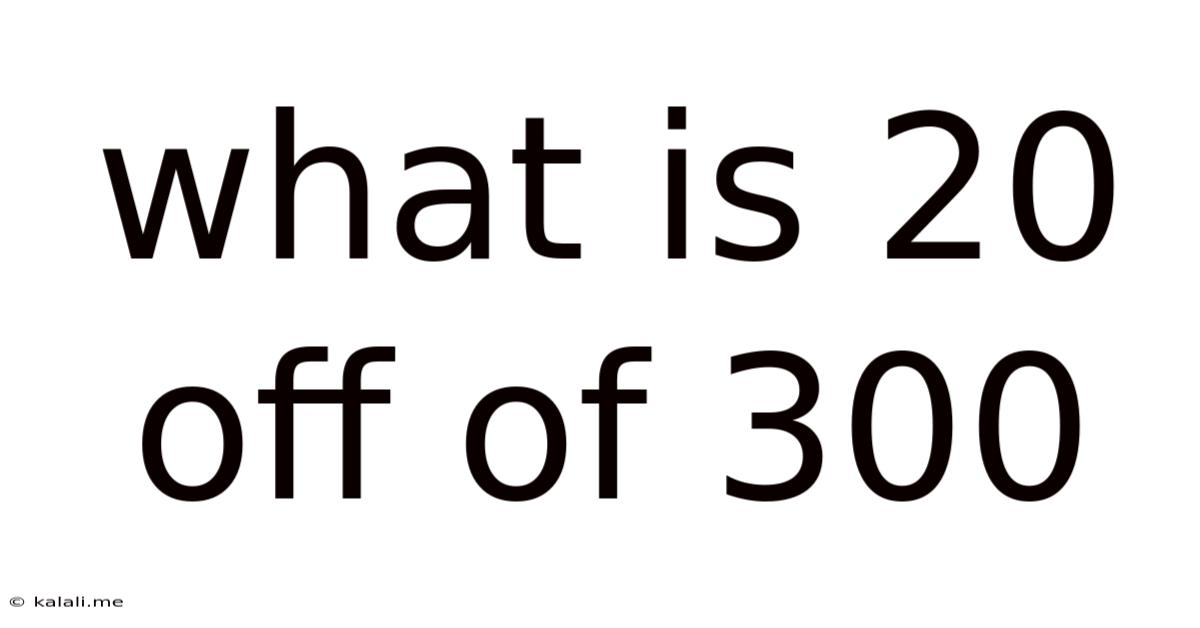
Table of Contents
What is 20% Off of 300? A Comprehensive Guide to Percentage Calculations and Discounts
Calculating discounts is a crucial life skill, whether you're shopping for groceries, planning a big purchase, or simply trying to understand sales promotions. This article will delve into the question: "What is 20% off of 300?" We'll not only provide the answer but also explore the underlying mathematical principles, different calculation methods, and real-world applications of percentage discounts. This guide is designed to be comprehensive, offering a clear understanding of percentage calculations for anyone, regardless of their mathematical background.
Understanding Percentage Discounts
Before we jump into the calculation, let's establish a fundamental understanding of percentage discounts. A percentage discount represents a reduction in the original price of an item or service. It's expressed as a percentage of the original price, indicating the amount you'll save. For instance, a 20% discount on a $300 item means you'll save 20% of $300.
Calculating 20% Off of 300: Method 1 - Finding the Discount Amount First
The most straightforward method involves two steps:
-
Calculate the discount amount: To find 20% of 300, we multiply 300 by 20% (or 0.20, which is the decimal equivalent of 20%).
Discount Amount = 300 x 0.20 = $60 -
Subtract the discount from the original price: Once we know the discount amount ($60), we subtract it from the original price ($300) to find the final price.
Final Price = 300 - 60 = $240
Therefore, 20% off of 300 is $240.
Calculating 20% Off of 300: Method 2 - Finding the Final Price Directly
This method is slightly more efficient. Instead of calculating the discount separately, we directly calculate the final price by finding the remaining percentage (100% - 20% = 80%) and applying it to the original price.
-
Calculate the remaining percentage: Subtract the discount percentage from 100%: 100% - 20% = 80%
-
Calculate the final price: Multiply the original price by the remaining percentage (expressed as a decimal, 0.80):
Final Price = 300 x 0.80 = $240
This method also gives us the final price of $240.
Real-World Applications and Examples
Understanding percentage discounts is essential for making informed purchasing decisions. Here are some real-world examples showcasing the application of this calculation:
-
Retail Sales: Many stores offer seasonal sales or clearance sales with significant discounts. Understanding percentage calculations helps you quickly determine the actual price after the discount. For instance, a 20% off sale on a $300 laptop translates to a final price of $240, as calculated above.
-
Online Shopping: E-commerce platforms frequently feature discount coupons or promotional offers. Being able to calculate the final price after applying a percentage discount is crucial for comparing deals and ensuring you're getting the best value for your money.
-
Tax Calculations: While not directly a discount, understanding percentage calculations is vital when dealing with sales taxes. Sales tax is usually expressed as a percentage of the purchase price, and knowing how to calculate this percentage is essential to determine the total cost of an item.
-
Financial Planning: Percentage calculations are fundamental in personal finance. Understanding interest rates, investment returns, and inflation all rely on the ability to work with percentages. For example, calculating the interest earned on a savings account or the return on an investment involves using percentages.
-
Budgeting: Budgeting often requires calculating percentages of your income to allocate funds for different expenses. For example, you might allocate a certain percentage of your income to housing, transportation, food, and entertainment.
Advanced Percentage Calculations and Scenarios
While the basic calculation of 20% off of 300 is straightforward, let's explore some more complex scenarios involving percentage discounts:
-
Multiple Discounts: Sometimes, you might encounter scenarios with multiple discounts applied successively. For example, a store might offer a 20% discount and then an additional 10% off the already discounted price. In this case, you would apply the discounts sequentially: first calculate the 20% discount, and then apply the 10% discount to the resulting price. This is not simply adding the percentages together (30%).
-
Discounts with Taxes: When a discount is applied before taxes, the tax is calculated on the discounted price. If the discount is applied after taxes, the tax is calculated on the full price, and then the discount is applied. Understanding the order of operations is crucial here.
-
Percentage Increase: While we've focused on discounts (percentage decreases), understanding percentage increases is equally important. For example, if a product's price increases by 10%, you would calculate this increase by multiplying the original price by 1.10.
Troubleshooting Common Errors in Percentage Calculations
Several common mistakes can lead to inaccurate results when calculating percentages:
-
Incorrect Decimal Conversion: Always remember to convert percentages to their decimal equivalents before performing calculations. For example, 20% is 0.20, not 20.
-
Order of Operations: When dealing with multiple discounts or taxes, pay close attention to the order of operations. Applying discounts before taxes will yield a different result than applying them afterward.
-
Confusing Percentage and Decimal: Failing to properly convert between percentages and decimals is a common source of error. Ensure you are working consistently with either percentage or decimal values throughout your calculations to avoid mistakes.
Conclusion: Mastering Percentage Calculations
The ability to quickly and accurately calculate percentage discounts is a valuable skill applicable across various aspects of life. Understanding the fundamental principles and different calculation methods empowers you to make informed decisions when shopping, budgeting, or managing personal finances. While the simple example of "what is 20% off of 300?" provides a basic understanding, this article aims to equip you with a comprehensive knowledge of percentage calculations, enabling you to tackle more complex scenarios with confidence. By mastering percentage calculations, you gain a significant advantage in navigating the numerical world around you.
Latest Posts
Latest Posts
-
How Can I Find The Elevation Of My Home
Apr 25, 2025
-
4 Gallons Equals How Many Liters
Apr 25, 2025
-
How Many Electrons Can The Fourth Energy Level Hold
Apr 25, 2025
-
Glass Breaking Is A Physical Change
Apr 25, 2025
-
What Is The Square Root Of 162
Apr 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Off Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.