What Is 20 Off Of 40
Kalali
Apr 16, 2025 · 6 min read
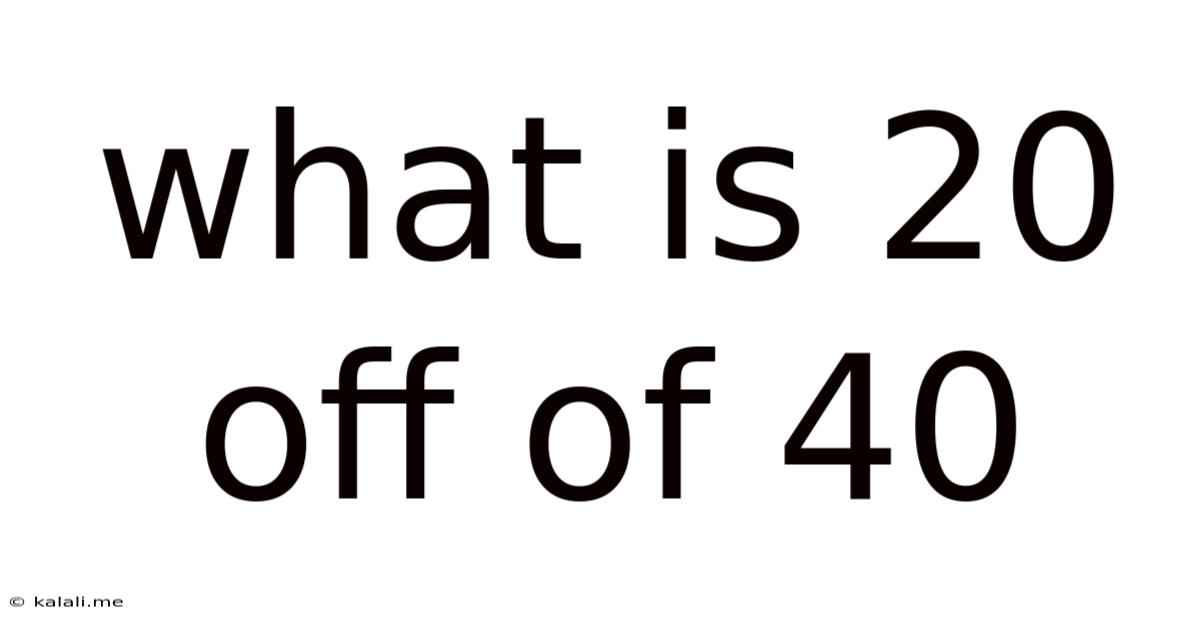
Table of Contents
What is 20% Off of 40? A Comprehensive Guide to Percentage Calculations and Real-World Applications
This seemingly simple question, "What is 20% off of 40?", opens the door to a world of percentage calculations crucial for everyday life, from shopping and budgeting to understanding financial reports and negotiating deals. This guide will not only answer the initial question but also delve into the underlying principles, providing you with the skills to tackle similar percentage problems with ease and confidence. We'll explore various methods of calculation, discuss common pitfalls, and explore real-world applications to solidify your understanding. The meta description for this article is: Learn how to calculate 20% off of 40 and master percentage calculations. We explore various methods, common pitfalls, and real-world applications to make you a percentage pro!
Understanding Percentages
Before diving into the calculation, let's establish a firm grasp of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" denotes "per cent," meaning "out of one hundred." Therefore, 20% can be written as 20/100, or its simplified fraction, 1/5. This signifies that 20% represents 20 parts out of a total of 100 parts.
Method 1: Direct Calculation
The most straightforward approach to finding 20% off of 40 is to calculate 20% of 40 and then subtract the result from 40.
-
Calculate 20% of 40: This can be done by multiplying 40 by the decimal equivalent of 20%, which is 0.20 (or 20/100). So, 40 * 0.20 = 8.
-
Subtract the result from the original amount: This means subtracting the 8 (which represents 20% of 40) from 40. 40 - 8 = 32.
Therefore, 20% off of 40 is $\boxed{32}$.
Method 2: Calculating the Remaining Percentage
Instead of finding the discount and subtracting it, we can directly calculate the remaining percentage (80%) of the original amount.
-
Determine the remaining percentage: If we are taking 20% off, then 100% - 20% = 80% remains.
-
Calculate 80% of 40: Multiply 40 by the decimal equivalent of 80%, which is 0.80 (or 80/100). 40 * 0.80 = 32.
This method also gives us the final answer of $\boxed{32}$.
Method 3: Using Fractions
As mentioned earlier, 20% can be expressed as the fraction 1/5. We can use this fraction to perform the calculation.
-
Express 20% as a fraction: 20% = 1/5
-
Calculate 1/5 of 40: Divide 40 by 5. 40 / 5 = 8. This represents the discount amount.
-
Subtract the discount from the original amount: 40 - 8 = 32.
Again, the final answer is $\boxed{32}$.
Common Pitfalls to Avoid
While percentage calculations might seem straightforward, there are a few common errors to watch out for:
-
Incorrect Decimal Conversion: A frequent mistake is incorrectly converting percentages to decimals. Remember that 20% is 0.20, not 0.2. This seemingly minor error can lead to significantly inaccurate results.
-
Confusing Percentage Increase and Decrease: Understanding whether you're calculating a percentage increase or decrease is vital. Adding a percentage increase directly to the original value, while subtracting a percentage decrease, is crucial.
-
Order of Operations: When dealing with multiple percentage calculations or combined with other mathematical operations, carefully follow the order of operations (PEMDAS/BODMAS) to ensure accuracy.
-
Rounding Errors: When dealing with percentages involving decimals, rounding too early in the calculation can introduce errors in the final answer. It's best to round only at the very end.
Real-World Applications
Understanding percentage calculations is invaluable in various real-life scenarios:
-
Shopping and Sales: Determining the final price after a discount, comparing prices from different stores offering different percentage discounts, and calculating sales tax are common applications. For example, understanding the true savings when an item is marked "50% off, then an additional 20% off" requires multiple percentage calculations.
-
Finance and Budgeting: Calculating interest on loans, savings accounts, and investments; understanding annual percentage rates (APR); tracking monthly expenses as percentages of income; and analyzing financial statements all require a strong grasp of percentages.
-
Tipping and Gratuities: Calculating tips in restaurants based on a percentage of the bill is a common everyday use case.
-
Tax Calculations: Calculating sales tax, income tax, and other taxes often involves percentage calculations.
-
Data Analysis: Representing data as percentages in graphs, charts, and reports makes the data more readily understandable.
-
Negotiations: When negotiating prices, discounts, or salaries, understanding percentages is crucial to assess the value of an offer and reach a favorable outcome. For example, negotiating a 15% discount on a $1000 item requires a precise percentage calculation.
-
Understanding Statistics and Probability: Percentages are fundamental to understanding statistical data and probabilities. For instance, understanding that a 95% confidence interval in a survey means there is a 95% chance that the true value falls within a certain range relies on percentage comprehension.
Advanced Percentage Calculations
While the initial question was simple, mastering percentage calculations involves tackling more complex problems. These often involve multiple percentage changes or combined with other mathematical operations.
Scenario 1: Multiple Discounts
Imagine a store offering a 20% discount followed by an additional 10% discount. This isn't simply a 30% discount. Let's use an example of a $40 item:
-
First discount: 20% off $40 = $40 * 0.20 = $8. The price becomes $40 - $8 = $32.
-
Second discount: 10% off $32 = $32 * 0.10 = $3.20. The final price becomes $32 - $3.20 = $28.80.
Notice that the second discount is applied to the already reduced price.
Scenario 2: Percentage Increase
Suppose you want to increase a value by a certain percentage. For instance, increasing $40 by 15%:
-
Calculate the increase: $40 * 0.15 = $6.
-
Add the increase to the original value: $40 + $6 = $46.
Scenario 3: Finding the Original Price
If you know the final price after a discount, you can work backward to find the original price. For example, if an item costs $32 after a 20% discount:
-
Determine the remaining percentage: 100% - 20% = 80%
-
Set up an equation: 0.80 * x = $32, where x is the original price.
-
Solve for x: x = $32 / 0.80 = $40.
Conclusion
The seemingly simple question, "What is 20% off of 40?" serves as an excellent entry point to understanding the world of percentage calculations. By mastering the various methods and avoiding common pitfalls, you can confidently tackle percentage problems in various real-world scenarios. Remember to practice regularly and apply your knowledge in everyday situations to build your proficiency. From budgeting and shopping to analyzing financial data and negotiating deals, a strong understanding of percentages is a valuable skill that will serve you well throughout your life. The ability to quickly and accurately perform percentage calculations will enhance your decision-making capabilities and empower you to make informed choices.
Latest Posts
Latest Posts
-
How Many Centimeters Are In A Meter Stick
Jul 10, 2025
-
Why Did The Orchestra Get An R Rating
Jul 10, 2025
-
Is 27 A Prime Or Composite Number
Jul 10, 2025
-
What Is Double Of 1 4 Cup
Jul 10, 2025
-
Prepare Me A Body And I Will Redeem Man
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Off Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.