What Is 20 Percent Of 250 000
Kalali
Aug 20, 2025 · 5 min read
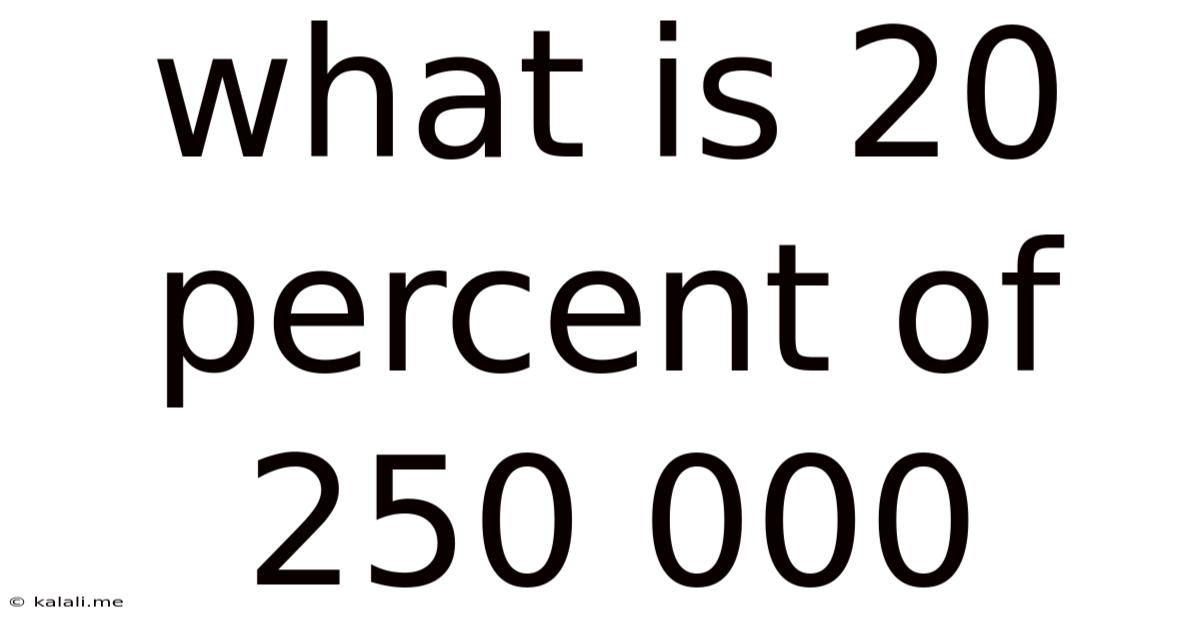
Table of Contents
What is 20 Percent of 250,000? A Comprehensive Guide to Percentage Calculations
Finding 20 percent of 250,000 might seem like a simple calculation, but understanding the underlying principles of percentage calculations is crucial for various applications, from budgeting and finance to sales and statistics. This comprehensive guide will not only answer the question directly but also delve into the methods, applications, and related concepts of percentage calculations, equipping you with a solid understanding of this fundamental mathematical skill.
Meta Description: Learn how to calculate 20% of 250,000 and master percentage calculations. This guide covers various methods, real-world applications, and related concepts, providing a comprehensive understanding of percentages.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote percentage. It represents a portion of a whole. For instance, 20% means 20 out of 100, or 20/100, which simplifies to 1/5. Understanding this fundamental concept is key to solving any percentage problem.
Methods for Calculating 20% of 250,000
There are several ways to calculate 20% of 250,000. Let's explore the most common approaches:
Method 1: Using Decimal Conversion
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent by dividing by 100. 20% becomes 0.20 (or simply 0.2). Then, we multiply this decimal by the number we're finding the percentage of:
250,000 x 0.2 = 50,000
Therefore, 20% of 250,000 is 50,000.
Method 2: Using Fractions
As mentioned earlier, 20% is equivalent to the fraction 1/5. We can calculate 20% of 250,000 by dividing 250,000 by 5:
250,000 / 5 = 50,000
This method is particularly useful when dealing with percentages that have easy fractional equivalents, such as 25% (1/4), 50% (1/2), and 75% (3/4).
Method 3: Using Proportion
This method uses the concept of ratios and proportions. We can set up a proportion to solve for the unknown value (x), representing 20% of 250,000:
20/100 = x/250,000
To solve for x, we cross-multiply:
100x = 20 * 250,000
100x = 5,000,000
x = 5,000,000 / 100
x = 50,000
This confirms that 20% of 250,000 is 50,000.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life. Here are some examples:
-
Finance: Calculating interest on loans or investments, determining discounts on purchases, analyzing financial statements, and understanding tax rates all involve percentage calculations. For example, if a bank offers a 5% interest rate on a savings account with a balance of 250,000, the interest earned in a year would be 12,500 (250,000 x 0.05).
-
Sales and Marketing: Calculating sales tax, determining profit margins, understanding discounts and markups, analyzing market share, and tracking conversion rates all rely on percentage calculations. A 20% discount on a 250,000 item would reduce the price by 50,000.
-
Statistics: Percentages are fundamental to representing data and interpreting statistical results. For example, expressing survey results, calculating probabilities, and analyzing population demographics often involve percentages. If 20% of a population of 250,000 people voted for a specific candidate, that would mean 50,000 votes.
-
Science: Percentages are used to express concentrations of solutions, calculating yields in chemical reactions, and representing data in scientific experiments.
-
Everyday Life: Tips in restaurants (e.g., a 20% tip on a $100 bill), calculating sale prices, and determining the percentage of completion on projects all involve percentage calculations.
Calculating Other Percentages of 250,000
Understanding the methods above allows you to easily calculate any percentage of 250,000. For example:
- 5% of 250,000: 250,000 x 0.05 = 12,500
- 15% of 250,000: 250,000 x 0.15 = 37,500
- 30% of 250,000: 250,000 x 0.30 = 75,000
- 75% of 250,000: 250,000 x 0.75 = 187,500
- 100% of 250,000: 250,000 x 1 = 250,000
Advanced Percentage Calculations: Finding the Original Value
Sometimes, you know the percentage and the resulting value, and you need to find the original value. For example, if 20% of a number is 50,000, what is the original number?
Here's how to solve this:
Let 'x' be the original number. We can set up the equation:
0.20x = 50,000
To solve for x, we divide both sides by 0.20:
x = 50,000 / 0.20
x = 250,000
This demonstrates the reverse calculation—finding the original value given a percentage and its corresponding value.
Percentage Increase and Decrease
Percentage increase and decrease calculations are also commonly used. These calculations involve finding the difference between two values and expressing that difference as a percentage of the original value.
Percentage Increase: [(New Value - Original Value) / Original Value] x 100%
Percentage Decrease: [(Original Value - New Value) / Original Value] x 100%
For instance, if a value increases from 200,000 to 250,000, the percentage increase is:
[(250,000 - 200,000) / 200,000] x 100% = 25%
Using Calculators and Spreadsheets for Percentage Calculations
While manual calculations are useful for understanding the underlying principles, calculators and spreadsheet software like Microsoft Excel or Google Sheets can significantly simplify complex percentage calculations. These tools offer built-in functions for calculating percentages, making calculations faster and more efficient, especially when dealing with large datasets or intricate calculations.
Conclusion
Calculating 20% of 250,000 is a fundamental percentage calculation with numerous applications across various fields. This guide has detailed multiple methods for performing this calculation, explained the underlying principles of percentage calculations, and explored real-world applications. Mastering percentage calculations is a valuable skill that enhances your understanding of numerical data and improves your problem-solving abilities in diverse contexts. Remember to choose the method that best suits your needs and utilize tools like calculators and spreadsheets to streamline the process when dealing with more complex scenarios. Understanding percentages is a crucial skill for navigating the complexities of the modern world, from personal finance to professional endeavors.
Latest Posts
Latest Posts
-
What Year Are You Born In If Your 13
Aug 20, 2025
-
Where Can I Watch One Night In Paris
Aug 20, 2025
-
How Many 16 Fl Oz In A Gallon
Aug 20, 2025
-
How Long Is 5 Semesters In College
Aug 20, 2025
-
Mix My Milk With Your Cocoa Puffs
Aug 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Percent Of 250 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.