What Is 20 Percent Of 88
Kalali
Apr 13, 2025 · 6 min read
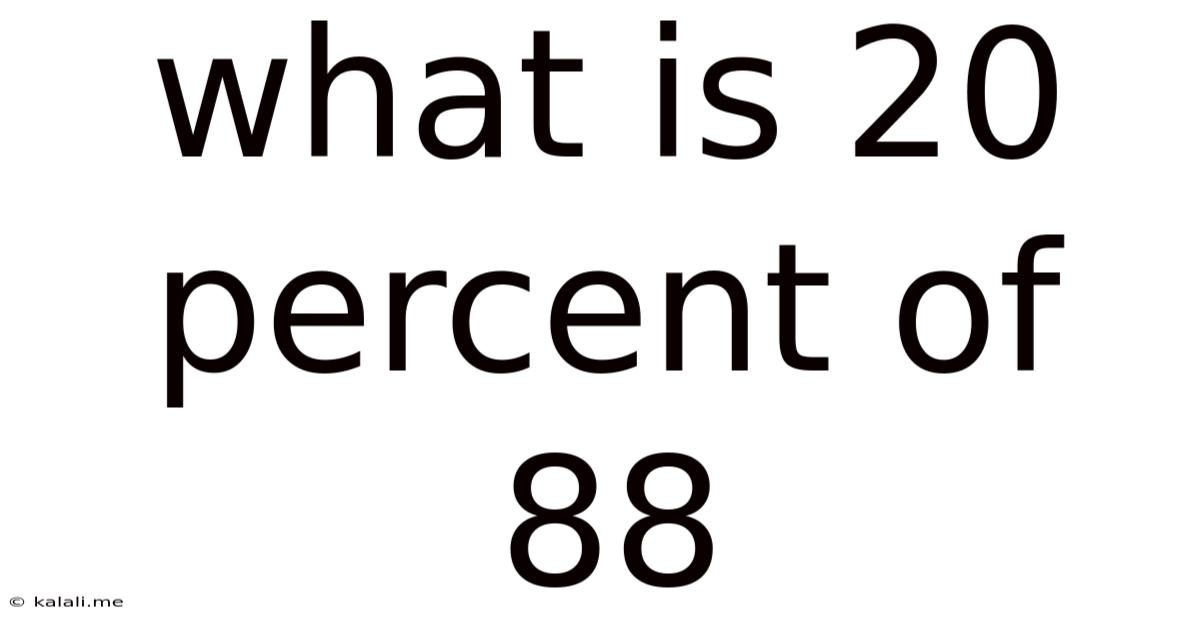
Table of Contents
What is 20 Percent of 88? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 88 might seem like a simple calculation, readily solvable with a calculator. However, understanding the underlying principles of percentages and their diverse applications opens up a world of possibilities beyond this single numerical problem. This article delves into the mechanics of percentage calculations, explores various methods to solve this specific problem, and showcases the practical relevance of percentages in everyday life and various professional fields. The meta description for this article would be: Learn how to calculate 20% of 88 and master percentage calculations. Discover real-world applications of percentages in finance, statistics, and more.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (from the Latin per centum). Therefore, 20 percent can be represented as 20/100, 0.20, or 20%. These representations are all equivalent and interchangeable. Understanding this fundamental concept is crucial for accurately performing percentage calculations.
Percentages are a powerful tool because they allow for easy comparison of proportions across different quantities. Whether comparing sales growth, survey responses, or discount rates, percentages offer a standardized method for interpreting relative magnitudes.
Calculating 20 Percent of 88: Three Different Approaches
There are several ways to calculate 20 percent of 88. Let's explore three common methods:
1. The Decimal Method:
This is arguably the most straightforward approach. Convert the percentage to its decimal equivalent (20% = 0.20) and multiply it by the number:
0.20 * 88 = 17.6
Therefore, 20 percent of 88 is 17.6. This method is efficient and easily adaptable to different percentage calculations.
2. The Fraction Method:
Representing 20 percent as a fraction (20/100, which simplifies to 1/5) allows for a different calculation:
(1/5) * 88 = 88/5 = 17.6
This method demonstrates the core relationship between fractions and percentages, offering another perspective on the calculation. It's particularly useful when dealing with percentages that translate into simple fractions.
3. The Proportion Method:
This method is useful for understanding the proportional relationship between the percentage and the whole. We can set up a proportion:
20/100 = x/88
Where 'x' represents 20 percent of 88. To solve for 'x', cross-multiply:
100x = 20 * 88 100x = 1760 x = 1760/100 x = 17.6
This method highlights the underlying proportional relationships and is particularly helpful for visualizing percentage problems.
Real-World Applications of Percentage Calculations
Percentage calculations aren't confined to mathematical exercises; they are essential tools in numerous real-world contexts. Let’s explore some examples:
1. Finance:
- Interest Calculations: Banks and financial institutions use percentages extensively to calculate interest on loans, savings accounts, and investments. Understanding percentage calculations is crucial for managing personal finances and making informed financial decisions. For instance, calculating the interest accrued on a savings account or the total cost of a loan, including interest, necessitates proficiency in percentage computations.
- Discounts and Sales Tax: Retailers frequently advertise discounts as percentages (e.g., "20% off"). Calculating the final price after a discount or adding sales tax (expressed as a percentage) requires a solid grasp of percentage calculations.
- Investment Returns: Investors monitor the performance of their investments by calculating percentage returns. Understanding percentage changes helps investors track their investment growth or losses over time.
2. Statistics and Data Analysis:
- Data Representation: Percentages are frequently used to represent proportions in data sets. For example, in surveys or polls, responses are often presented as percentages of the total sample size. This provides a readily understandable representation of the data.
- Statistical Measures: Percentages are integral to various statistical measures like percentage change, percentage point change, and relative frequency. These measures are essential for analyzing trends, making comparisons, and drawing conclusions from data.
3. Everyday Life:
- Tip Calculations: Calculating tips in restaurants often involves estimating a percentage (e.g., 15% or 20%) of the total bill.
- Recipe Scaling: Adjusting recipes to accommodate different serving sizes involves using percentages to increase or decrease ingredient quantities proportionally.
- Sales and Bargain Hunting: Understanding percentage discounts is crucial for making informed purchasing decisions and finding the best deals.
4. Science and Engineering:
- Error Analysis: In scientific experiments and engineering projects, percentage errors are commonly used to quantify the accuracy of measurements and calculations.
- Efficiency Calculations: In engineering and manufacturing, percentage efficiency is a key metric for evaluating the effectiveness of processes and systems.
5. Business and Management:
- Profit Margins: Businesses calculate profit margins as a percentage of revenue to assess profitability and financial performance.
- Market Share Analysis: Companies track their market share (the percentage of total market sales) to gauge their competitive position.
- Growth Rates: Percentage growth rates are used to track the progress of a business over time, whether it’s revenue growth, customer acquisition, or market expansion.
Beyond the Basics: Advanced Percentage Concepts
While calculating 20% of 88 provides a fundamental understanding of percentages, more complex scenarios often arise. Understanding these advanced concepts broadens your proficiency in percentage-based calculations:
- Percentage Increase/Decrease: Calculating the percentage change between two values (e.g., determining the percentage increase in sales from one year to the next) involves subtracting the initial value from the final value, dividing by the initial value, and multiplying by 100.
- Percentage Point Change: This is crucial in scenarios where you are comparing percentage changes. A percentage point change represents the absolute difference between two percentages, whereas a percentage change refers to the relative change. For instance, a change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase.
- Compounding Percentages: When percentages are applied repeatedly (e.g., compound interest), the calculation becomes more complex, requiring iterative application of the percentage.
- Reverse Percentage Calculations: Finding the original value given a percentage and the resulting value (e.g., if an item costs $17.60 after a 20% discount, what was the original price?) requires working backward using the percentage and the final value.
Mastering these advanced concepts enables a deeper understanding of how percentages function in complex situations and allows for effective problem-solving in various fields.
Conclusion
While the simple calculation of "what is 20 percent of 88?" (17.6) might appear trivial, it serves as a gateway to understanding the broader significance of percentage calculations. Percentages are essential tools in numerous aspects of life, from personal finance to scientific research and business management. By understanding the different methods of calculating percentages and exploring their diverse applications, you equip yourself with a valuable skill set applicable across a wide range of fields. Proficiency in percentage calculations is not merely a mathematical skill; it’s a practical competency that enhances decision-making and problem-solving abilities in both personal and professional domains.
Latest Posts
Latest Posts
-
225 Minutes Is How Many Hours
Apr 15, 2025
-
Convert 93 Degrees Fahrenheit To Celsius
Apr 15, 2025
-
What Is 4 To The 0 Power
Apr 15, 2025
-
How Many Hours Is 372 Minutes
Apr 15, 2025
-
The Particles In A Crystalline Solid Are Arranged
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Percent Of 88 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.