What Is 24 Percent Of 60
Kalali
Apr 27, 2025 · 4 min read
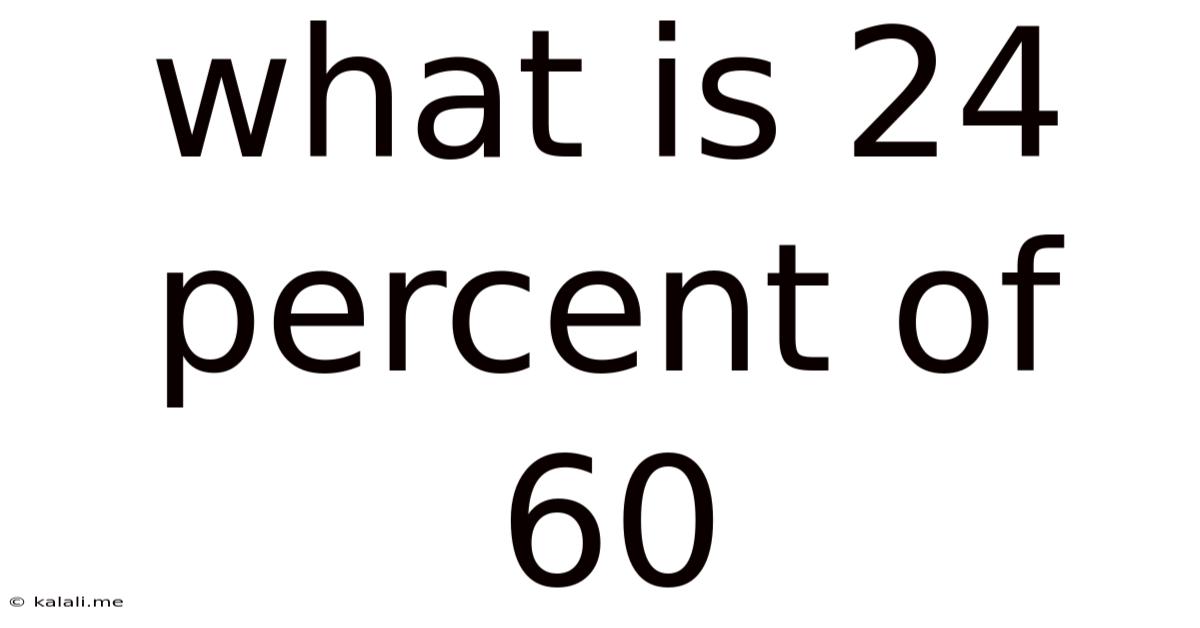
Table of Contents
What is 24 Percent of 60? A Deep Dive into Percentage Calculations
This seemingly simple question, "What is 24 percent of 60?", opens the door to a fascinating exploration of percentage calculations, their real-world applications, and the underlying mathematical principles. While the answer itself is easily obtained through a simple calculation, understanding the how and why behind the calculation is crucial for anyone looking to master percentage-based problem-solving, a skill applicable across various fields from finance and statistics to everyday shopping and cooking. This article will not only provide the answer but also delve into the various methods for calculating percentages, exploring different approaches and highlighting their usefulness in diverse contexts.
Understanding Percentages: The Foundation
Percentages are simply fractions expressed as parts of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 24 percent (24%) means 24 parts out of 100, or 24/100. This foundational understanding is key to grasping how percentage calculations work. Think of a percentage as a ratio – a comparison of two numbers. In this case, we're comparing 24 to 100.
Method 1: The Classic Formula
The most common method for calculating percentages is using the basic formula:
(Percentage/100) * Whole Number = Part
In our case:
(24/100) * 60 = 14.4
Therefore, 24 percent of 60 is 14.4. This method is straightforward and easy to understand, making it suitable for beginners and quick calculations. The formula clearly shows the relationship between the percentage, the whole number, and the resulting part.
Method 2: Using Decimal Equivalents
A percentage can be easily converted into a decimal by dividing it by 100. 24% becomes 0.24. This allows us to simplify the calculation:
Decimal Equivalent * Whole Number = Part
0.24 * 60 = 14.4
This method is computationally efficient, especially when working with multiple percentage calculations or using calculators. The conversion to decimals streamlines the process, making it faster and less prone to errors.
Method 3: Proportion Method
This method is particularly useful for visualizing the relationship between the parts and the whole. We set up a proportion:
24/100 = x/60
Here, 'x' represents the unknown value (24% of 60). To solve for 'x', we cross-multiply:
100x = 24 * 60
100x = 1440
x = 1440/100
x = 14.4
The proportion method offers a clear visual representation of the problem, making it easier to grasp the underlying concept. It's especially beneficial for teaching percentage calculations to students.
Real-World Applications: Where Percentages Matter
Understanding percentage calculations is essential in a multitude of real-world situations. Here are just a few examples:
-
Finance: Calculating interest rates, discounts, taxes, profits, and losses all involve percentages. For example, understanding how much a 24% discount on a $60 item would save you is a direct application of this calculation.
-
Statistics: Percentages are fundamental in presenting and interpreting data. They allow us to express proportions and trends clearly and concisely. Understanding survey results, election polls, and market research often requires working with percentages.
-
Retail and Sales: Calculating discounts, markups, sales tax, and profit margins are all crucial aspects of retail business, heavily reliant on percentage calculations.
-
Everyday Life: Calculating tips at restaurants, understanding sale prices, or determining the nutritional content of food all involve working with percentages. Even determining the percentage of completion on a project relies on this basic mathematical principle.
Beyond the Basics: More Complex Percentage Problems
While the question "What is 24 percent of 60?" provides a straightforward introduction to percentage calculations, the applications extend far beyond simple arithmetic. Consider these more complex scenarios:
-
Finding the percentage increase or decrease: Imagine a product initially costing $60, and its price increased by 24%. This involves calculating the increase amount (14.4) and adding it to the original price. Conversely, if the price decreased by 24%, you would subtract 14.4 from the original price.
-
Calculating the original amount: If you know that 24% of an unknown amount is 14.4, you can work backward to find the original amount using algebraic equations.
-
Compound percentages: These scenarios involve applying percentages repeatedly, often seen in compound interest calculations.
Expanding Your Knowledge: Further Exploration
Mastering percentages requires consistent practice and exploration. Here are some suggestions for further enhancing your understanding:
-
Practice diverse problems: Work through various percentage problems, incorporating different scenarios and complexities.
-
Use online resources: Many online calculators and educational websites provide practice problems and explanations.
-
Utilize real-world examples: Apply your knowledge to real-life scenarios, such as calculating discounts or interest rates.
-
Explore advanced concepts: Delve into compound interest, percentage change, and other more complex percentage applications.
Conclusion: The Power of Percentage Calculations
The seemingly simple calculation of "What is 24 percent of 60?" serves as a gateway to a vast world of mathematical applications. Understanding percentages is not only a valuable skill for academic pursuits but also a fundamental tool for navigating various aspects of daily life and professional endeavors. By mastering these fundamental principles and practicing regularly, you can unlock the power of percentage calculations and confidently tackle complex problems across diverse fields. Remember the basic formula, explore different calculation methods, and apply your knowledge to real-world examples to solidify your understanding and unlock the full potential of percentage calculations.
Latest Posts
Latest Posts
-
How Much Is 77 Inches In Feet
Apr 28, 2025
-
8 Cups Of Water In Ml
Apr 28, 2025
-
4 1 4 As An Improper Fraction
Apr 28, 2025
-
Cuales Son Los Centimetros En Un Metro
Apr 28, 2025
-
How Much Is 170 Cm In Inches
Apr 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 24 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.