What Is 25 Percent Of 150
Kalali
Apr 14, 2025 · 6 min read
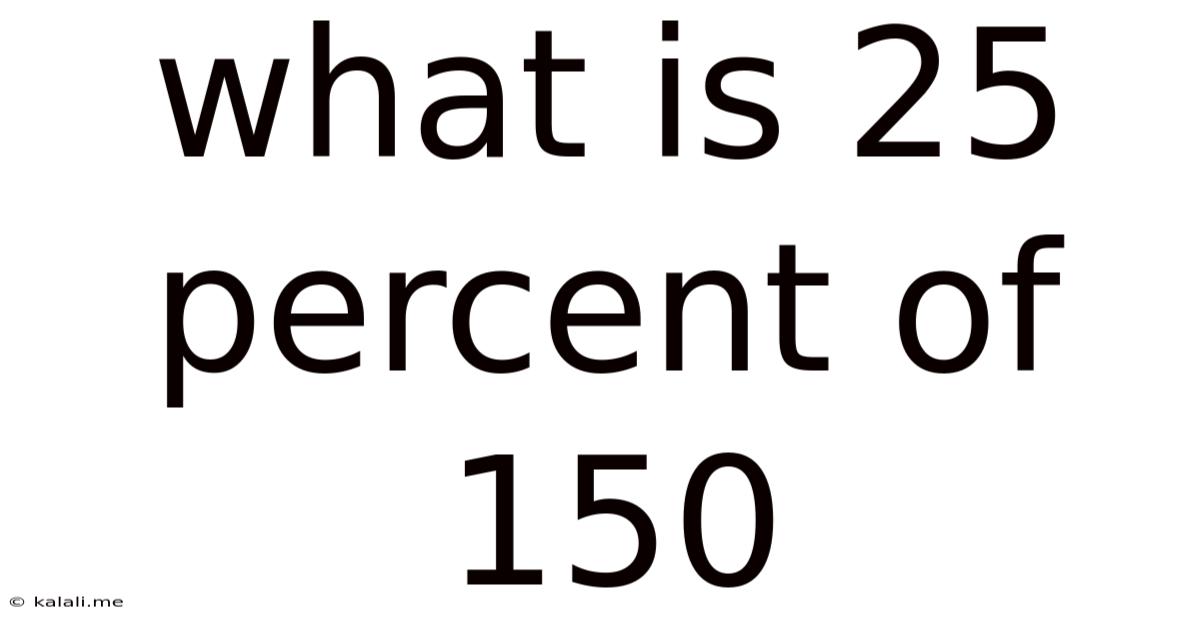
Table of Contents
What is 25 Percent of 150? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 25 percent of 150?", opens the door to a vast world of mathematical concepts and practical applications. Understanding percentages is crucial in numerous aspects of life, from calculating discounts and taxes to analyzing financial statements and understanding statistical data. This article will not only answer the initial question but also explore the underlying principles of percentage calculations, different methods for solving percentage problems, and real-world examples of their usage. This comprehensive guide aims to solidify your understanding of percentages and equip you with the tools to tackle various percentage-related challenges.
Meta Description: Discover how to calculate 25% of 150 and delve into the broader world of percentages. Learn various calculation methods, explore real-world applications, and master percentage problems with this comprehensive guide.
The Quick Answer: 25% of 150
Before we dive into the intricacies of percentage calculations, let's answer the core question directly: 25% of 150 is 37.5.
Understanding Percentages: A Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" is derived from the Latin words "per centum," meaning "out of a hundred." Therefore, 25% can be written as 25/100 or 0.25 as a decimal. This representation is key to understanding how percentage calculations work.
Methods for Calculating Percentages
There are several ways to calculate percentages, each with its own advantages depending on the context and the individual's preference. Let's explore three common approaches:
1. The Fraction Method
This method utilizes the fundamental definition of percentage. To find 25% of 150, we first convert the percentage to a fraction:
- 25% = 25/100
Then, we multiply this fraction by the number:
- (25/100) * 150 = 37.5
This method is straightforward and helps visualize the relationship between the percentage and the whole number. It's especially useful for simple percentage calculations.
2. The Decimal Method
This approach converts the percentage to a decimal and then multiplies it by the number. Converting 25% to a decimal gives us 0.25. The calculation then becomes:
- 0.25 * 150 = 37.5
This method is often preferred for its efficiency, particularly when using calculators. The decimal method is widely used in various applications involving percentages.
3. The Proportion Method
This method sets up a proportion to solve for the unknown value. We can represent the problem as:
- 25/100 = x/150
To solve for x (25% of 150), we cross-multiply:
- 25 * 150 = 100 * x
- 3750 = 100x
- x = 3750 / 100
- x = 37.5
This method is particularly helpful when dealing with more complex percentage problems or when working with ratios and proportions. It provides a systematic approach that can be easily adapted to different scenarios.
Real-World Applications of Percentage Calculations
Percentages permeate various aspects of our daily lives and professional endeavors. Here are a few examples:
1. Sales and Discounts
Retail stores frequently offer discounts as percentages. For instance, a "25% off" sale means that the price is reduced by 25% of the original price. If an item costs $150 and has a 25% discount, the discount amount is $37.5 (as calculated earlier), and the final price would be $150 - $37.5 = $112.5.
Understanding percentage discounts is crucial for making informed purchasing decisions and comparing prices between different stores or products. The ability to quickly calculate these discounts can save you significant money over time.
2. Taxes and Interest
Governments levy taxes on income, goods, and services, often expressed as percentages. For example, a 6% sales tax on a $150 purchase would add $9 (6% of $150) to the final cost. Similarly, interest rates on loans and savings accounts are usually expressed as percentages.
Understanding how taxes and interest are calculated is vital for managing personal finances effectively. Accurate calculations ensure you are paying the correct amount in taxes or receiving the expected returns on your investments. This knowledge empowers you to make sound financial decisions and avoid unnecessary financial burdens.
3. Financial Statements and Analysis
Percentages are fundamental in analyzing financial statements like income statements and balance sheets. For instance, profit margins, return on investment (ROI), and debt-to-equity ratios are all expressed as percentages. These ratios provide valuable insights into a company's financial health and performance.
The ability to analyze these financial metrics is crucial for both investors and business owners. Understanding percentage changes in revenue, expenses, and profits helps make informed business decisions, identify areas for improvement, and predict future financial performance.
4. Statistics and Data Analysis
Percentages are commonly used in statistical analysis to present data in a clear and concise manner. For example, survey results, election polls, and scientific studies often express their findings in percentages. This allows for easy comparison and interpretation of data.
Understanding how percentages are used in statistical analysis allows for a more critical and informed understanding of research findings. It helps interpret complex data sets and draws meaningful conclusions from various sources of information. This skill is increasingly relevant in today's data-driven world.
5. Tip Calculation
Calculating tips in restaurants is a common application of percentages. A common practice is to leave a 15% to 20% tip. If the bill is $150, a 15% tip would be $22.50 (15% of $150).
Knowing how to calculate tips quickly and accurately is essential for demonstrating good etiquette and making fair payments in service industries. This simple skill enhances social interactions and helps maintain positive relationships with service providers.
Beyond the Basics: Advanced Percentage Problems
While the problem of finding 25% of 150 is relatively straightforward, percentage calculations can become more complex. Here are some examples of more advanced scenarios:
- Finding the original amount: If an item is discounted by 25% and costs $112.50 after the discount, how much was the original price?
- Calculating percentage increase or decrease: What is the percentage increase or decrease if a value changes from 100 to 150?
- Compound percentages: Calculating the effect of multiple percentages applied successively (e.g., applying a discount and then a sales tax).
Solving these more advanced problems requires a solid understanding of the fundamental principles of percentages and the ability to apply the appropriate calculation methods. Practice and exposure to various problems are crucial for developing proficiency in solving these more challenging scenarios.
Conclusion: Mastering Percentages for a Data-Driven World
The seemingly simple question, "What is 25 percent of 150?", has led us on a journey exploring the world of percentages. We've seen how percentages are fundamental to numerous aspects of life, from everyday transactions to complex financial analysis. Mastering percentage calculations is a valuable skill that empowers you to make informed decisions, analyze data critically, and navigate the increasingly data-driven world around us. Remember the various methods discussed – fraction, decimal, and proportion – and choose the approach that best suits your needs and the complexity of the problem. With practice and a firm grasp of the underlying principles, you'll be well-equipped to tackle any percentage-related challenge with confidence.
Latest Posts
Latest Posts
-
Which Point Is A Solution To The System
Apr 15, 2025
-
4 Inches Equals How Many Millimeters
Apr 15, 2025
-
How To Focus A Microscope Using High Power Lens
Apr 15, 2025
-
What Is 9 5 Inches In Cm
Apr 15, 2025
-
How Much Is 155 Cm In Feet
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Percent Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.