What Is 27 Out Of 30 As A Percentage
Kalali
Apr 15, 2025 · 5 min read
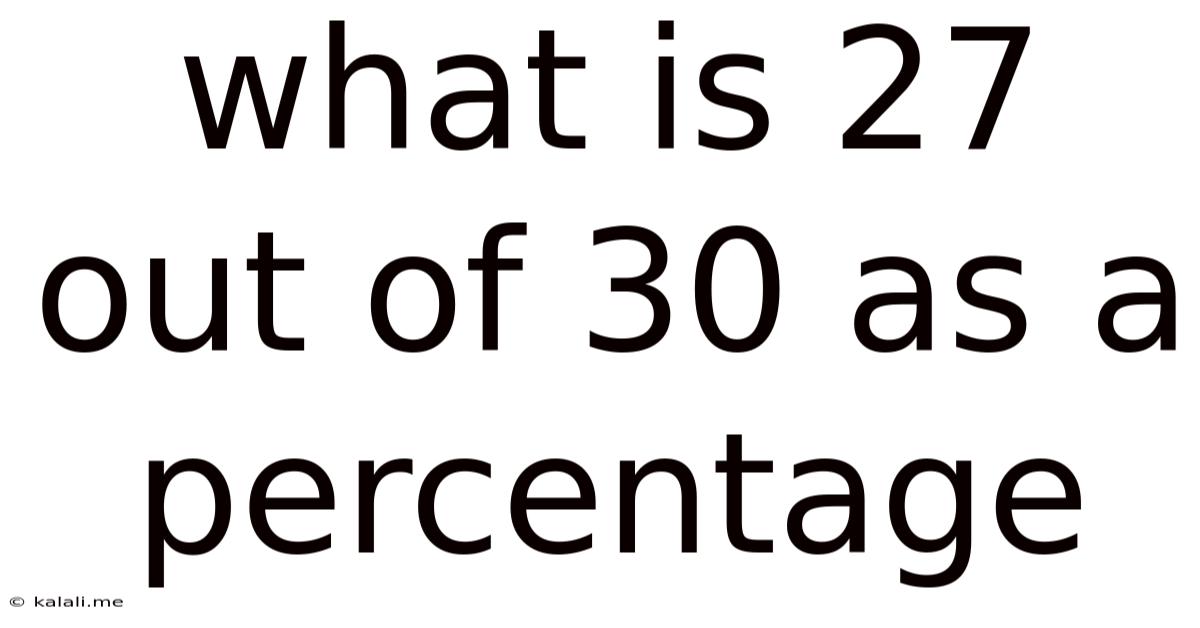
Table of Contents
What is 27 out of 30 as a Percentage? A Comprehensive Guide to Percentage Calculations
This article will comprehensively answer the question: "What is 27 out of 30 as a percentage?" We'll not only provide the answer but also delve into the underlying principles of percentage calculations, offering various methods to solve similar problems, and explore practical applications of percentages in everyday life. Understanding percentages is a fundamental skill with wide-ranging applications in various fields, from finance and statistics to everyday shopping and grading systems.
Meta Description: Learn how to calculate percentages with a detailed explanation of how to find the percentage equivalent of 27 out of 30. This guide covers various methods, real-world examples, and practical applications of percentage calculations.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" ("per" meaning "for each" and "cent" meaning "hundred"). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Percentages are a common way to represent proportions, ratios, and rates of change. They offer a standardized way to compare different quantities and easily grasp relative sizes.
Method 1: The Fraction Method
The most straightforward approach to calculating "27 out of 30 as a percentage" involves converting the given numbers into a fraction and then expressing that fraction as a percentage.
-
Form a Fraction: Represent "27 out of 30" as a fraction: 27/30.
-
Convert to Decimal: Divide the numerator (27) by the denominator (30): 27 ÷ 30 = 0.9
-
Convert to Percentage: Multiply the decimal by 100: 0.9 × 100 = 90%
Therefore, 27 out of 30 is 90%.
Method 2: The Proportion Method
This method uses the concept of proportions to solve the problem. We set up a proportion where x represents the unknown percentage:
27/30 = x/100
To solve for x, we cross-multiply:
30x = 2700
Then, divide both sides by 30:
x = 2700 ÷ 30 = 90
Therefore, x = 90%, confirming our previous result. This method is particularly useful when dealing with more complex percentage problems.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the process. Simply enter 27 ÷ 30 and then multiply the result by 100. The calculator will directly display the answer as 90%. This method is the quickest and most efficient for simple percentage calculations.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of life:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentages is crucial for making informed financial decisions. For example, calculating the interest earned on a savings account or determining the total cost of an item after sales tax involves percentage computations.
-
Statistics: Percentages are used extensively in statistical analysis to represent data proportions, trends, and probabilities. For instance, expressing survey results, analyzing demographic data, or calculating the percentage of students passing an exam requires using percentages. Analyzing market share data and understanding the growth rate of a business also depends heavily on percentage calculations.
-
Grades and Assessments: Educational institutions use percentages to represent student performance on exams and assignments. Understanding the percentage grade received helps students assess their performance and identify areas for improvement. Teachers and educational institutions utilize percentages for calculating overall grades and identifying trends in student achievement.
-
Shopping and Sales: Sales discounts are expressed as percentages, enabling consumers to quickly determine the final price after the discount. Understanding percentage discounts is critical for making budget-friendly purchasing decisions. Similarly, comparing prices of similar items with different discounts requires percentage calculations.
-
Health and Nutrition: Nutritional labels often display the percentage of daily recommended values for various nutrients. Understanding these percentages helps individuals make informed dietary choices and maintain a balanced diet. Similarly, health statistics and epidemiological data often utilize percentages to present disease prevalence, incidence, and mortality rates.
Solving Similar Percentage Problems
Let's consider some variations on the original problem to illustrate the versatility of the methods described:
-
What is 18 out of 24 as a percentage?
Following the fraction method: 18/24 = 0.75, and 0.75 × 100 = 75%.
-
What is 35 out of 50 as a percentage?
Using the proportion method: 35/50 = x/100; 50x = 3500; x = 70%.
-
What is 15 out of 60 as a percentage?
Using a calculator: 15 ÷ 60 × 100 = 25%.
These examples highlight the consistent application of the discussed methods across different numerical scenarios.
Beyond Basic Percentage Calculations: Advanced Applications
While this article focuses on basic percentage calculations, the underlying principles can be applied to more complex scenarios. These include:
-
Percentage increase and decrease: Calculating the percentage change between two values. This is frequently used to track growth or decline in various aspects of business, economics, and science. For example, calculating the percentage increase in sales revenue from one year to the next or the percentage decrease in unemployment rates.
-
Compound interest: Calculating interest on interest, a key concept in finance and investment. This involves iteratively calculating interest and adding it to the principal amount.
-
Percentage points: Distinguishing between percentage change and percentage points, which represent different measures of change and are often confused.
-
Weighted averages: Calculating averages where different values contribute differently to the overall average. This is common in grade calculation, where assignments might carry different weights.
Conclusion
Understanding how to calculate percentages is a crucial skill with wide-ranging practical applications. This article has demonstrated several methods for solving percentage problems, illustrated with examples and expanded upon their real-world relevance. By mastering these techniques, you’ll be better equipped to tackle various numerical challenges in your personal and professional life. Remember, whether you use the fraction method, the proportion method, or a calculator, the key is to understand the underlying principles of percentages and their significance in representing proportions and ratios. The ability to confidently calculate and interpret percentages is invaluable in navigating the quantitative aspects of everyday life and various professional fields.
Latest Posts
Latest Posts
-
Whats The Answer To A Division Problem Called
Apr 16, 2025
-
What Is Sublimation In The Water Cycle
Apr 16, 2025
-
In Celsius What Is The Freezing Point Of Water
Apr 16, 2025
-
52 In Is How Many Feet
Apr 16, 2025
-
Cuanto Son 10 Cm En Pulgadas
Apr 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 27 Out Of 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.