What Is 3/12 As A Percent
Kalali
Apr 13, 2025 · 6 min read
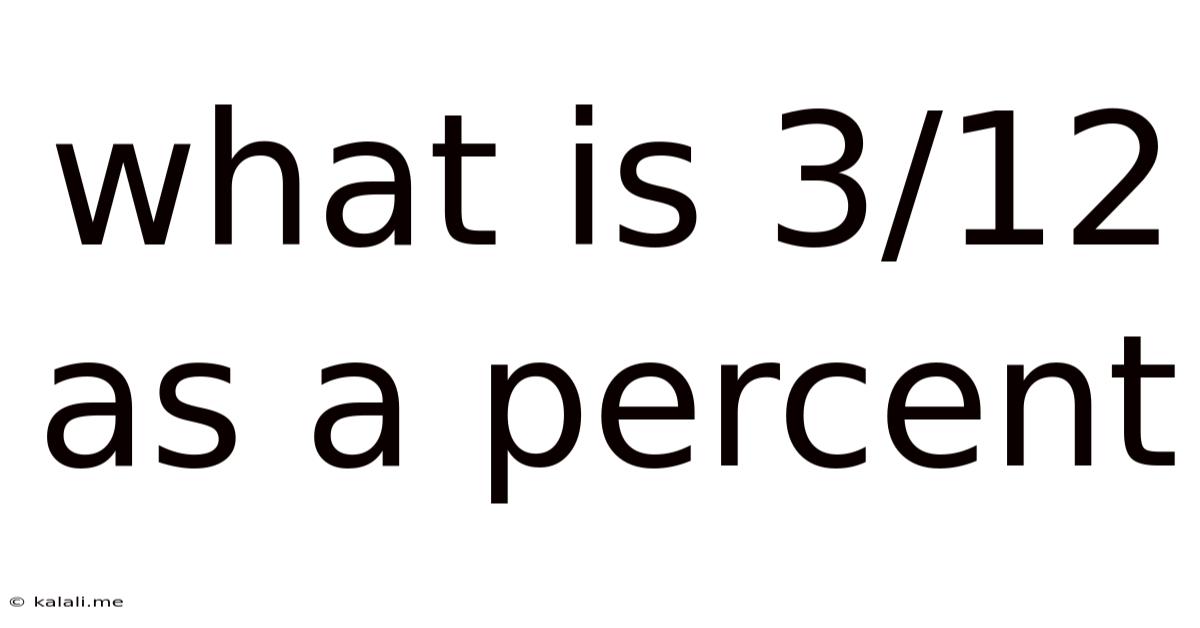
Table of Contents
What is 3/12 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with widespread applications in various fields, from finance and statistics to everyday life. This comprehensive guide delves into the process of converting the fraction 3/12 into a percentage, explaining the steps involved and providing a broader understanding of fraction-to-percentage conversion techniques. We'll also explore some practical examples and related concepts to solidify your grasp of this essential mathematical skill.
Meta Description: Learn how to convert the fraction 3/12 into a percentage. This detailed guide provides a step-by-step explanation, practical examples, and explores related concepts for a comprehensive understanding of fraction-to-percentage conversion.
Understanding Fractions and Percentages
Before we dive into converting 3/12, let's briefly review the concepts of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts in the whole.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, or 50/100.
The core relationship between fractions and percentages is that a percentage is simply a fraction with a denominator of 100. Therefore, converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100.
Converting 3/12 to a Percentage: Step-by-Step
Here's how to convert the fraction 3/12 to a percentage:
Step 1: Simplify the Fraction
The first step in converting 3/12 to a percentage is to simplify the fraction. Both the numerator (3) and the denominator (12) are divisible by 3. Dividing both by 3, we get:
3 ÷ 3 = 1 12 ÷ 3 = 4
So, 3/12 simplifies to 1/4. Simplifying fractions makes the conversion process easier and helps to avoid complex calculations. This step is crucial for efficient and accurate conversions. Always look for common factors between the numerator and denominator before proceeding.
Step 2: Convert the Simplified Fraction to a Decimal
To convert the simplified fraction 1/4 to a decimal, we divide the numerator (1) by the denominator (4):
1 ÷ 4 = 0.25
This gives us the decimal equivalent of the fraction. Decimal representation is an intermediate step frequently used in converting fractions to percentages. Mastering decimal division is therefore a key component of successful fraction-to-percentage conversions.
Step 3: Convert the Decimal to a Percentage
Finally, to convert the decimal 0.25 to a percentage, we multiply it by 100 and add the "%" symbol:
0.25 × 100 = 25%
Therefore, 3/12 is equal to 25%. This final step highlights the fundamental definition of a percentage: a fraction expressed as a part of 100. Multiplying by 100 effectively scales the decimal value to represent the equivalent proportion out of 100.
Alternative Method: Direct Conversion
While the step-by-step method is generally recommended for clarity, you can also convert directly from the original fraction to a percentage using a single calculation. This involves converting the fraction to a decimal, then multiplying by 100.
For 3/12:
3 ÷ 12 = 0.25 0.25 × 100 = 25%
This method is faster once you're comfortable with decimal division. However, simplifying the fraction first (as in the step-by-step method) often leads to simpler decimal calculations, reducing the risk of errors.
Practical Applications and Real-World Examples
Understanding fraction-to-percentage conversions is vital in many real-world situations:
-
Finance: Calculating interest rates, discounts, and profit margins often involves converting fractions to percentages. For instance, a 1/4 discount on a $100 item means a 25% discount, resulting in a price of $75.
-
Statistics: Percentages are frequently used to represent data proportions in surveys, polls, and research findings. For example, if 3 out of 12 respondents prefer a particular product, this represents a 25% preference rate.
-
Everyday Life: Calculating tips, expressing sale discounts, and understanding nutritional information often requires converting fractions to percentages for easier comprehension. For example, a recipe calling for 3/12 of a cup of sugar can be easily understood as 25% of a cup.
-
Test Scores: If a student answers 3 out of 12 questions correctly on a test, their score is 25%.
-
Measurement and Ratios: Many situations involving ratios and proportions in science, engineering, and construction require conversion between fractions and percentages for clear communication and analysis.
Further Exploration of Fraction-to-Percentage Conversions
This understanding extends to more complex fractions. The core principle remains the same: simplify the fraction (if possible), convert to a decimal by dividing the numerator by the denominator, and then multiply the decimal by 100 to obtain the percentage.
For instance:
- 5/20: Simplifies to 1/4, which is 0.25 or 25%
- 7/14: Simplifies to 1/2, which is 0.5 or 50%
- 15/60: Simplifies to 1/4, which is 0.25 or 25%
These examples demonstrate that different fractions can lead to the same percentage value, highlighting the importance of simplifying the fractions to their simplest form before calculation. This ensures efficient calculations and prevents potential errors associated with complex numbers. Focusing on simplifying fractions will become increasingly important as you tackle more intricate conversion problems.
Advanced Concepts and Applications
Beyond basic conversions, understanding fraction-to-percentage conversions unlocks more advanced mathematical concepts:
-
Ratio and Proportion: Fractions represent ratios, which are essential in solving various proportional problems. Converting these ratios to percentages allows for easy comparison and analysis.
-
Probability: Percentages are extensively used to express probabilities, allowing for a clear representation of the likelihood of certain events. Converting fractions representing probability to percentages provides a more intuitive understanding.
-
Data Analysis and Statistics: Percentages play a crucial role in interpreting statistical data and presenting findings in a clear and understandable manner.
-
Financial Modeling: Financial models rely heavily on percentage-based calculations for forecasting, risk assessment, and performance analysis.
Mastering fraction-to-percentage conversions builds a solid foundation for further mathematical exploration and applications in various quantitative fields.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a crucial skill with wide-ranging applications. By understanding the steps involved—simplifying the fraction, converting to a decimal, and then to a percentage—you equip yourself with a valuable tool for various mathematical and real-world scenarios. This guide provided a comprehensive approach, including alternative methods and practical examples, ensuring a thorough grasp of this fundamental mathematical concept. Remember that consistent practice and applying these principles to diverse examples will solidify your understanding and improve your accuracy in future calculations.
Latest Posts
Latest Posts
-
How Many Ml Is 2 L
Apr 15, 2025
-
What Are The Factors For 44
Apr 15, 2025
-
What Is One Percent Of One Billion
Apr 15, 2025
-
Inner Transition Metals In Periodic Table
Apr 15, 2025
-
How Many Inches In 500 Feet
Apr 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.