What Is 3 20 As A Percentage
Kalali
Mar 31, 2025 · 5 min read
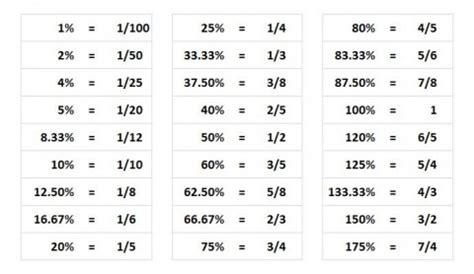
Table of Contents
What is 3/20 as a Percentage? A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will delve into the process of converting the fraction 3/20 into a percentage, explaining the steps involved and providing additional context to solidify your understanding. We'll explore various methods and show you how to tackle similar fraction-to-percentage conversions with ease.
Understanding Fractions and Percentages
Before we dive into the conversion, let's briefly review the concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, 3/20, 3 is the numerator and 20 is the denominator. This means we have 3 parts out of a total of 20 parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Method 1: The Direct Conversion Method
The most straightforward method to convert 3/20 to a percentage involves a two-step process:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
3 ÷ 20 = 0.15
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.15 x 100 = 15%
Therefore, 3/20 is equal to 15%.
Method 2: Using the Proportion Method
This method utilizes the concept of proportions to solve the problem. We set up a proportion where the fraction 3/20 is equal to an unknown percentage (x) out of 100:
3/20 = x/100
To solve for x, we can cross-multiply:
20x = 300
Then, divide both sides by 20:
x = 300 ÷ 20 = 15
Therefore, x = 15, meaning 3/20 is equal to 15%.
Method 3: Understanding the Relationship Between Fractions and Percentages
Another approach involves understanding the inherent relationship between fractions and percentages. Since a percentage is a fraction out of 100, we can manipulate the given fraction to have a denominator of 100.
To achieve this, we ask ourselves: what number, when multiplied by 20, gives us 100? The answer is 5. Therefore, we multiply both the numerator and the denominator of 3/20 by 5:
(3 x 5) / (20 x 5) = 15/100
Now, since 15/100 represents 15 out of 100, it's directly equivalent to 15%.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is crucial in many real-world scenarios:
-
Financial Calculations: Calculating interest rates, discounts, tax rates, and profit margins all involve percentage conversions. Understanding how to express fractions as percentages is essential for making informed financial decisions.
-
Data Analysis: Representing data in percentage form often makes it easier to understand and compare different proportions. For instance, expressing survey results or market shares as percentages offers a clear and concise representation.
-
Scientific Calculations: Many scientific calculations, particularly in fields like chemistry and biology, require converting fractions to percentages to express concentrations or proportions.
-
Everyday Life: From calculating tips in restaurants to understanding sale discounts in stores, converting fractions to percentages is a practical skill used daily.
Beyond 3/20: Converting Other Fractions to Percentages
The methods described above can be applied to convert any fraction to a percentage. Let's illustrate with a few examples:
-
Converting 1/4 to a percentage:
- Decimal conversion: 1 ÷ 4 = 0.25
- Percentage conversion: 0.25 x 100 = 25%
-
Converting 7/8 to a percentage:
- Decimal conversion: 7 ÷ 8 = 0.875
- Percentage conversion: 0.875 x 100 = 87.5%
-
Converting 5/6 to a percentage:
- Decimal conversion: 5 ÷ 6 ≈ 0.8333
- Percentage conversion: 0.8333 x 100 ≈ 83.33% (Note: This involves a recurring decimal, so we round it to two decimal places).
Dealing with Improper Fractions
Improper fractions (where the numerator is larger than the denominator) can also be converted to percentages using the same methods. For example:
Converting 7/4 to a percentage:
- Decimal conversion: 7 ÷ 4 = 1.75
- Percentage conversion: 1.75 x 100 = 175%
Note that percentages greater than 100% are perfectly valid and represent values exceeding the whole.
Mastering Percentage Conversions: Tips and Tricks
-
Practice Regularly: The key to mastering percentage conversions is consistent practice. Try converting various fractions to percentages to build your proficiency.
-
Use Calculators Strategically: While it’s important to understand the underlying principles, using a calculator can speed up the process, especially with complex fractions.
-
Memorize Common Equivalents: Familiarize yourself with the percentage equivalents of common fractions like 1/2 (50%), 1/4 (25%), 3/4 (75%), and 1/10 (10%). This will enhance your mental calculation abilities.
Conclusion
Converting 3/20 to a percentage is a simple yet essential mathematical skill. Through the various methods detailed above, we've demonstrated that 3/20 equals 15%. Understanding the process and applying it to different fractions will significantly improve your mathematical abilities and enhance your capacity to tackle real-world problems involving percentages. Remember to practice regularly to reinforce your understanding and build confidence in your calculations. The more you practice, the more natural and effortless this conversion process will become. Mastering this skill opens doors to a clearer understanding of numerical relationships and data analysis in many different contexts.
Latest Posts
Latest Posts
-
The Vibrations Of A Longitudinal Wave Move In A Direction
Apr 02, 2025
-
How Long Is 96 Inches In Feet
Apr 02, 2025
-
Common Multiples Of 16 And 24
Apr 02, 2025
-
How Many Ml Is 7 5 Oz
Apr 02, 2025
-
Lowest Common Multiple Of 8 And 9
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 20 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
