What Is 3 25 As A Percent
Kalali
Mar 19, 2025 · 5 min read
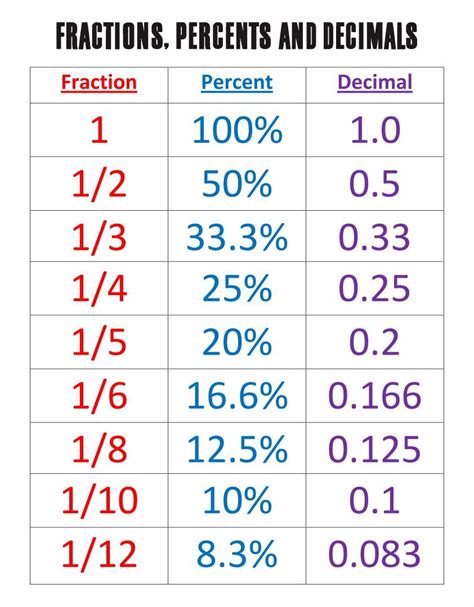
Table of Contents
What is 3/25 as a Percent? A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in various fields, from finance and statistics to everyday life. Understanding this process empowers you to easily interpret data, compare proportions, and solve problems involving ratios and proportions. This comprehensive guide will delve into the conversion of the fraction 3/25 to a percentage, explaining the process step-by-step and exploring the underlying mathematical principles. We'll also examine different methods for solving similar problems, equipping you with the tools to confidently tackle any fraction-to-percentage conversion.
Understanding Fractions and Percentages
Before we jump into the conversion, let's briefly recap the concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It is expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of parts the whole is divided into. For example, in the fraction 3/25, 3 is the numerator and 25 is the denominator. This means we have 3 parts out of a total of 25 parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Percentages are often denoted by the symbol "%". For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 3/25 to a Percentage: The Step-by-Step Method
The conversion of a fraction to a percentage involves two main steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In our case:
3 ÷ 25 = 0.12
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol. Therefore:
0.12 x 100 = 12%
Therefore, 3/25 is equal to 12%.
Alternative Methods for Conversion
While the above method is the most straightforward, several other approaches can be used to convert fractions to percentages.
Method 1: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. Since percentages are based on 100, this directly gives us the percentage. To do this, we need to determine what number we multiply the denominator (25) by to get 100.
25 x 4 = 100
We must then multiply the numerator (3) by the same number (4):
3 x 4 = 12
This gives us the equivalent fraction 12/100, which is equal to 12%.
Method 2: Using Proportions
This method uses the concept of proportions to solve for the percentage. We can set up a proportion:
3/25 = x/100
To solve for x (the percentage), we can cross-multiply:
25x = 300
x = 300 ÷ 25
x = 12
Therefore, x = 12%, confirming our previous result.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is crucial in many real-world scenarios. Here are a few examples:
-
Calculating Discounts: If a store offers a 20% discount on an item, you can easily calculate the discount amount by converting the percentage to a fraction (20/100 = 1/5) and multiplying it by the original price.
-
Analyzing Test Scores: If you scored 18 out of 25 on a test, converting 18/25 to a percentage (72%) provides a clearer understanding of your performance.
-
Understanding Financial Statements: Financial reports often use percentages to represent key ratios and proportions, such as profit margins, debt-to-equity ratios, and return on investment. Understanding these percentages requires the ability to convert fractions to percentages.
-
Interpreting Statistical Data: Many statistical analyses involve working with proportions and probabilities, often expressed as fractions. Converting these fractions to percentages allows for easier interpretation and comparison.
Expanding on the Concept: Working with More Complex Fractions
The methods discussed above can be applied to more complex fractions as well. For example, let's consider the fraction 17/68.
Step 1: Simplify the fraction (if possible).
In this case, both the numerator and the denominator are divisible by 17:
17 ÷ 17 = 1 68 ÷ 17 = 4
The simplified fraction is 1/4.
Step 2: Convert the simplified fraction to a decimal.
1 ÷ 4 = 0.25
Step 3: Convert the decimal to a percentage.
0.25 x 100 = 25%
Therefore, 17/68 is equal to 25%.
Troubleshooting Common Mistakes
When converting fractions to percentages, some common mistakes can occur:
-
Incorrect Division: Ensure you correctly divide the numerator by the denominator when converting the fraction to a decimal. Using a calculator can help avoid errors.
-
Forgetting to Multiply by 100: Remember to multiply the decimal by 100 to obtain the percentage. Omitting this step leads to an incorrect result.
-
Improper Simplification: Always simplify the fraction before converting it to a decimal if possible. This simplifies the calculation and minimizes the risk of errors.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill with widespread applications. By understanding the different methods and avoiding common mistakes, you can confidently perform these conversions and apply them to various real-world situations. This guide provides a comprehensive understanding of the process, empowering you to handle any fraction-to-percentage conversion with ease and accuracy. Remember to practice regularly to solidify your understanding and improve your speed and efficiency. Mastering this skill will enhance your analytical abilities and broaden your problem-solving capabilities in numerous contexts.
Latest Posts
Latest Posts
-
What Is The Decimal Of 75
May 09, 2025
-
What Percent Of 5 Is 4
May 09, 2025
-
What Type Of Symmetry Do Sea Stars Have
May 09, 2025
-
How Many Oz Are In 12 Cups
May 09, 2025
-
Cuanto Es 160 Centimetros En Pulgadas
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.