What Is 3 4 Divided By 1 4
Kalali
Jul 22, 2025 · 5 min read
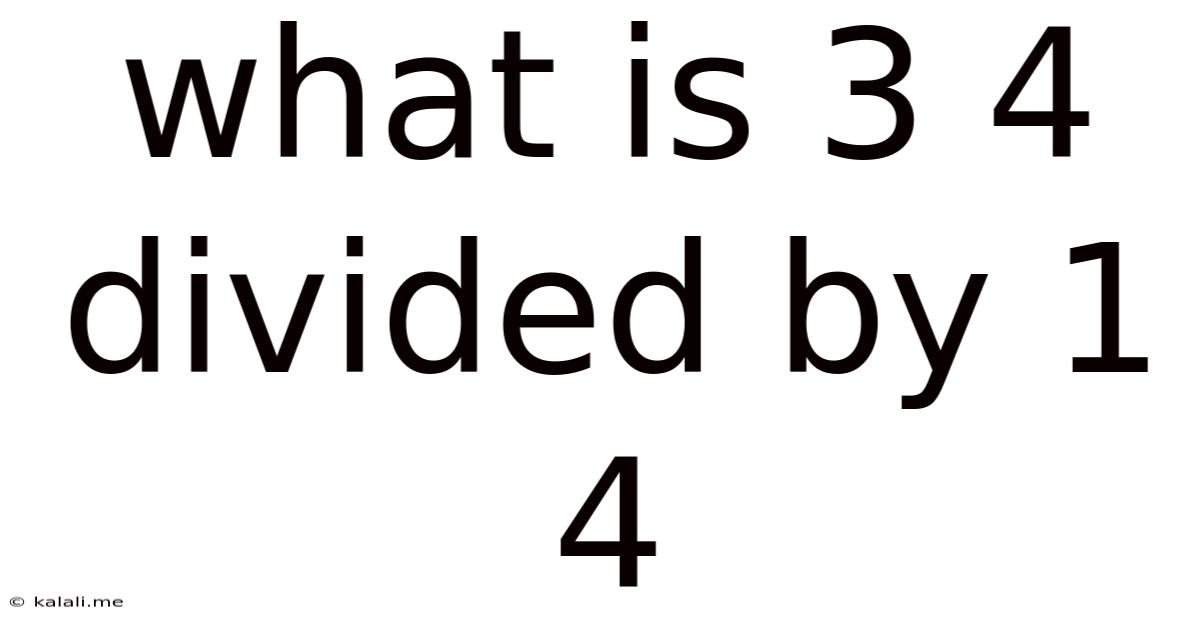
Table of Contents
What is 3/4 Divided by 1/4? A Deep Dive into Fraction Division
This seemingly simple question, "What is 3/4 divided by 1/4?", actually opens the door to a deeper understanding of fraction division, a fundamental concept in mathematics with broad applications in various fields. This article will not only answer the question directly but also explore the underlying principles, provide multiple methods for solving similar problems, and discuss the practical relevance of fraction division in everyday life and advanced studies.
Understanding Fractions: A Quick Refresher
Before diving into division, let's revisit the basics of fractions. A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3 and the denominator is 4, meaning we have 3 out of 4 equal parts of a whole.
Method 1: The "Keep, Change, Flip" Method
This is arguably the most popular method for dividing fractions. It's simple, efficient, and easy to remember:
- Keep the first fraction (the dividend) exactly as it is: 3/4
- Change the division sign (÷) to a multiplication sign (×).
- Flip the second fraction (the divisor) – this means inverting the numerator and denominator: 1/4 becomes 4/1.
Now, you have a multiplication problem: (3/4) × (4/1). Multiply the numerators together and the denominators together:
(3 × 4) / (4 × 1) = 12/4
Finally, simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4 in this case:
12/4 = 3
Therefore, 3/4 divided by 1/4 equals 3.
Method 2: Using the Reciprocal
This method is essentially the same as the "Keep, Change, Flip" method, but it emphasizes the concept of the reciprocal. The reciprocal of a fraction is obtained by swapping its numerator and denominator. The reciprocal of 1/4 is 4/1. Dividing by a fraction is equivalent to multiplying by its reciprocal.
So, 3/4 ÷ 1/4 = 3/4 × 4/1 = 12/4 = 3
Method 3: Visual Representation
Visualizing the problem can be helpful, especially for beginners. Imagine you have a pizza cut into 4 equal slices. You have 3 of these slices (3/4 of the pizza). Now, you want to divide this 3/4 pizza into portions that are each 1/4 of the pizza. How many 1/4 slices can you get from your 3/4 pizza? You can clearly see you can get three 1/4 slices.
Method 4: Converting to Decimal (Less Recommended for this example)
While you can convert fractions to decimals before dividing, it's generally less efficient and can lead to rounding errors, especially with fractions that don't produce terminating decimals. In this case, however, it's straightforward:
3/4 = 0.75 1/4 = 0.25
0.75 ÷ 0.25 = 3
Although this works here, this approach isn't always as clean or accurate as the fraction methods.
Why Understanding Fraction Division is Important
The ability to divide fractions is crucial in many areas, including:
-
Cooking and Baking: Scaling recipes up or down requires understanding how to divide fractional measurements. If a recipe calls for 1/2 cup of flour and you want to make half the recipe, you need to divide 1/2 by 2 (or multiply by 1/2).
-
Sewing and Crafting: Many sewing and crafting projects involve working with fractional measurements of fabric, yarn, or other materials.
-
Construction and Engineering: Precision in construction and engineering depends on accurate calculations involving fractions and fraction division. Calculating the length of materials or proportions in blueprints often requires dividing fractions.
-
Finance and Accounting: Calculating percentages, proportions, and shares often involves working with fractions and fraction division.
-
Data Analysis and Statistics: Many statistical calculations rely on working with fractions and ratios, necessitating a firm grasp of fraction division.
-
Higher-Level Mathematics: Fraction division forms the foundation for more advanced mathematical concepts like algebra, calculus, and linear algebra.
Solving More Complex Fraction Division Problems
The methods described above can be applied to more complex fraction division problems. For example, let's consider 5/6 divided by 2/3:
- Keep, Change, Flip: (5/6) × (3/2) = 15/12
- Simplify: 15/12 = 5/4 or 1 1/4
Mixed Numbers and Fraction Division
When dealing with mixed numbers (a whole number and a fraction, like 1 1/2), convert them to improper fractions before applying the division methods. For example, to divide 1 1/2 by 1/4:
- Convert to improper fraction: 1 1/2 = 3/2
- Apply the "Keep, Change, Flip" method: (3/2) × (4/1) = 12/2 = 6
Conclusion:
The answer to "What is 3/4 divided by 1/4?" is unequivocally 3. However, the real value lies not just in the answer itself, but in understanding the underlying principles of fraction division and the various methods for solving these types of problems. Mastering fraction division is a fundamental skill with wide-ranging applications across numerous disciplines. By understanding these methods and practicing regularly, you'll build a strong foundation for more advanced mathematical concepts and real-world problem-solving. Remember to always simplify your final answer to its lowest terms.
Latest Posts
Latest Posts
-
Abandon Hope All Ye Who Enter Here In Latin
Jul 23, 2025
-
Closest Ocean Beach To Louisville Ky From My Location
Jul 23, 2025
-
How Many 1 5 Oz Shots In A Liter
Jul 23, 2025
-
Which Story Element Most Clearly Shows Direct Characterization
Jul 23, 2025
-
What Is The Gcf For 15 And 20
Jul 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 4 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.