What Is 3 4 Of 1 4
Kalali
Jul 27, 2025 · 6 min read
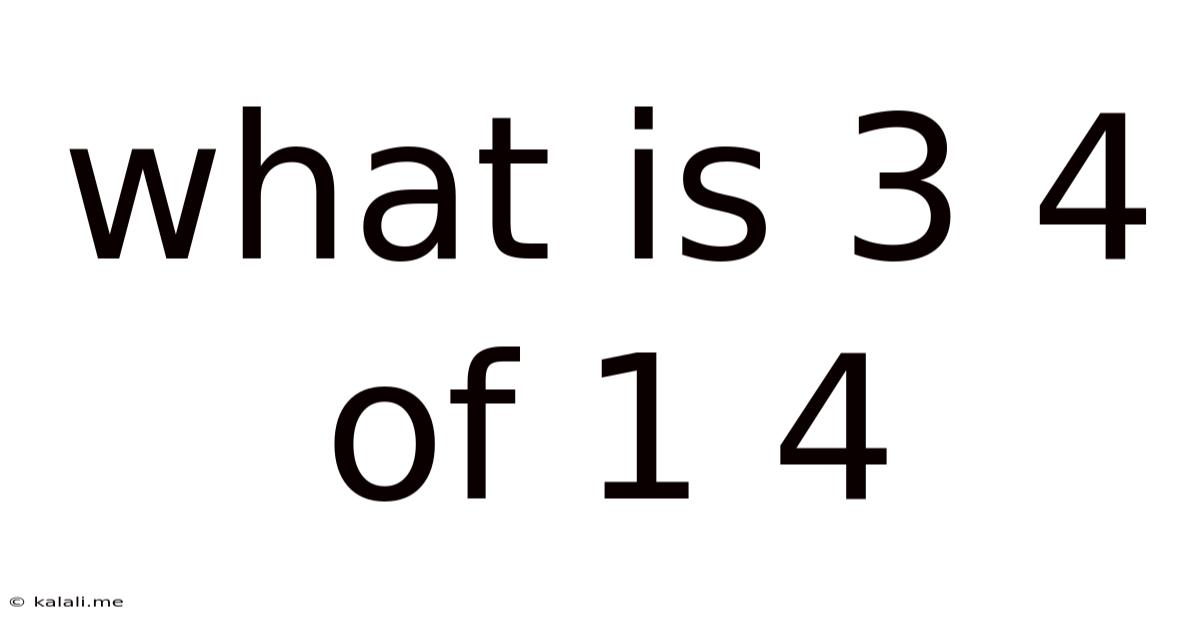
Table of Contents
What is ¾ of ¼? Unraveling Fractions and Their Applications
This seemingly simple question, "What is ¾ of ¼?", opens a door to a deeper understanding of fractions, their manipulation, and their practical applications in various fields. While the calculation itself is straightforward, exploring the underlying concepts provides a solid foundation for more complex mathematical problems. This article will not only answer the question but also delve into the methodologies, provide real-world examples, and explore the broader significance of fractional calculations.
Meta Description: Discover the answer to "What is ¾ of ¼?" and explore the world of fractions, including multiplication, simplification, and real-world applications in various fields like cooking, construction, and data analysis. Learn how to confidently tackle fractional calculations and understand their importance.
Understanding Fractions: A Refresher
Before we dive into the calculation, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we're considering.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction ½, the numerator (1) represents one part, and the denominator (2) represents that the whole is divided into two equal parts.
Calculating ¾ of ¼: The Method
To find ¾ of ¼, we perform a multiplication operation. The word "of" in this context signifies multiplication. Therefore, the calculation is:
(¾) * (¼)
Multiplying fractions involves multiplying the numerators together and the denominators together:
(3 * 1) / (4 * 4) = 3/16
Therefore, ¾ of ¼ is 3/16.
Simplifying Fractions: A Crucial Step
While 3/16 is the correct answer, it's always good practice to check if the resulting fraction can be simplified. A fraction is simplified when the numerator and denominator have no common factors other than 1. In this case, 3 and 16 have no common factors, so the fraction 3/16 is already in its simplest form.
Visualizing Fractions: A Geometric Approach
Understanding fractions becomes easier with visualization. Imagine a square representing the whole (1). To represent ¼, divide the square into four equal parts and shade one part. Now, to find ¾ of this ¼, take three-quarters of the already shaded area. This would involve dividing the shaded quarter into three equal parts and then selecting two of them. In total, 3 out of 16 parts of the original square would be selected, which visually confirms that ¾ of ¼ is 3/16.
Real-World Applications of Fractional Calculations
Fractional calculations are far from theoretical exercises. They find practical applications in numerous areas:
- Cooking and Baking: Recipes often involve fractions. For example, a recipe might call for ¾ cup of flour and ¼ cup of sugar. Understanding fractional calculations is crucial for accurate measurement and consistent results.
- Construction and Engineering: Precision is paramount in construction. Calculations involving fractions are commonplace when measuring materials, determining angles, and ensuring structural integrity. Understanding fractional measurements ensures accuracy in building and designing structures.
- Finance and Investments: Fractions are frequently used in financial calculations. Interest rates, stock prices, and profit margins are often expressed as fractions or percentages (which are simply fractions expressed as parts of 100).
- Data Analysis and Statistics: In statistics and data analysis, fractions and ratios are essential for representing proportions and percentages within datasets. Understanding how to manipulate these fractions is crucial for data interpretation and decision-making.
- Sewing and Tailoring: Pattern making and garment construction often require precise measurements, many of which are expressed as fractions of an inch. Accurate fractional calculations are essential for achieving the desired fit and finish of a garment.
- Mapping and Surveying: Accurate land surveying and mapmaking relies on fractional calculations for determining precise distances and areas. This ensures accurate representation of land parcels and geographic features.
Extending the Concept: More Complex Fractional Calculations
The principles used to solve ¾ of ¼ can be extended to more complex scenarios involving the multiplication of multiple fractions or a combination of multiplication and other operations. For instance, calculating (2/3) * (5/7) * (1/2) involves multiplying the numerators and denominators together, simplifying if possible. This results in (10/42), which simplifies to (5/21). The same fundamental principles remain.
Moreover, solving problems involving mixed numbers (numbers with a whole number and a fractional part) requires converting the mixed numbers into improper fractions (where the numerator is larger than the denominator) before performing multiplication. For example, to calculate 1 ½ multiplied by 2/3, you'd first convert 1 ½ to 3/2 and then multiply it by 2/3 resulting in 6/6 which simplifies to 1.
Converting Fractions to Decimals and Percentages
While fractions are a powerful way to represent parts of a whole, decimals and percentages offer alternative representations with their own advantages. Converting a fraction to a decimal involves dividing the numerator by the denominator. For example, 3/16 = 0.1875. Converting a fraction to a percentage involves multiplying the decimal equivalent by 100%. Therefore, 3/16 = 18.75%. Each representation has its own utility depending on the context. Decimals are often used for more precise calculations, while percentages provide an easily understandable representation of proportions.
Understanding the inter-conversion between these representations enhances our ability to handle mathematical problems in various forms. It also allows us to compare and contrast results obtained through different calculation methods.
Addressing Common Mistakes in Fractional Calculations
Several common mistakes can occur when working with fractions:
- Incorrect Multiplication: Failing to multiply both the numerators and the denominators separately is a frequent error. Remember, multiplying fractions involves multiplying the numerators and then multiplying the denominators.
- Simplification Errors: Not simplifying the fraction to its lowest terms can lead to inaccurate or cumbersome results. Always check for common factors between the numerator and denominator.
- Improper Fraction Conversion: Incorrectly converting mixed numbers to improper fractions can significantly impact the accuracy of calculations. Make sure to review the process of conversion to ensure accuracy.
- Incorrect Order of Operations: If a problem involves multiple operations (addition, subtraction, multiplication, and division), remember the order of operations (PEMDAS/BODMAS) to ensure correct calculations.
Conclusion: Mastering Fractions for Real-World Success
The seemingly simple question, "What is ¾ of ¼?", serves as a springboard to explore the world of fractions, their calculations, and their wide-ranging applications. Mastering fractional calculations is not merely an academic exercise; it's a crucial skill with practical implications in diverse fields. By understanding the underlying concepts, mastering the techniques, and recognizing common pitfalls, you can confidently tackle fractional calculations and leverage this knowledge for success in your chosen field, whether it's cooking, construction, finance, or any other area that requires precise measurement and calculation. The ability to confidently manipulate fractions empowers you to approach complex problems with precision and accuracy, ultimately leading to more informed and effective decision-making. So, next time you encounter a fractional calculation, remember the fundamental principles, visualize the process, and approach it with confidence. You've got this!
Latest Posts
Latest Posts
-
How Much Was A Gallon Of Milk In 1902
Jul 27, 2025
-
Math Words That Start With J 8th Grade
Jul 27, 2025
-
100 Square Meters Is How Many Square Feet
Jul 27, 2025
-
How Many Ounces Is In 6 Pounds
Jul 27, 2025
-
How Many Feet Are In 3 4 Of An Acre
Jul 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 4 Of 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.