What Is 3 Divided By 3 4
Kalali
Aug 21, 2025 · 5 min read
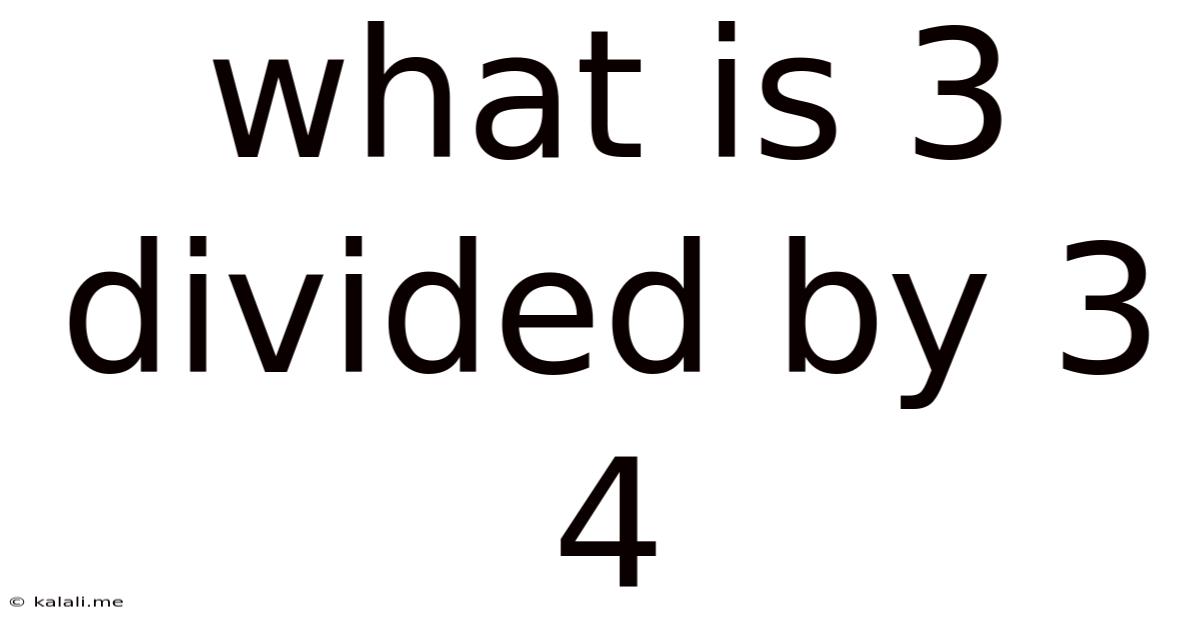
Table of Contents
What is 3 Divided by 3/4? Understanding Fraction Division
This seemingly simple question, "What is 3 divided by 3/4?", often trips up students and even adults who haven't practiced fraction arithmetic in a while. It highlights a crucial concept in mathematics: fraction division. This article will comprehensively explain how to solve this problem, delve into the underlying principles of fraction division, and explore various methods to tackle similar problems. By the end, you'll not only understand the answer but also gain confidence in tackling more complex fraction operations.
Meta Description: Learn how to divide whole numbers by fractions! This comprehensive guide explains how to solve 3 divided by 3/4, explores different methods, and provides practical examples for mastering fraction division.
Understanding the Problem: 3 ÷ 3/4
The problem, 3 ÷ 3/4, asks us to determine how many times the fraction 3/4 fits into the whole number 3. We're essentially splitting the whole number 3 into groups of 3/4. Think of it like sharing 3 pizzas among friends, where each friend gets 3/4 of a pizza. How many friends can you feed? This real-world analogy helps visualize the division process.
Method 1: The "Keep, Change, Flip" Method (or Invert and Multiply)
This is the most common and arguably the easiest method for dividing fractions. It involves three simple steps:
- Keep: Keep the first number (the dividend) as it is. In this case, we keep the 3.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second number (the divisor) – which is the fraction – upside down. This means we find the reciprocal of 3/4, which is 4/3.
So, our problem transforms from 3 ÷ 3/4 to 3 × 4/3.
Now, we simply multiply the numbers:
3 × 4/3 = (3 × 4) / 3 = 12 / 3 = 4
Therefore, 3 divided by 3/4 is 4.
Method 2: Converting to Improper Fractions
This method involves converting the whole number into a fraction before performing the division. Remember that any whole number can be written as a fraction with a denominator of 1. In this case, 3 can be written as 3/1.
Now, our problem becomes: (3/1) ÷ (3/4).
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction:
(3/1) × (4/3) = (3 × 4) / (1 × 3) = 12 / 3 = 4
Again, the answer is 4.
Method 3: Visual Representation
While less efficient for complex problems, visualizing the division can provide a strong intuitive understanding. Imagine three whole circles representing the number 3. We want to divide these circles into portions of 3/4.
- Take the first circle and divide it into four equal quarters. Three of these quarters represent 3/4.
- Repeat this process for the second circle. Again, you get another 3/4.
- Repeat again for the third circle, getting a third 3/4.
- You've now used all three circles, and you have created exactly four groups of 3/4.
This visual representation clearly demonstrates that 3 divided by 3/4 equals 4.
Why Does "Keep, Change, Flip" Work?
The "Keep, Change, Flip" method isn't just a trick; it's a consequence of the mathematical definition of division. Dividing by a fraction is the same as multiplying by its reciprocal. Let's explore this further:
Consider the general case of a/b ÷ c/d. Division is defined as the inverse of multiplication. Therefore, a/b ÷ c/d is the number x such that (c/d) * x = a/b.
To solve for x, we multiply both sides by d/c (the reciprocal of c/d):
(d/c) * (c/d) * x = (d/c) * (a/b)
Since (d/c) * (c/d) = 1, we are left with:
x = (d/c) * (a/b)
This demonstrates that dividing by a fraction is equivalent to multiplying by its reciprocal – the mathematical basis for the "Keep, Change, Flip" method.
Applying the Concepts to More Complex Problems
Let's try some more examples to solidify our understanding:
Example 1: 5 ÷ 2/3
Using the "Keep, Change, Flip" method:
5 ÷ 2/3 = 5 × 3/2 = 15/2 = 7.5
Example 2: 7/8 ÷ 1/4
Using the "Keep, Change, Flip" method:
7/8 ÷ 1/4 = 7/8 × 4/1 = 28/8 = 7/2 = 3.5
Example 3: 2 1/2 ÷ 1/4
First, convert the mixed number to an improper fraction: 2 1/2 = 5/2
Then apply the "Keep, Change, Flip" method:
5/2 ÷ 1/4 = 5/2 × 4/1 = 20/2 = 10
Common Mistakes to Avoid
- Forgetting to flip the fraction: This is the most common error. Remember that you are finding the reciprocal of the divisor.
- Incorrect multiplication of fractions: Ensure you multiply numerators together and denominators together.
- Not simplifying the answer: Always simplify your answer to its lowest terms if possible.
- Mixing up the order: Remember that the order matters in division. a ÷ b is not the same as b ÷ a.
Conclusion: Mastering Fraction Division
Mastering fraction division is fundamental to a strong grasp of arithmetic. The "Keep, Change, Flip" method provides a straightforward and efficient way to solve these problems. Understanding the underlying mathematical principles reinforces the method and allows you to confidently tackle more complex fraction operations in algebra and beyond. By practicing regularly and using visual aids when necessary, you can confidently conquer the world of fraction division. Remember the key steps: keep, change, flip, and then simplify your answer. Practice with a variety of problems to solidify your understanding and build your skills. Don't hesitate to revisit the different methods outlined here to reinforce your learning. With consistent practice, you'll become a fraction division expert in no time!
Latest Posts
Latest Posts
-
How To Get To 26 Federal Plaza By Train
Aug 21, 2025
-
How Do You Say Jeremy In Spanish
Aug 21, 2025
-
The Speed Limit For Passenger Cars In Urban Districts Is
Aug 21, 2025
-
Postal Code Of Gulistan E Jauhar Karachi Pakistan
Aug 21, 2025
-
Why Did Sam Let Dean Turn Into A Vampire
Aug 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.