What Is 3 Out Of 7 As A Percentage
Kalali
Apr 17, 2025 · 5 min read
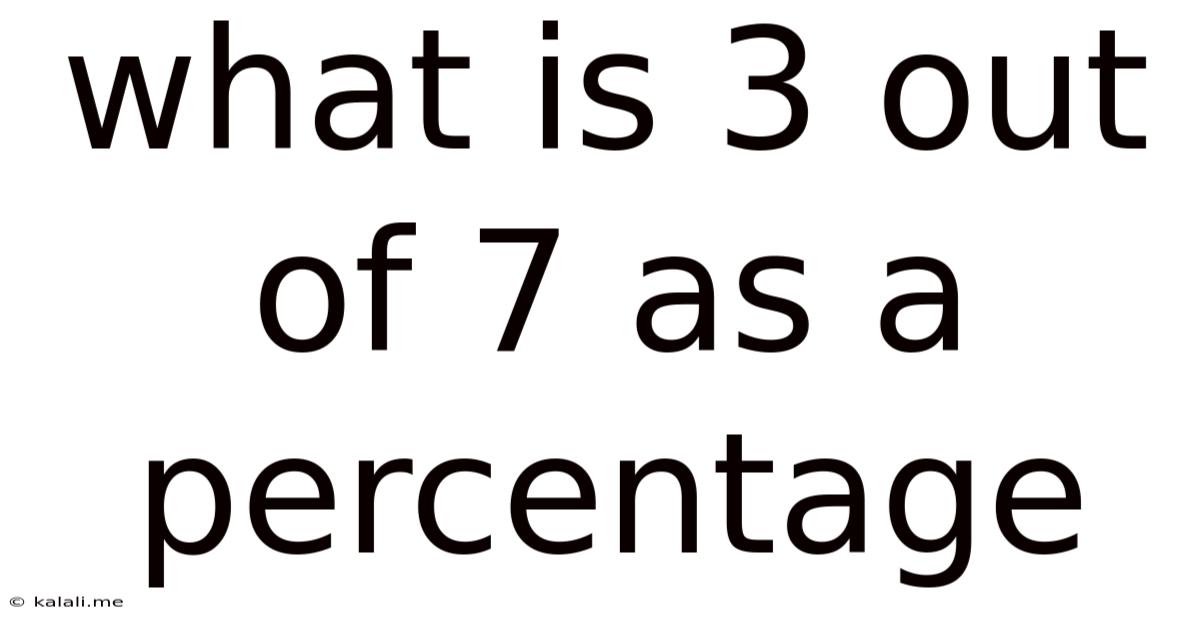
Table of Contents
What is 3 out of 7 as a Percentage? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to understanding statistics and financial reports. This article delves into the question: "What is 3 out of 7 as a percentage?" We'll not only provide the answer but also explore the underlying principles of percentage calculations, different methods to solve the problem, and real-world applications. This guide aims to equip you with the knowledge and tools to tackle similar percentage problems confidently.
Meta Description: Learn how to calculate percentages easily! This comprehensive guide explains how to determine what 3 out of 7 represents as a percentage, covering various methods and real-world applications. Master percentage calculations today!
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum in Latin). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Percentages are used extensively because they provide a standardized way to compare proportions and ratios.
Method 1: The Direct Conversion Method
This method involves directly converting the fraction 3/7 into a percentage. Here's how:
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (7). 3 ÷ 7 ≈ 0.42857
-
Multiply the decimal by 100: This converts the decimal to a percentage. 0.42857 × 100 ≈ 42.857%
-
Round to the desired precision: Depending on the context, you might round the percentage to a specific number of decimal places. For example, rounding to two decimal places gives us 42.86%.
Therefore, 3 out of 7 is approximately 42.86%.
Method 2: Using Proportions
This method uses the concept of proportions to solve the problem. We can set up a proportion to find the percentage:
3/7 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
7x = 300
x = 300/7
x ≈ 42.86
Therefore, using proportions, we again find that 3 out of 7 is approximately 42.86%.
Method 3: Utilizing a Calculator
Most calculators have a percentage function that simplifies the calculation. Simply divide 3 by 7 and then multiply the result by 100. The calculator will directly provide the percentage value. This is the quickest method for obtaining the answer, particularly for more complex calculations.
Real-World Applications: Examples of Percentage Calculations
Understanding percentage calculations is crucial in many everyday situations. Let's explore a few examples:
-
Discounts: A store offers a 20% discount on an item priced at $50. The discount amount is 20% of $50, which is (20/100) * $50 = $10. The final price is $50 - $10 = $40.
-
Taxes: A sales tax of 6% is applied to a purchase of $100. The tax amount is 6% of $100, which is (6/100) * $100 = $6. The total cost including tax is $100 + $6 = $106.
-
Grades and Scores: If a student answers 15 out of 20 questions correctly on a test, their score is (15/20) * 100 = 75%.
-
Financial Investments: Calculating the return on investment (ROI) often involves percentages. For instance, if an investment of $1,000 yields a profit of $150, the ROI is (150/1000) * 100 = 15%.
-
Data Analysis: Percentages are frequently used in data analysis to represent proportions and trends within datasets. For example, if a survey shows that 30% of respondents prefer a particular product, this indicates a significant preference.
Beyond the Basics: Working with More Complex Percentages
While the example of 3 out of 7 is relatively straightforward, the principles can be applied to more complex scenarios. Consider these extensions:
-
Finding the original value: If you know a percentage and the resulting value, you can work backward to find the original value. For example, if 20% of a number is 10, the original number is 10/(20/100) = 50.
-
Percentage increase or decrease: Calculating percentage changes is common in various fields. For example, if a quantity increases from 100 to 120, the percentage increase is [(120-100)/100] * 100 = 20%.
-
Compound percentages: In situations involving multiple percentage changes, the order of operations matters. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Percentage points: It's important to distinguish between percentage points and percentages. A change from 10% to 20% is a 10 percentage point increase, but a 100% increase in the percentage itself.
Troubleshooting Common Errors in Percentage Calculations
Several common errors can occur when calculating percentages. Being aware of these potential pitfalls can help you avoid mistakes:
-
Incorrect order of operations: Ensure you follow the correct order of operations (PEMDAS/BODMAS) when performing calculations involving multiple steps.
-
Mixing percentages and decimal values: Avoid mixing percentages and decimal values without proper conversion. Always ensure consistent units throughout your calculations.
-
Rounding errors: Rounding too early in the calculation can lead to inaccuracies in the final result. Round only at the end of the calculation to minimize errors.
-
Incorrect interpretation of percentage change: Carefully distinguish between percentage points and percentage changes when dealing with percentage increases or decreases.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages is a valuable skill that extends far beyond simple arithmetic. From everyday financial transactions to complex statistical analysis, the ability to work confidently with percentages is essential for navigating the numerical world. This comprehensive guide has provided various methods for solving the problem "What is 3 out of 7 as a percentage?" and has also explored the broader context of percentage calculations, equipping you with the knowledge and tools to approach similar problems with increased confidence and accuracy. Remember to practice regularly to solidify your understanding and to identify and avoid common errors. The more you practice, the more natural and intuitive percentage calculations will become.
Latest Posts
Latest Posts
-
What Is 5 7 As A Decimal
Apr 19, 2025
-
20 Of What Number Is 16
Apr 19, 2025
-
How Long Is 75cm In Inches
Apr 19, 2025
-
Cuanto Es 30 Pulgadas En Metros
Apr 19, 2025
-
Cuanto Es 50 Yardas En Metros
Apr 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Out Of 7 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.