What Is 3 Percent Of 10000
Kalali
Apr 19, 2025 · 5 min read
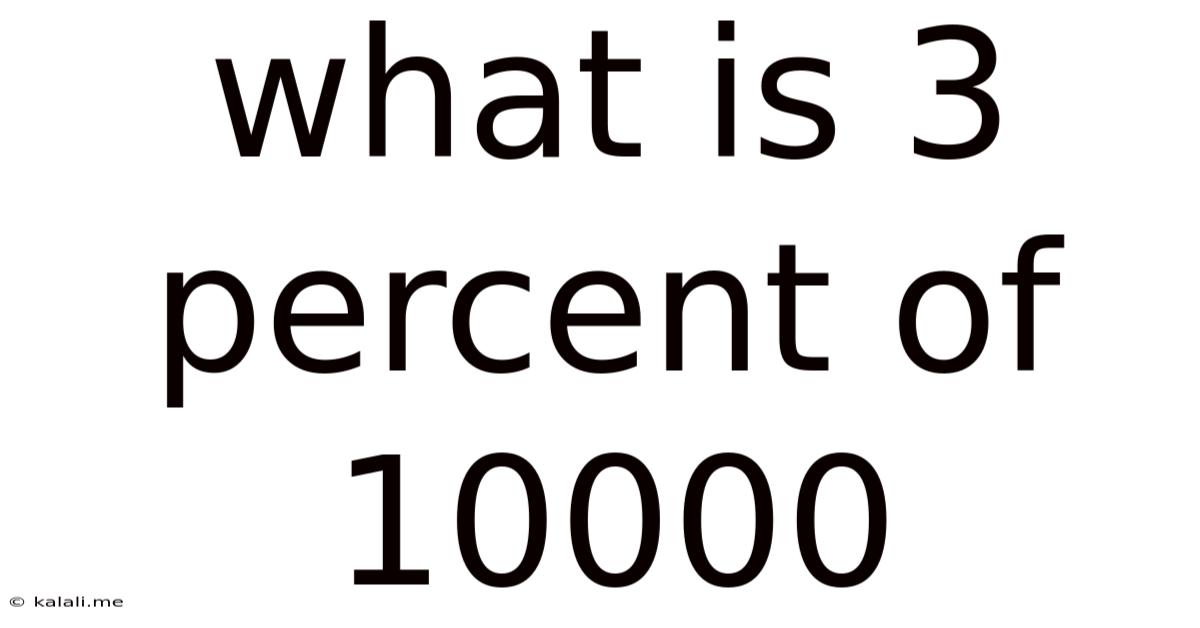
Table of Contents
What is 3 Percent of 10000? A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex financial analyses and scientific research. This article delves into the seemingly simple question, "What is 3 percent of 10000?", providing not just the answer but a comprehensive understanding of the underlying concepts, different calculation methods, and real-world examples to solidify your grasp of percentages. Understanding this seemingly basic calculation unlocks a broader understanding of proportional reasoning and its significance.
Meta Description: This comprehensive guide explains how to calculate 3% of 10000, covering various methods, real-world examples, and the importance of percentage calculations in different fields. Learn about percentage applications and improve your mathematical skills.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. Essentially, it represents a portion of a whole. The whole is often considered as 100%, and any part of that whole is expressed as a percentage relative to the 100%. For example, 50% means 50 out of 100, or half.
Calculating 3% of 10000: Three Methods
There are several ways to calculate 3% of 10000. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. First, convert the percentage to its decimal equivalent by dividing by 100. 3% becomes 0.03 (3 divided by 100). Then, multiply this decimal by the whole number (10000).
0.03 * 10000 = 300
Therefore, 3% of 10000 is 300.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 3% is equivalent to 3/100. To find 3% of 10000, multiply the fraction by 10000:
(3/100) * 10000 = 300
Again, the answer is 300. This method highlights the relationship between percentages, fractions, and decimals.
Method 3: Proportion Method
This method uses proportions to solve the problem. We can set up a proportion:
3/100 = x/10000
To solve for x (which represents 3% of 10000), cross-multiply:
100x = 3 * 10000 100x = 30000 x = 30000 / 100 x = 300
This confirms, once more, that 3% of 10000 is 300.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-life situations. Here are a few examples:
-
Finance: Calculating interest on loans, savings accounts, and investments heavily relies on percentages. Understanding interest rates and compound interest requires a solid grasp of percentage calculations. For example, calculating the interest earned on a $10,000 investment with a 3% annual interest rate would directly use this calculation.
-
Sales and Discounts: Retail stores frequently advertise discounts as percentages. If a $10,000 car has a 3% discount, you would save $300. This simple percentage calculation helps consumers make informed purchasing decisions.
-
Taxes: Sales tax, income tax, and property tax are usually expressed as percentages of the taxable amount. Understanding these percentages is vital for budgeting and financial planning.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting data. For example, expressing survey results or population demographics often involves percentages. Calculating the percentage change between two values is also common in data analysis.
-
Science and Engineering: Percentages are used in various scientific and engineering calculations, such as calculating efficiency, error margins, and concentration levels. For example, in chemistry, expressing the concentration of a solution is often done using percentage.
-
Everyday Budgeting: Tracking spending, saving goals, and managing personal finances often involve percentage calculations. For instance, determining the percentage of income allocated to different expenses (housing, food, transportation, etc.) improves financial management.
Expanding on Percentage Calculations: More Complex Scenarios
While calculating 3% of 10000 is relatively straightforward, understanding percentage calculations extends to more complex scenarios:
-
Calculating Percentage Increase or Decrease: This involves finding the percentage change between two values. The formula is: [(New Value - Old Value) / Old Value] * 100%. This is useful when comparing changes over time, such as population growth or stock prices.
-
Finding the Original Value: If you know the percentage and the resulting value, you can work backward to find the original value. This might be necessary when dealing with discounted prices or after-tax amounts.
-
Compounding Percentages: This involves calculating percentages repeatedly, such as in compound interest calculations. Compound interest is interest earned on both the principal amount and accumulated interest.
-
Working with Multiple Percentages: Sometimes, you might need to apply multiple percentages sequentially, such as calculating discounts and taxes together.
Tips and Tricks for Calculating Percentages
-
Use a Calculator: For larger numbers or more complex calculations, a calculator is a useful tool. Many calculators have a dedicated percentage function.
-
Master the Decimal Conversion: Understanding how to convert percentages to decimals and vice versa is crucial for efficient calculation.
-
Practice Regularly: The more you practice percentage calculations, the more comfortable and efficient you'll become.
-
Break Down Complex Problems: Large or complex percentage problems can often be broken down into smaller, more manageable steps.
-
Check Your Work: Always double-check your calculations to avoid errors.
Conclusion: Beyond the Calculation
While the answer to "What is 3 percent of 10000?" is definitively 300, the true value of this exercise lies in understanding the broader principles of percentage calculations and their wide-ranging applications. Mastering percentages is not just about solving mathematical problems; it’s about developing a crucial skillset for navigating various aspects of life, from personal finance to professional pursuits. This skill empowers informed decision-making, allowing you to analyze data effectively and participate more fully in the quantitative world around us. The ability to easily calculate percentages is a foundational skill that opens doors to understanding and engaging with a more complex world.
Latest Posts
Latest Posts
-
What Is 30 100 As A Percent
Apr 22, 2025
-
How To Find The Range In A Dot Plot
Apr 22, 2025
-
As Altitude Increases What Happens To Air Pressure
Apr 22, 2025
-
How Big Is 36 Inches In Cm
Apr 22, 2025
-
What Is 0 125 In A Fraction
Apr 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Percent Of 10000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.