What Is 3 To The 5 Power
Kalali
Jul 22, 2025 · 6 min read
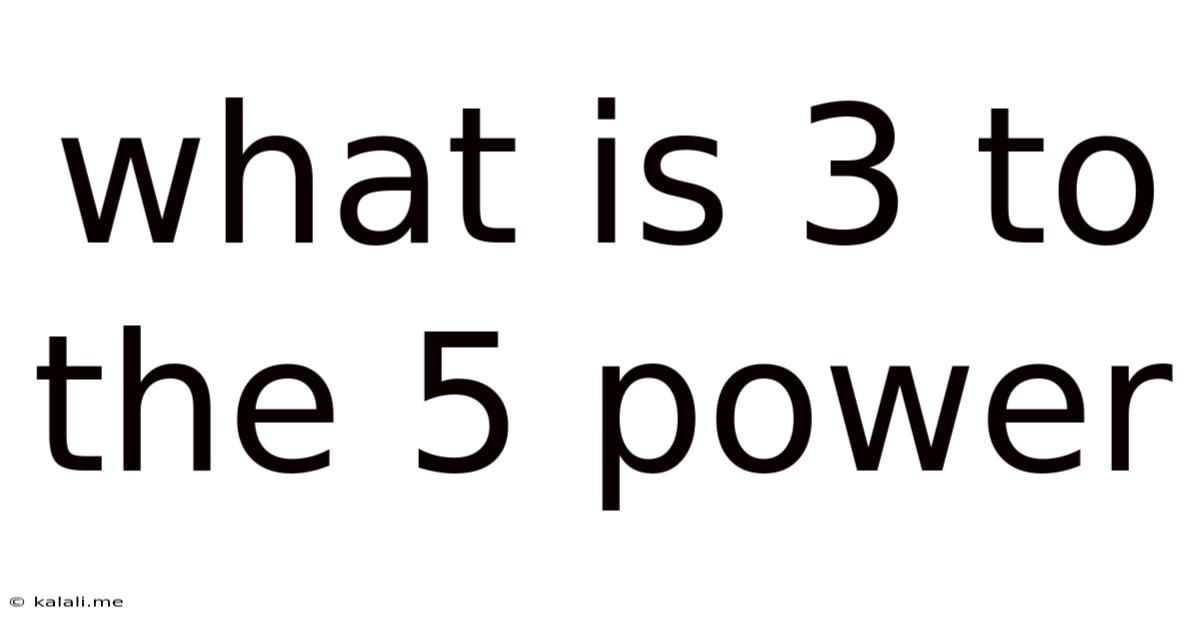
Table of Contents
What is 3 to the 5th Power? A Deep Dive into Exponents and Their Applications
What is 3 to the 5th power? At its simplest, it's a straightforward mathematical calculation: 3⁵ = 243. But this seemingly simple question opens a door to a vast world of mathematical concepts, including exponents, their properties, and their widespread applications in various fields. This article will explore 3⁵ in detail, examining the underlying principles of exponentiation, its practical uses, and how to tackle more complex exponent problems.
Understanding Exponents: A Foundation
Before delving into the specifics of 3⁵, let's solidify our understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. In the expression a<sup>b</sup>, 'a' is the base, and 'b' is the exponent. This expression signifies that 'a' is multiplied by itself 'b' times. For example:
- 2³ = 2 × 2 × 2 = 8
- 5² = 5 × 5 = 25
- 10¹ = 10
Therefore, 3⁵ means 3 multiplied by itself five times: 3 × 3 × 3 × 3 × 3 = 243. This seemingly simple calculation forms the bedrock for understanding more complex mathematical operations and models.
Calculating 3 to the 5th Power: Methods and Techniques
While simple multiplication suffices for 3⁵, understanding different calculation methods is crucial for handling larger exponents or more complex expressions. Here are a few approaches:
-
Direct Multiplication: This involves the straightforward method of multiplying the base number by itself the specified number of times. For 3⁵, this would be: 3 × 3 = 9; 9 × 3 = 27; 27 × 3 = 81; 81 × 3 = 243. This method is easy to understand but becomes cumbersome for larger exponents.
-
Using a Calculator: For larger exponents, a calculator significantly simplifies the process. Scientific calculators usually have an exponent function (often denoted as x<sup>y</sup> or ^). Simply input 3, press the exponent function, enter 5, and press equals to obtain the result: 243.
-
Logarithms (for advanced calculations): For incredibly large exponents, logarithms offer a more efficient calculation method. Logarithms essentially reverse exponentiation. While not necessary for 3⁵, understanding logarithms is beneficial for solving more intricate exponential equations.
Properties of Exponents: Expanding the Knowledge Base
Understanding the properties of exponents is essential for manipulating and simplifying exponential expressions. These properties enable us to solve complex problems efficiently. Here are some key properties:
-
Product of Powers: When multiplying two numbers with the same base, add the exponents: a<sup>m</sup> × a<sup>n</sup> = a<sup>m+n</sup>. For instance, 2² × 2³ = 2<sup>(2+3)</sup> = 2⁵ = 32.
-
Quotient of Powers: When dividing two numbers with the same base, subtract the exponents: a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>. For example, 5⁴ / 5² = 5<sup>(4-2)</sup> = 5² = 25.
-
Power of a Power: When raising a power to another power, multiply the exponents: (a<sup>m</sup>)<sup>n</sup> = a<sup>mn*</sup>. For example, (2³)⁴ = 2<sup>(3×4)</sup> = 2¹² = 4096.
-
Power of a Product: When raising a product to a power, distribute the exponent to each factor: (ab)<sup>n</sup> = a<sup>n</sup> b<sup>n</sup>. For example, (2 × 3)² = 2² × 3² = 4 × 9 = 36.
-
Power of a Quotient: Similarly, when raising a quotient to a power, distribute the exponent to both the numerator and denominator: (a/b)<sup>n</sup> = a<sup>n</sup> / b<sup>n</sup>. For example, (4/2)² = 4²/2² = 16/4 = 4.
Mastering these properties allows for efficient simplification and solution of more complex exponential equations.
Applications of Exponents: Beyond the Classroom
Exponents are not merely abstract mathematical concepts; they have significant practical applications across various fields:
-
Compound Interest: In finance, compound interest calculations heavily rely on exponents. The formula for compound interest involves exponential growth, where the principal amount grows exponentially over time.
-
Population Growth: Modeling population growth often utilizes exponential functions. The rate of population increase can be expressed as an exponential equation, allowing for predictions of future population sizes.
-
Radioactive Decay: Radioactive decay follows an exponential decay model. The half-life of a radioactive substance, the time it takes for half of the substance to decay, is defined using exponential functions.
-
Computer Science: Exponents are fundamental in computer science, particularly in algorithms and data structures. The efficiency of certain algorithms is often expressed using Big O notation, which involves exponential functions.
-
Physics: Many physical phenomena, including wave mechanics, quantum physics, and even the study of simple harmonic motion, leverage exponential functions to describe their behavior.
Solving More Complex Exponential Problems: Advanced Techniques
While 3⁵ is a relatively simple calculation, understanding the principles allows us to tackle more complex exponential problems:
Let's consider an example: Solve for x in the equation 2<sup>x</sup> = 16. We can solve this by recognizing that 16 is 2⁴. Therefore, 2<sup>x</sup> = 2⁴, implying x = 4.
A more complex example: Simplify (2³ × 2⁵) / 2². Using the properties of exponents, we can simplify this as follows:
- Combine the terms in the numerator: 2³ × 2⁵ = 2<sup>(3+5)</sup> = 2⁸.
- Now we have 2⁸ / 2². Using the quotient rule, we subtract the exponents: 2<sup>(8-2)</sup> = 2⁶ = 64.
These examples demonstrate how understanding the properties of exponents simplifies complex calculations and allows for efficient problem-solving.
Negative and Fractional Exponents: Expanding the Scope
The concept of exponents extends beyond positive integers. Negative exponents represent reciprocals, and fractional exponents represent roots.
-
Negative Exponents: a<sup>-n</sup> = 1 / a<sup>n</sup>. For example, 2⁻² = 1 / 2² = 1/4.
-
Fractional Exponents: a<sup>m/n</sup> = <sup>n</sup>√a<sup>m</sup>. For example, 8<sup>2/3</sup> = <sup>3</sup>√8² = (<sup>3</sup>√8)² = 2² = 4.
Understanding these extensions broadens our ability to solve a wider range of exponential problems and opens doors to more advanced mathematical concepts.
Conclusion: The Significance of Understanding 3 to the 5th Power
While the answer to "What is 3 to the 5th power?" is simply 243, the journey to finding that answer has uncovered a wealth of mathematical concepts and their practical applications. From the basic principles of exponents to their properties and diverse applications, understanding exponentiation is crucial for success in various fields. This article has provided a comprehensive overview, equipping you with the knowledge to tackle more complex exponential problems and appreciate the significance of this seemingly simple mathematical operation. By understanding the fundamental principles and properties, you can confidently approach and solve a wider array of mathematical problems, unlocking a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
What Happened To Jp In Hells Kitchen
Jul 22, 2025
-
How Much Is Half A Ton In Pounds
Jul 22, 2025
-
How Much Is 5 Millimeters In Inches
Jul 22, 2025
-
How To Write 50 As A Fraction
Jul 22, 2025
-
How Many Decades Are In A Century
Jul 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 To The 5 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.