What Is 30 Percent Of 100
Kalali
Mar 12, 2025 · 5 min read
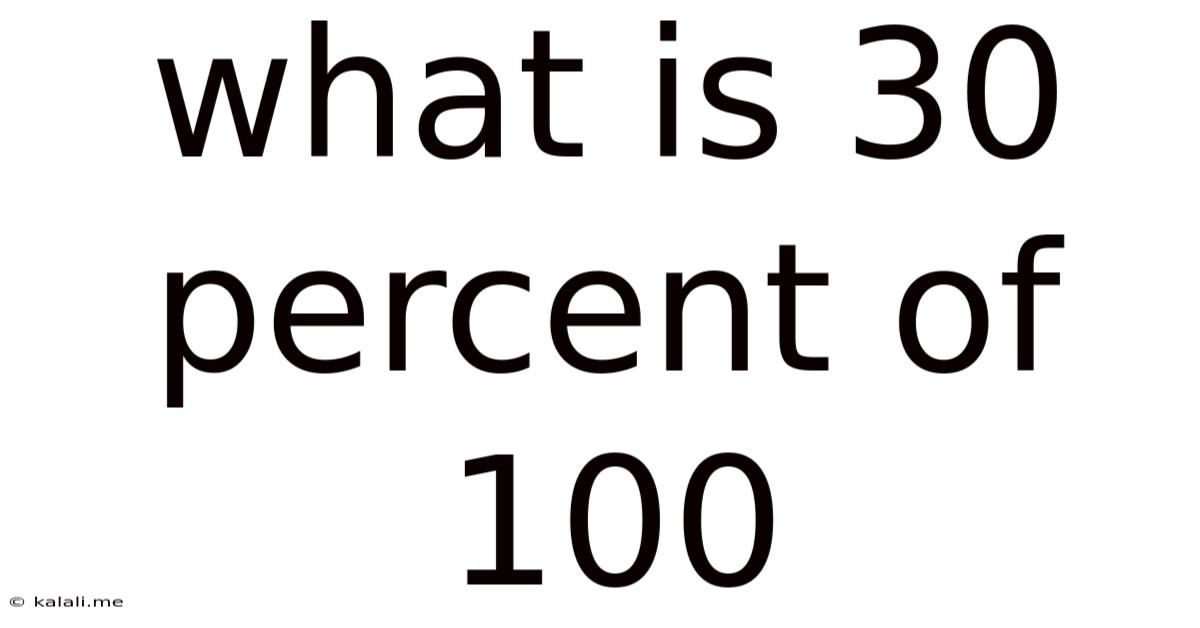
Table of Contents
What is 30 Percent of 100? A Deep Dive into Percentages and Their Applications
The question, "What is 30 percent of 100?" might seem simple at first glance. The answer, 30, is easily calculated. However, understanding the underlying concepts of percentages and their broad applications opens up a world of mathematical possibilities and practical uses across numerous fields. This article delves deep into the calculation, explores the meaning of percentages, and demonstrates their relevance in various real-world scenarios.
Understanding Percentages: The Building Blocks
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" (from the Latin per centum). This means 30% is equivalent to 30/100, or 3/10, or 0.3 as a decimal. Understanding this fundamental relationship is crucial to comprehending percentage calculations.
Key Concepts:
- The Whole: This is the total amount you're considering. In our example, the whole is 100.
- The Part: This is the portion of the whole that you're interested in finding. In our case, we want to find 30% of 100, so the part is what we are calculating.
- The Percentage: This is the rate or proportion expressed as a fraction of 100 (e.g., 30%).
Calculating 30% of 100: The Methods
There are several ways to calculate 30% of 100:
Method 1: Using the Fraction Method
This method directly applies the definition of percentage. Since 30% is equivalent to 30/100, we simply multiply this fraction by the whole (100):
(30/100) * 100 = 30
Method 2: Using the Decimal Method
Converting the percentage to a decimal makes the calculation straightforward. 30% is equivalent to 0.30 (or 0.3). Multiply this decimal by the whole:
0.3 * 100 = 30
Method 3: Using the Proportion Method
This method sets up a proportion:
30/100 = x/100
Solving for x (the part we want to find) gives us:
x = (30/100) * 100 = 30
Beyond the Basics: Real-World Applications of Percentages
The simple calculation of 30% of 100 serves as a foundation for countless real-world applications. Understanding percentages is essential in various fields, including:
1. Finance and Business:
-
Interest Rates: Banks and financial institutions use percentages to calculate interest on loans and savings accounts. Understanding compound interest, which involves calculating interest on both the principal and accumulated interest, requires a solid grasp of percentages. For example, calculating the interest earned on a savings account with a 3% annual interest rate involves percentage calculations.
-
Discounts and Sales: Retailers frequently advertise discounts using percentages (e.g., "30% off"). Calculating the final price after a discount requires understanding how to subtract a percentage from the original price. For example, a 30% discount on a $100 item would result in a $70 final price.
-
Profit Margins: Businesses use percentages to calculate their profit margins, representing the percentage of revenue that remains after deducting costs. This is crucial for understanding business profitability and making informed decisions.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages of income or purchase price. Calculating the total cost, including taxes, requires adding the tax percentage to the base amount.
2. Science and Statistics:
-
Data Analysis: Percentages are essential for presenting and interpreting data. For instance, scientists might express experimental results as percentages of a control group, allowing for easy comparison.
-
Probability and Statistics: Percentages are used to represent probabilities and statistical measures, such as the percentage of a population with a certain characteristic.
-
Scientific Measurements: In many scientific fields, measurements and changes are expressed as percentages, particularly when comparing changes over time or between different groups.
3. Everyday Life:
-
Tipping: Calculating a tip in a restaurant often involves determining a percentage (e.g., 15% or 20%) of the bill total.
-
Cooking and Baking: Recipes frequently involve percentages when scaling up or down, ensuring the proportions of ingredients remain consistent.
-
Shopping: Comparing prices and finding the best deals often necessitates understanding and comparing percentages of discounts and sales.
-
Health and Fitness: Tracking progress in fitness goals (e.g., weight loss or increase in strength) often involves calculating percentage changes over time.
Advanced Percentage Calculations: Beyond the Simple Example
While finding 30% of 100 is straightforward, more complex percentage problems require additional steps:
1. Finding the Percentage:
If you know the part and the whole, you can find the percentage by dividing the part by the whole and multiplying by 100:
Percentage = (Part / Whole) * 100
For example, if 30 is a part of 100, the percentage is: (30/100) * 100 = 30%
2. Finding the Whole:
If you know the part and the percentage, you can find the whole by dividing the part by the percentage (as a decimal):
Whole = Part / (Percentage / 100)
For example, if 30 is 30% of a whole, then the whole is: 30 / (30/100) = 100
3. Finding the Part Given Percentage Increase/Decrease:
Calculating percentage increases or decreases requires an understanding of how to add or subtract percentages from an initial value. For instance, a 10% increase on 100 would be 100 + (10/100)*100 = 110; a 10% decrease would be 100 - (10/100)*100 = 90.
4. Compound Percentage Changes:
This involves calculating percentage changes on a value that has already undergone a percentage change. This is common in financial calculations, like compound interest.
Conclusion: The Power and Versatility of Percentages
The seemingly simple question, "What is 30 percent of 100?" provides a gateway to understanding the fundamental concepts and widespread applications of percentages. From financial calculations and scientific data analysis to everyday tasks, percentages are an indispensable tool for making sense of numerical information and making informed decisions. Mastering percentage calculations equips you with a crucial skill that extends far beyond basic arithmetic. The ability to confidently manipulate and interpret percentages is a valuable asset in both professional and personal contexts. This article hopefully demystifies percentages and illustrates their practical relevance in a multitude of situations.
Latest Posts
Latest Posts
-
How Many Bunnies Are There In The World
Jun 30, 2025
-
How Is A Watch And Ruler Similar
Jun 30, 2025
-
How Many Liters Is In A Water Bottle
Jun 30, 2025
-
How Many Cups Of Milk Are In A Half Gallon
Jun 30, 2025
-
How Many Ritz Crackers In A Cup
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Percent Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.